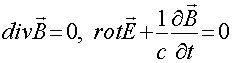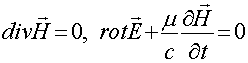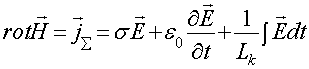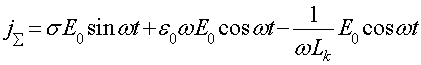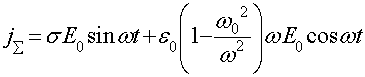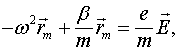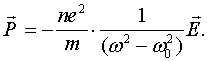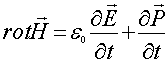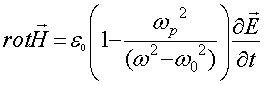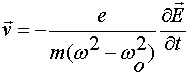Физические и методические ошибки в трудах Ландау и Гинзбурга
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
ВВЕДЕНИЕ
Сам создатель основных уравнений электродинамики Максвелл считал, что ни диэлектрическая, ни магнитная проницаемости от частоты не зависят, а являются фундаментальными константами. Как родилась идея дисперсии диэлектрической и магнитной проницаемости, и какой путь она прошла, достаточно красочно характеризует цитата из монографии хорошо известных специалистов в области физики плазмы [1]:
| |
Сам Дж. Максвелл при формулировке уравнений электродинамики материальных сред считал, что диэлектрическая и магнитная проницаемости являются постоянными величинами (по этой причине они длительное время считались постоянными величинами). Значительно позже, уже в начале этого столетия при объяснении оптических дисперсионных явлений (в частности явления радуги) Дж. Хевисайд и Р. Вул показали, что диэлектрическая и магнитная проницаемости являются функциями частоты. А совсем недавно, в середине 50-х годов, физики пришли к выводу, что эти величины зависят не только от частоты, но и от волнового вектора. По сути, это была радикальная ломка существующих представлений. Насколько серьезной она была, характеризует случай, который произошел на семинаре Л. Д. Ландау в 1954 г. Во время доклада А. И. Ахиезера на эту тему Ландау вдруг воскликнул, перебив докладчика: ”Это бред, поскольку показатель преломления не может быть функцией показателя преломления”. Заметьте, что это сказал Л. Д. Ландау – один из выдающихся физиков нашего времени. | |
Ниже мы покажем, что прав Максвелл, и диэлектрическая проницаемость материальных сред от частоты не зависит. В ряде же фундаментальных работ по электродинамике материальных сред [2-5] допущены методические и физические ошибки, в результате которых в физику проникло и прочно в ней закрепилось такое метафизические понятие, как частотная дисперсия диэлектрической проницаемости плазмы. Распространение этой концепции на диэлектрики привело к тому, что все начали считать, что и диэлектрическая проницаемость диэлектриков тоже зависит от частоты. Эти физические заблуждения проникли во все сферы физики и техники и прочно в ней закрепились.
ГДЕ ОШИБЛИСЬ ЛАНДАУ, ГИНЗБУРГ, АХИЕЗЕР И ТАММ
Прежде чем начать рассмотрение этого вопроса, мы должны дать официальную трактовку по поводу того, что в настоящее время называют уравнениями Максвелла.
Для этого обратимся к монографии известного специалиста в области электродинамики [6], и дадим выдержку из этой монографии без всяких купюр. На странице 204 читаем:
Таким образом, материальные уравнения Максвелла для рассмотренного случая приобретают вид:
(3)
(4)
Посмотрим на второе уравнение системы (3). Видно, что в его правой части имеются только две составляющие тока. Активная составляющая, обусловленная активной проводимостью
(5)
и реактивная проводимость, представляющая емкостной ток, или как его принято называть ток смещения.
На этой точке замерзания и просуществовали уравнения Максвелла со времени их написания автором.
Если считать, что в рассматриваемом пространстве отсутствуют не скомпенсированные заряды, то дивергенция в соотношении (3) тоже будет равна нулю.
Перепишем эти уравнения в системе СИ, опустив дивергенции.
(6)
(7)
Соотношение (7) можно переписать и по-другому. Поскольку два члена, стоящие в правой части соотношения (7) представляют собой плотности токов проводимости и смещения, то мы можем записать суммарный ток:
(8),
где
(9)
представляет активную плотность тока, ответственную за тепловые потери, а
(10)
представляет реактивный ток, который Максвелл назвал током смещения, и который подобен току, протекающему в емкости в элементах с сосредоточенными параметрами.
В таком убогом виде и просуществовали материальные уравнения Максвелла (6-7) вплоть до появления работ [7-10] .На мысль о модификации уравнения (7) навело то обстоятельство, что в нём не был учтён тот факт, что, например, в сверхпроводниках заряды могут двигаться вообще без трения. Плотность тока для этого случая может быть найдена из уравнения движения свободно движущегося электрона.
(11)
где ![]() и
и ![]() масса и заряд электрона. Если учесть плотность электронов
масса и заряд электрона. Если учесть плотность электронов ![]() , то для плотности тока сразу получаем
, то для плотности тока сразу получаем
(12)
где
(13)
кинетическая индуктивность свободных электронов.
Видно, что плотность тока, определяемая соотношением (12), представляет индуктивный ток, подобный тому, как это имеет место в индуктивности в цепях с сосредоточенными параметрами.
Если представить все три плотности тока в виде векторной диаграммы, то подобно тому, как это имеет место в цепях с сосредоточенными параметрами, мы получим три вектора. При этом индуктивный ток будет отставать от активного на 90 градусов, а ёмкостной ток буде опережать активный на такую же величину.
Таким образом, второе уравнение Максвелла принимает следующий вид:
(14)
Обратим внимание на то, что в таком явном виде уравнение Максвелла для проводников до появления работ [7,8], никто не записывал.
Если сделать замены  ,
, ![]() ,
, ![]() а
а ![]() , то мы получим ток, протекающий через параллельный резонансный контур, состоящий из параллельно включенных емкости, индуктивности и проводимости, к которому приложено напряжение
, то мы получим ток, протекающий через параллельный резонансный контур, состоящий из параллельно включенных емкости, индуктивности и проводимости, к которому приложено напряжение ![]() . Вот почему мы говорим, что процессы, протекающие в цепях с сосредоточенными параметрами полностью эквивалентны процессам в материальных среда. При этом, конечно, такое соответствие имеет место только тогда, когда можно пренебречь пространственными вариациями напряжённости электрического поля.
. Вот почему мы говорим, что процессы, протекающие в цепях с сосредоточенными параметрами полностью эквивалентны процессам в материальных среда. При этом, конечно, такое соответствие имеет место только тогда, когда можно пренебречь пространственными вариациями напряжённости электрического поля.
Из соотношения (14) видно, что так точно, как и в резонансном параллельном контуре в материальной среде, являющейся проводником, течет три вида токов: активный, емкостной и индуктивный. Соотношение (14) годится для описания всех возможных временных спектров прикладываемых к среде электрических полей, включая и постоянный ток, а также переменные поля, начиная от гармонических, и кончая полями с любой их зависимостью от времени. Единственным условием является возможность их дифференцирования и интегрирования.
Физики привыкли для решения физических задач пользоваться комплексным представлением. Но это лишь один частный случай, когда речь идёт о гармонических полях. Если же закономерность зависимости полей от времени другая то, чтобы использовать комплексный метод, необходимо раскладывать эти поля в ряд Фурье. В этом ограниченность указанного метода. В соотношении (14) этих ограничений нет.
Если к соотношению (14) добавить первое уравнение Максвелла, то мы поучим вещественные уравнения для проводников, описывающее все возможные процессы, протекающие в проводниках:
(15)
Укажем, что возможности этой системы уравнений гораздо шире, чем, если бы мы записали её в комплексном представлении. Например, из неё сразу следуют феноменологические уравнения сверхпроводящего состояния – уравнения Лондонов. Из этих уравнений сразу, при определённых граничных условиях, следует такое новое физическое явление, как поперечный плазменный резонанс в незамагниченной плазме [ 9-11] .
Для гармонических полей система уравнений (15) описывает плоскую электромагнитную волну. И вот на этом этапе рассмотрения Ландау, Гинзбург, Ахиезер и Тамм делают грубую терминологическую и физическую ошибку, которая способствовала внедрению в физику метафизического понятия диспергирующей (зависящей от частоты) диэлектрической проницаемости проводников (плазмы) (ДДПП). В чём она заключается?
Будем считать, что электрическое поле меняется по гармоническому закону.
(16)
Тогда второе уравнение системы (15) можно переписать следующим образом:
(17)
Обратите внимание, что последние два члена соотношения (17) описываются одной и той же временной функцией. Однако, в связи с тем, что перед последним членом правой части стоит знак минус, ясно, что фазы этих составляющих плотностей токов сдвинуты на 180 градусов. И это вполне естественно, т.к., так точно как и в элементах с сосредоточенными параметрами, ёмкостной и индуктивный ток всегда сдвинуты на 180 градусов. Если взять единичный объем рассматриваемой среды и провести аналогию с параллельным колебательным контуром, то можно заключить, что резонансная частота такого контура ![]() будет определяться соотношением
будет определяться соотношением
(18)
Делая с учётом соотношения (18) соответствующие преобразования в (17), получаем
(19)
И вот, наконец, указанные учёные объявляют величину
(20)
диспергирующей диэлектрической проницаемостью плазмы [2-5].
Но в электродинамике диэлектрическая проницаемость вводиться только в диэлектриках на основании вполне детерминированных процедур при помощи введения вектора поляризации, который предполагает наличие градиентов плотности зарядов. Но, как показано в работе того же Ахиезера [4], при распространении плоской волны, описываемой соотношениями (15) в проводящей среде отсутствуют градиенты пространственного заряда.
Заметим, что таким точно образом мы могли бы ввести и другое метафизическое понятие, а именно, диспергирующую кинетическую индуктивность
(21)
где
(22)
Конечно соотношения (20) и (22) никакого отношения к физическим понятиям диэлектрической проницаемости или индуктивности не имеют. Это сборные параметры, которые представляют комбинацию физических величин, которые действительно представляют такие физические величины, как диэлектрическая проницаемость вакуума и удельная кинетическая индуктивность носителей зарядов, и эти величины от частоты не зависят.
В чем опасность такой терминологической ошибки, связанной с подменой понятий. Она заключается, прежде всего, в том, что в сознании нескольких поколений физиков укоренилось устойчивое метафизическое мировоззрение о том, что такой физический параметр как диэлектрическая проницаемость может зависеть от частоты. И главная беда в том, что эту ошибочную точку зрения они пытаются перенести и на диэлектрики, искренне веря в то, что и диэлектрическая проницаемость диэлектриков может зависеть от частоты. Если сейчас спросить любого физика, зависит ли диэлектрическая проницаемость диэлектрика от частоты, каждый ответит, что зависит. В этом и кроется основное заблуждение и опасность, которые внедрили в физику Ландау, Гинзбург и их последователи. На эти мои слова все физики также единодушно ответят, что я несу полнейшую чепуху, т.к. явный пример с преломляющими способностями призмы ни о чём другом свидетельствовать не может, как о зависимости диэлектрической проницаемости от частоты. Я долго воздерживался от этих слов, но всё-таки должен их сейчас произнести. Большего преступления перед физикой, как внедрение в умы целых поколений физиков таких понятий и, в частности, понятия дисперсии материальных параметров придумать трудно. Я думаю, что это одно из величайших заблуждений физики за последнее столетие.
Что происходит с проводящими средами, и что частотная дисперсия распространения ЭМ волн обусловлена обоюдным действием двух не зависящих от частоты физических параметров: диэлектрической проницаемости вакуума и кинетической индуктивности носителей зарядов я думаю уже все поняли.
А как же обстоят дела с диэлектриками. Наличие в диэлектриках связанных зарядов, представляющих атомы и молекулы самого диэлектрика, приводит при наложении на них электрических полей к образованию микроскопических электрических диполей, а, следовательно, и вектора поляризации. На поляризацию затрачивается дополнительная энергия, которая отбирается у источника поля, и, таким образом, в диэлектрике накапливается дополнительная потенциальная энергия.
Как формировались наши взгляды на свойства диэлектриков в переменных полях? Начало было положено геометрической оптикой, когда феноменологическим образом было введено понятие коэффициента преломления и оптической плотности сред. Значительную роль в процессе изучения прозрачных сред сыграли законы Снелиуса, при помощи которых можно вычислить углы преломления и отражения. Однако, до появления классической электродинамики и уравнений Максвелла истинного понимания процессов, сопутствующих этим явлениям не было. Электродинамические процессы, происходящие в диэлектриках, достаточно разнообразны и для их рассмотрения понадобилась не одна статья. Поэтому в данном случае мы начнём с простейшей задачи об электронной поляризации в диэлектриках.
В этом случае отдельный атом или молекула может быть представлены как механический осциллятор, когда заряд, имеющий массу, под воздействием электрических сил осуществляет колебательное движение около центра масс атома или молекулы. В этом случае отклонение поляризуемых зарядов от положения равновесия определяется величиной электрического поля и коэффициентом упругости ![]() , характеризующего упругость сил связи зарядов в атомах и молекулах. Эти величины связаны соотношением
, характеризующего упругость сил связи зарядов в атомах и молекулах. Эти величины связаны соотношением
(23)
где ![]() – отклонение зарядов от положения равновесия.
– отклонение зарядов от положения равновесия.
Обозначая резонансную частоту связанных зарядов через ![]() , и учитывая, что
, и учитывая, что
(24)
из (23) получаем
(25)
Мы видим, что в соотношении (25) уже присутствует частота и масса, причем отклонение заряда от положения равновесия обратно пропорционально массе. Это говорит о том, что инерционные свойства колеблющихся зарядов также будут влиять на колебательные процессы поляризуемых атомов и молекул. С этим и связана зависимость величины вектора поляризации от частоты электрического поля. Поэтому мы введем частотозависимый вектор поляризации,
(26)
Видно, что при соблюдении условия ![]() вектор поляризации стремится к бесконечности. Это означает наличие резонанса на этой частоте.
вектор поляризации стремится к бесконечности. Это означает наличие резонанса на этой частоте.
Поскольку электрическая индукция определяется соотношением
(27)
То второе уравнение Максвелла приобретает вид:
(28)
или
(29)
Мы видим, что в выражении (29) снова появилась кинетическая индуктивность зарядов, участвующих в колебательном процессе:
(30)
С учётом этого соотношение (29) можно переписать
(31)
или
(32)
или
(33)
или
(34)
где
(35)
плазменная частота зарядов, входящих в состав атомов или молекул диэлектрика, в том случае, если эти заряды были бы свободны. Такой результат вполне ожидаем, т.к. колеблющиеся связанные заряды тоже имеют массу, а, следовательно, и кинетическую индуктивность.
Интересно, что такой точно результат мы можем получить вообще не вводя такого мало понятного физического понятия как вектор поляризации, который даже Ландау ввел в заблуждение. Это можно сделать, правильно записав плотности токов просто вычисляя плотности токов. Кстати этим методом мы уже пользовались, когда рассматривали процессы в проводниках. Рассматриваемые нами молекулы или атомы находятся в вакууме. Правда, у читателей может возникнуть вопрос, о каком вакууме может идти речь, если имеется твердое тело. Ответ на этот вопрос прост. В этом случае плотность атомов или молекул очень высока, но, всё равно они находятся в вакууме. Запишем суммарную плотность тока как сумму плотностей тока смещения и тока проводимости:
(36)
Воспользовавшись соотношением (25) для нахождения скорости колеблющихся зарядов, получим
(37)
Подставляя это выражение в соотношение (36), получаем
(38)
И далее, используя соотношение (35) запишем
(39)
Соотношения (34) и (39) полностью совпадают. Проделав эти преобразования, мы показали некоторую искусственность введения такого понятия, как вектор поляризации. Просто для любой мыслимой модели нужно правильно уметь вычислять плотности токов, входящих во второе уравнение Максвелла вот и всё.
И, конечно же, у нас опять возникает большой соблазн назвать величину, стоящую перед производной в соотношениях (34) и (39), диспергирующей (частотозависимой) диэлектрической проницаемостью диэлектрика (ДДПД). Но правильное ли такое определение? Такое определение, как и в случае ДДПП неверно, т.к. указанный параметр опять является сборным и в него входят теперь уже сразу три не зависящих от частоты параметра.
Мы видим, что в соотношения (34) и (39) входят две характерные частоты ![]() и
и ![]() . Частота
. Частота ![]() , назовём её собственной, является индивидуальной характеристикой атома или молекулы и от их плотности заполнения пространства не зависит. При таком утверждении мы предполагаем, что в пространстве они расположении на таком расстоянии, что их влияние друг на друга отсутствует, т.е. они настолько удалены друг от друга, что электрические и магнитные поля, окружающих родственных или других атомов или молекул не влияют на указанную резонансную частоту. Напротив,
, назовём её собственной, является индивидуальной характеристикой атома или молекулы и от их плотности заполнения пространства не зависит. При таком утверждении мы предполагаем, что в пространстве они расположении на таком расстоянии, что их влияние друг на друга отсутствует, т.е. они настолько удалены друг от друга, что электрические и магнитные поля, окружающих родственных или других атомов или молекул не влияют на указанную резонансную частоту. Напротив, ![]() зависит от плотности атомов и молекул, входящих в состав диэлектрика. И здесь возникает очень интересный вопрос, а что если в его состав входят различные группы разнородных атомов и молекул? Ответ напрашивается сам собой. В этом случае каждая такая группа будет характеризоваться собственной резонансной частотой, плазменная же частота указанной группы будет характеризоваться её парциальной плотностью атомов или молекул. Теперь мы можем представить, какое разнообразие различных резонансов может наблюдаться в многокомпонентных системах. Этим и определяется то разнообразие красок, которое мы видим вокруг, поскольку на резонансных частотах происходит максимальное отражение или поглощение сигнала заданной частоты электромагнитных колебаний, чем выделяется заданный цвет видимого нами объекта. И чем чище мы видим свет, например, в рубине или сапфире, тем добротнее тот резонанс атома или молекулы, частоту которого мы наблюдаем.
зависит от плотности атомов и молекул, входящих в состав диэлектрика. И здесь возникает очень интересный вопрос, а что если в его состав входят различные группы разнородных атомов и молекул? Ответ напрашивается сам собой. В этом случае каждая такая группа будет характеризоваться собственной резонансной частотой, плазменная же частота указанной группы будет характеризоваться её парциальной плотностью атомов или молекул. Теперь мы можем представить, какое разнообразие различных резонансов может наблюдаться в многокомпонентных системах. Этим и определяется то разнообразие красок, которое мы видим вокруг, поскольку на резонансных частотах происходит максимальное отражение или поглощение сигнала заданной частоты электромагнитных колебаний, чем выделяется заданный цвет видимого нами объекта. И чем чище мы видим свет, например, в рубине или сапфире, тем добротнее тот резонанс атома или молекулы, частоту которого мы наблюдаем.
Рассмотрим два предельных случая:
Если ![]() значительно меньше
значительно меньше ![]() то из (34) получаем
то из (34) получаем
(40)
В этом случае коэффициент, стоящий перед производной, от частоты не зависит, и представляет статическую диэлектрическую проницаемость диэлектрика. Как видим она зависит от собственной частоты колебаний и от плазменной частоты. Этот результат понятен. Частота в данном случае оказывается настолько малой, что инерционные свойства зарядов не сказываются и величина вектора поляризации практически достигает максимальных статических значений. С точки зрения эквивалентных схем единичный объём такого диэлектрика представляет ёмкость, величина которой равна коэффициенту, стоящему перед производной в соотношении (36). Из формулы (40) мы можем сделать ещё один очевидный вывод. Чем жестче связи в атоме или молекуле, т.е. чем выше собственная частота ![]() , тем меньше статическая диэлектрическая проницаемость. В то же время, чем больше их плотность в пространстве, тем выше статическая диэлектрическая проницаемость. Вот вам сразу и рецепт для создания диэлектриков с максимальной диэлектрической проницаемостью. Что бы достичь этого, следует в заданном объёме пространства упаковать максимальное количество молекул с максимально мягкими связями.
Очень показательным является случай, когда
, тем меньше статическая диэлектрическая проницаемость. В то же время, чем больше их плотность в пространстве, тем выше статическая диэлектрическая проницаемость. Вот вам сразу и рецепт для создания диэлектриков с максимальной диэлектрической проницаемостью. Что бы достичь этого, следует в заданном объёме пространства упаковать максимальное количество молекул с максимально мягкими связями.
Очень показательным является случай, когда ![]() значительно меньше
значительно меньше ![]() . Тогда
. Тогда
(41)
и на наших глазах диэлектрик превратился в проводник (плазму) т.к. полученное соотношение в точности совпадает со случаем плазмы. Именно это совпадение и натолкнуло Ландау на мысль, что нет никакой разницы между поведением плазмы и поведением диэлектриков на очень высоких частотах. Однако, это не так. Действительно на очень высоких частотах в диэлектриках ввиду инерционности зарядов их амплитуда колебаний очень мала и вектор поляризации тоже мал. В то же время, как в плазме он всегда тождественно равен нулю, независимо от частоты колебаний.
Заметим, что данное рассмотрение показало, что такой параметр как кинетическая индуктивность зарядов характеризует любые колебательные процессы зарядов независимо от того свободные они или связанные. Он имеет такое же фундаментальное значение, как диэлектрическая и магнитная проницаемость среды. Почему он до сих пор не был замечен, и почему ему не было отведено должное место. Это опять таки связано с тем, что физики привыкли мыслить математическими категориями, не сильно вникая в суть самих физических процессов.
Из соотношения (24) видно, что в случае выполнения равенства ![]() амплитуда колебаний равна бесконечности. Это означает наличие резонанса в этой точке. Бесконечная амплитуда колебаний получается по причине того, что мы не учитывали потерь в резонансной системе, в связи с чем её добротность равна бесконечности. В каком-то приближении мы можем считать, что ниже указанной точки мы имеем дело с диэлектриком, у которого диэлектрическая проницаемость равна её статическому значению. Выше этой точки мы имеем дело уже фактически с металлом, у которого плотность носителей тока равна плотности атомов или молекул в диэлектрике.
амплитуда колебаний равна бесконечности. Это означает наличие резонанса в этой точке. Бесконечная амплитуда колебаний получается по причине того, что мы не учитывали потерь в резонансной системе, в связи с чем её добротность равна бесконечности. В каком-то приближении мы можем считать, что ниже указанной точки мы имеем дело с диэлектриком, у которого диэлектрическая проницаемость равна её статическому значению. Выше этой точки мы имеем дело уже фактически с металлом, у которого плотность носителей тока равна плотности атомов или молекул в диэлектрике.
И вот теперь пришла очередь ответить на вопрос, почему призма разлагает полихроматический свет на монохроматические составляющие. В свете полученных результатов ответ на этот вопрос очень прост. Для того чтобы это имело место необходимо иметь частотную зависимость фазовой скорости (дисперсию) электромагнитных волн в рассматриваемой среде. Если к соотношению (34) добавить первое уравнение Максвелла
(42)
(43)
То из соотношения (43) легко найти волновое уравнение. Для среды, в которой отсутствуют свободные заряды, получаем:
(44)
Если учесть, что
(45),
то уже ни у кого не останется сомнения в том, что при распространении электромагнитных волн в рассмотренном диэлектрике будет наблюдаться их частотная дисперсия. Но эта дисперсия будет связана не с тем, что такой материальный параметр как диэлектрическая проницаемость зависит от частоты, а в формировании такой дисперсии будет принимать участие сразу три физические величины, а именно: собственная резонансная частота самих атомов или молекул, плазменная частота зарядов, если считать их свободными, и диэлектрическая проницаемость вакуума.
Как мы уже указали коэффициент, стоящий перед производной в правой части соотношения (43) не является диэлектрической проницаемостью рассмотренной среды, а, как и в случае с плазмой, представляет реактивную проводимость диэлектрика. Причём эта проводимость, в зависимости от частоты, может носить как ёмкостной, так и индуктивный характер.
Поэтому дисперсионные свойства диэлектриков обусловлены двумя не зависящими от частоты параметрами: статической диэлектрической проницаемостью диэлектриков и кинетической индуктивностью, которой обладают, как оказывается, не только свободные, но и связанные заряды. Ведь при наличии в среде диэлектрика переменных электрических полей даже связанные заряды осуществляют колебательное движение, а поскольку при этом они имеют переменную скорость, то их кинетические свойства оказывают самое непосредственное влияние на процессы распространения ЭМ волн. С точки зрения эквивалентной схемы оказывается, что диэлектрик, в отличие от проводника, представляет не параллельный, а последовательный колебательный контур, со всеми вытекающими из этого последствиями. И если проводник или плазма это унылая тоталитарная система, где все подчинены одному единому правилу, и все частицы находятся в одном и том же энергетическом состоянии, то диэлектрик это совсем иное состояние. Каждый резонирующий атом это индивидуум. И если бы все, атомы, входящие в состав диэлектрика имели бы разные резонансные частоты, то столько бы резонансов мы и наблюдали. В реальной ситуации в состав диэлектрика входят только несколько групп атомов и молекул. И каждая из этих групп имеет свой резонанс. Более того, сила такого резонанса определяется процентным (парциальным) количеством резонирующих молекул. Чем их больше, тем сильнее резонанс. Вот откуда берётся та цветовая гамма, которую мы наблюдаем вокруг. До чего же всё просто и в то же время непросто, т.к. такие простые вещи до сих пор физики понять не могут. И значительная часть вины в этом лежит на Ландау. Конечно, никто не спорит, что он был блестящим математиком, но наша беда заключается в том, что он из математических законов начал выводить физические законы, а не наоборот. Вот и получили мы таким способом в своё распоряжение частотную дисперсию материальных параметров.
Нельзя не отметить и ещё один важный вопрос. Мы всегда считали, что единственными физическими параметрами, которые определяют все электродинамические характеристики материальных сред, являются диэлектрическая и магнитная проницаемости. Сейчас мы начинаем понимать, что у этих физических величин появился третий равноправный партнёр, которым является кинетическая индуктивность зарядов, из которых состоят все материальные среды. И ни один процесс взаимодействия электромагнитных полей с материальными средами не может без него обойтись.
СПИСОК ЛИТЕРАТУРЫ
- 1. Александров А. Ф., Богданкевич Л. С., Рухадзе А. А. Колебания и волны в плазменных средах. Изд. Московского университета, 1990.- 272 с.
- 2. Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. М: Физматгиз, 1973.- 454 с.
- 3. Гинзбург В. Л. Распространение электромагнитных волн в плазме. М.: Наука. 1967 г. - 684 с.
- 4. Ахиезер А. И. Физика плазмы. М: Наука, 1974 – 719 с.
- 5. Тамм И. Е. Основы теории электричества. М.: Наука, 1989 – 504 с.
- 6. Дж. Джексон. Классическая электродинамика М.: Мир,1965 – 702 с.
- 7. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с. ISBN 966-7983-55-2.
- 8. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 9. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 10. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 11. Transversal plasma resonance in a nonmagnetized plasma and possibilities of practical employment of it. arXiv, physics/0506081.