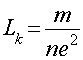О модификации уравнений Лондонов

Федор Федорович Менде
Дата рождения:	02.07.1939 г.
Гражданство:
Учёная степень:	доктор технических наук
Сайт:	http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0

Уравнения Лондонов являются основными феноменологическими уравнениям, которые до сих пор используют для электродинамического описания сверхпроводников [1]. Напомним, как они были получены. Первое уравнение

(1)

где

(2)

есть лондоновская глубина проникновения. В этом соотношении принято: - магнитная проницаемость вакуума, а , и - масса, величина заряда и их плотность соответственно.

Уравнение (1) было получено в предположении того, что заряды в сверхпроводнике являются свободными и их движение подчиняется закону

(3)

Из уравнений Максвелла, которые для случая сверхпроводника Лондоны записали следующим образом:

(4)

(5)

они получили уравнение для магнитного поля:

(6)

Далее, уже не из электродинамических, а из термодинамических соображений, на основе опытов Мейснера, Лондоны в уравнении (6) меняют производную на постоянное поле и получают следующее уравнение:

(7)

Замена производной на постоянное поле была произведена на основании того, что опыты Мейснера показали, что при переходе материала, находящегося в магнитном поле, в сверхпроводящее состояние это поле из материала выталкивается. Это обстоятельство связано с тем, что всякая система стремится к минимуму свободной энергии. Поскольку свободная энергия образца при наличии магнитного поля больше, чем при его отсутствии, то и происходит выталкивание магнитного поля. С математической точки зрения это явление можно учесть, полагая константу, получающуюся при интегрировании уравнения (6) равной нулю.

Уравнения (1) и (7), которые принято называть уравнениями Лондонов, в таком виде и просуществовали вплоть до появления работы [2].

Если мы посмотрим на то, как записали Лондоны второе уравнение Максвелла (см. соотношение (5)), то мы можем заметить, что в нём не хватает тока смещения. С учётом этого обстоятельства полная система уравнений Максвелла, описывающая поведение сверхпроводников, как в переменных, так и постоянных полях должна быть записана следующим образом:

(8)

(9)

После несложных преобразований с учётом (1) получаем

(10)

(11)

где

(12)

есть кинетическая индуктивность зарядов, представляющих сверхпроводящие носители зарядов. А уравнения (10) и (11) являются феноменологическими электродинамическими уравнениями, описывающими поведение сверхпроводников как в переменных так и в постоянных полях. Из этих уравнений следуют также и уравнения Лондонов.

Такой подход открывает одну интересную особенность распространения электромагнитных волн в средах, где заряды могут считаться свободными или квазисвободными. К таким средам относятся не только сверхпроводники, но и потоки заряженных частиц, а также горячая разреженная плазма.

Оказывается, что учёт только электрических и магнитных полей при рассмотрении в таких системах этих полей недостаточен. Это связано с тем, что удельная энергия, накопленная в рассматриваемых материальных средах, теперь определяется уже не только электрическими и магнитными полями. Энергия в этом случае накапливается и в кинетическом движении самих зарядов. Полная энергия в данном случае записывается как

(13)

где , и есть амплитуды полей и плотности тока.

Следует отметить, что до появления работы [2] в таком явном виде полную энергию никто не записывал. В связи с тем, что в энергии появился дополнительный член, такие волны уже не могут называться чисто электромагнитными, а должны быть названы электромагнитнокинетическими волнами.

Последний член в соотношении (13) можно записать и через электрическое поле:

(14)

где

(15)

плазменная частота, её ещё называют частотой ленгмюровских колебаний.

До сих пор эта частота вводилась как частота продольных колебаний в незамагниченной плазме. Но уравнения (10-11) представляют распространение поперечных электромагнитных волн. В чем здесь дело. Как показано в работе [2], это означает, что в незамагниченной плазме при определённых условиях может иметь место также поперечный плазменный резонанс.

Всё это означает, что в результате плохого понимания физических явлений, происходящих в рассмотренных средах, до появления работы [2] оставалось незамеченным целое научно-техническое направление.

Литература

• 1. Менде Ф. Ф., Спицын А. И. Поверхностный импеданс сверхпроводников. Киев, Наукова думка, 1985.- 240 с.
• 2. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с. ISBN 966-7983-55-2