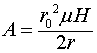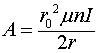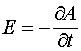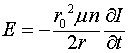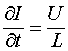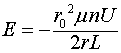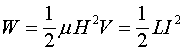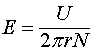Ошибочность экспериментов Аронова-Бома
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Векторный потенциал появляется в уравнении Шредингера и он не может быть заменён магнитным полем и этот факт был очевиден с момента написания этого уравнения.
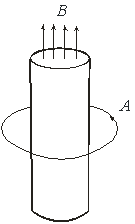
Эксперимент Ааронова-Бома [1—3] был задуман для того, чтобы доказать влияние магнитного потенциала при отсутствии магнитного поля на электронную интерференцию. Идея состояла в том, чтобы ввести между электронными траекториями магнитную нить или тонкий соленоид, ортогональный к траекториям и достаточно длинный, так, чтобы магнитное поле его концов, не могло изменять электронные траектории. Основополагающим предположением такого эксперимента является то утверждение, что вокруг длинного соленоида существуют линии векторного потенциала, в то время как магнитное поле в этих областях отсутствует. Приведём по этому поводу рисунок из шестого тома Фейнмановских лекций [4].
Рис. 1. Магнитное поле и векторный потенциал длинного соленоида.
При таком рассмотрении предполагается, что вокруг длинного соленоида существует векторный потенциал, а магнитное поле отсутствует. Связь между векторным потенциалом и магнитным полем определяется из равенства
Если считать, что ![]() - радиус соленоида, а
- радиус соленоида, а ![]() - расстояние от оси соленоида до точки, где определяется векторный потенциал, то связь между магнитным полем в соленоиде и векторным потенциалом запишется:
- расстояние от оси соленоида до точки, где определяется векторный потенциал, то связь между магнитным полем в соленоиде и векторным потенциалом запишется:
Отсюда получаем
(1)
В длинном соленоиде магнитное поле равно удельному току ![]() , приходящемуся на единицу длины соленоида
, приходящемуся на единицу длины соленоида
(2)
где ![]() - ток, текущий через соленоид, а
- ток, текущий через соленоид, а ![]() - количество витков, приходящееся на единицу длины соленоида.
- количество витков, приходящееся на единицу длины соленоида.
Подставляя (2) в (1), получаем:
(3)
Поскольку
из (3) получаем
(4)
Если к соленоиду, имеющему индуктивность ![]() подключить источник напряжения
подключить источник напряжения ![]() , то производная тока, текущего через соленоид запишется:
, то производная тока, текущего через соленоид запишется:
(5)
Из (4) и (5) получаем
(6)
Энергия магнитного поля соленоида определяется соотношением
(7)
где ![]() - объём, занимаемый магнитными полями соленоида.
- объём, занимаемый магнитными полями соленоида.
При большой длине соленоида полями рассеяния на его концах можно пренебречь и считать, что
(8)
Из (7) и (8) получаем
(9)
Подставляя (9) в (6), находим
(10)
где ![]() есть общее число витков соленоида.
есть общее число витков соленоида.
Соотношение (10) говорит о том, что в момент подключения источника питания к соленоиду, мгновенно вокруг него возникает электрическое поле. Причём характерной особенностью этого поля является то, что оно от времени не зависит. Ещё одной особенностью такого поля является то, что оно не обладает энергией, т.к. при расчёте энергии, накопленной в соленоиде, учитываются только магнитные поля внутри самого соленоида. Естественно токая версию возникновения и характеристик такого поля принята быть не может. Но поскольку это поле является следствием существования рассмотренного векторного потенциала, то и рассмотренная версия возникновения векторного потенциала вокруг длинного соленоида тоже не может быть принята.
Ошибочность проведенного рассмотрения векторного потенциала вокруг длинного соленоида исходит из того предположения, что ток во всех витках длинного соленоида изменяется синхронно во всех его частях. Но такое представление означает возможность передачи информации вдоль такого соленоида с бесконечной скоростью, что противоречит всем известным фактам.
Теория длинных линий, в которых поля распространяются с конечной скоростью, хорошо разработана. Если длинный соленоид необходимо подключить к источнику напряжения, то для этого необходим не только сам соленоид, но и обратный провод. Поэтому такая система превращается в длинную линию, в которой ток по соленоиду распространяется с конечной скоростью, постепенно заполняя сам соленоид магнитным полем. Этот вопрос подробно рассмотрен в работах [5, 6].
Но тогда спрашивается, что же измерили в своих экспериментах Аронов и Бом? Скорее всего, в их экспериментах были допущены какие-то ошибки. Ошибка могла заключаться в том, что ферромагнитный цилиндр, который они использовали в качестве соленоида, был намагничен неоднородно или имел разную толщину воль длины. Это могло привести к наличию магнитного поля в окрестностях цилиндра, что они и измерили.
Список литературы
- 1. Aharonov Y., Bohm D. Physical Review, 1959. V. 115. Р. 85.
- 2. Olariu S., Iovitsu Popescu I. Reviews of Modern Physics, 1985. V. 57. № 2. Р. 339—436.
- 3. Tonomura A. The Quantum World Unveiled by Electron Waves, with a Preface of Chen Ning Yang, World Scientific, Singapore, 1998.
- 4. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.
- 5. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 6. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.