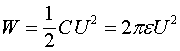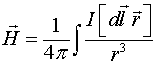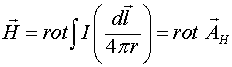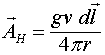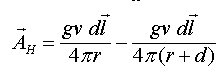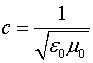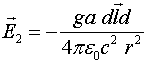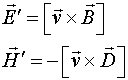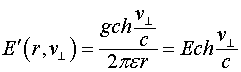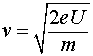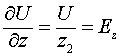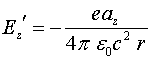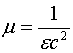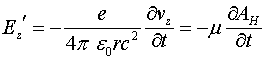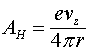Как излучает антенна
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Феноменологическое описание излучающих свойств антенны
Начнём рассмотрение вопроса с опытов Герца. Именно работа его антенны в свободном колебательном режиме проливает свет на многие физические процессы её работы. Если имеется уединённый проводящий шар, то его ёмкость определяется соотношением
где ![]() - диэлектрическая проницаемость окружающей среды, а
- диэлектрическая проницаемость окружающей среды, а ![]() – радиус шара.
– радиус шара.
Электрическое поле такого шара обладает энергией
Именно эту энергию и сообщал Герц шарам своей антенны, заряжая их от источника высокого напряжения. Суперпозиция полей этих зарядов, которые представляют электрический диполь, и представляют основную часть полей ближней зоны антенны. Эти поля убывают, в зависимости от направления, обратно пропорционально квадрату и кубу расстояния. Но они же в рассматриваемом случае представляют и ту начальную энергию, которая в будущем будет в режиме свободных колебаний превращена в поля излучения. Указанные поля, являясь энергетической копилкой антенны, никакого отношения к полям излучения не имеют.
Если соединить заряженные шары при помощи проволоки, то заряды начнут перетекать с одного шара на другой, пытаясь обнулить разность потенциалов, которая между ними имеется. Но поскольку проводник, их соединяющий, имеет индуктивность, то в этой цепи, предстваляющей колебательный контур, начнётся колебательный процесс, при котором будет происходить периодическая перезарядка шаров. И если бы не было омических потерь в проводниках и потерь на излучение, то этот процесс продолжался бы бесконечно долго, причём частота колебаний определялась бы ёмкостью шаров и индуктивностью проводника, их соединяющего. Но если измерить электрические и магнитные поля вблизи такого колебательного контура, то окажется что сдвиг фаз между ними близок к ![]() , т.е. такие поля представляют реактивный процесс, при котором вектор Пойнтинга является реактивным. Это означает, что энергия, запасённая в колебательном контуре, не может его покинуть.
, т.е. такие поля представляют реактивный процесс, при котором вектор Пойнтинга является реактивным. Это означает, что энергия, запасённая в колебательном контуре, не может его покинуть.
Шары, разряжаясь через проводник, заставляют заряды двигаться, причём, поскольку это движение периодическое, они движутся с периодическим ускорением. Т.е. та энергия, которая ранее была запасена в статических полях шаров, заставляет двигаться заряды в проводнике, их соединяющем, с переменным ускорением.
Теперь рассмотрим то явление, которое хорошо изучено с феноменологической точки зрения, но физика которого до сих пор не ясна. Речь пойдёт об электрических полях индукции. Хорошо известно, что если к проводнику, по которому течёт переменный ток, поднести другой проводник, то в этом проводнике возникнут наведенные токи, направление которых будет обратным тем токам, которые текут в исходном проводнике. Наша задача заключается в том, чтобы найти те механизмы, которые приводят к излучению антенной энергии в виде ЭМ волн, и путь к этому пониманию лежит через выяснение роли электрических полей индукции в этом процессе. Мы пока не будем вдаваться в физическую природу их появления, этот вопрос мы рассмотрим позже. Отметим лишь тот факт, что поля индукции появляются только в том случае, когда в проводниках имеет место ускорение зарядов. Процесс протекает следующим образом. Чтобы ускорить заряды в проводнике необходимо наличие электрического поля. Это поле обеспечивает разность потенциалов на рассматриваемых сферах, а периодичность этого поля обеспечивает колебательный процесс в колебательном контуре. Но если электрические поля, ускоряющие заряды, имеются в самом проводнике, то поля индукции, направленные против ускоряющих полей имеются не только в проводнике, но и снаружи самого проводника. Но на создание внешних полей индукции требуется энергия, поскольку любое электрическое поле обладает удельной энергией равной
И получается так, что, расходуя энергию, накопленную в электрическом диполе на ускорение зарядов в проводнике, соединяющем сферы, создаётся энергия полей индукции вне этого проводника. Но сами поля индукции, и это следует из свойств векторного потенциала, являющегося следствием закона Био и Савара, обладают важным свойством, они убывают по закону ![]() , что соответствует законам излучения. Рассмотрим этот вопрос подробнее.
, что соответствует законам излучения. Рассмотрим этот вопрос подробнее.
Магнитное поле в своё время было введено Ампером феноменологическим путём на основе наблюдения силового взаимодействия между проводниками, по которым течёт ток. Закон Био и Савара (его тоже иногда называют законом Ампера), выраженный в векторной форме, определяет магнитное поле в точке наблюдения в следующем виде:
где ![]() - ток в элементе
- ток в элементе ![]() ,
, ![]() - вектор, направленный из
- вектор, направленный из ![]() в точку наблюдения (рис. 1).
в точку наблюдения (рис. 1).
Рис. 1. Формирование векторного потенциала элементом проводника ![]() , по которому течёт ток
, по которому течёт ток ![]() .
.
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
векторный потенциал магнитного поля.
Замечательным свойством этого выражения является то, что зависимость векторного потенциал обратно пропорциональна расстоянию до точки наблюдения, что характерно для законов излучения.
Поскольку ![]() , где
, где ![]() количество зарядов, приходящееся на единицу длины проводника, из (1.1) получаем:
количество зарядов, приходящееся на единицу длины проводника, из (1.1) получаем:
Если размер элемента ![]() , по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом
, по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом ![]() , по которому течёт ток
, по которому течёт ток ![]() имеет вид
имеет вид
(1.2)
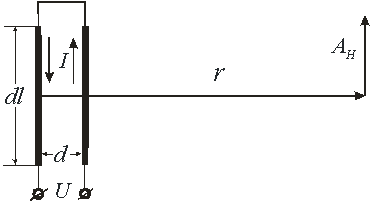
Из этого соотношения следует интересный факт. Даже на постоянном токе зависимость векторного потенциала от расстояния соответствует законам излучения. И, казалось бы, что, меняя скачками ток в коротком отрезке провода, и измеряя векторный потенциал в удалённой точке, можно передавать информацию в эту точку по законам излучения. Но этому мешает то обстоятельство, что цепь постоянного тока всегда замкнута на локальный источник питания и поэтому всегда есть как прямой, так и обратный провод. Эта особенность приводит к тому, что скалярный потенциал в дальней зоне оказывается обратно пропорционален квадрату расстояния до наблюдаемой точки. Это легко показать на примере двух параллельных элементов проводника, расположенных на расстоянии ![]() (рис. 2), в которых текут встречные токи.
(рис. 2), в которых текут встречные токи.
В этом случае векторный потенциал в удалённой зоне определяется как сумма векторных потенциалов, создаваемых в дальней зоне каждым токовым элементом в отдельности.
Рис. 2. Формирование векторного потенциала двумя параллельными участками проводников, по которым текут встречные токи.
(1.3)
Поскольку
(1.4)
где ![]() - магнитная проницаемость вакуума, из (1.2) и (1.3) получаем:
- магнитная проницаемость вакуума, из (1.2) и (1.3) получаем:
(1.5)
для случая, изображенного на рис. 1.
(1.6)
для случая, изображенного на рис. 2. В этих соотношениях  - ускорение зарядов.
- ускорение зарядов.
Из уравнений Максвелла известно, что поля электромагнитных волн распространяются в свободном пространстве со скоростью
где ![]() - диэлектрическая проницаемость вакуума. Если учесть это соотношение, то равенства (1.5) и (1.6) можно переписать:
- диэлектрическая проницаемость вакуума. Если учесть это соотношение, то равенства (1.5) и (1.6) можно переписать:
Если имеется точечный заряд ![]() , то эти соотношения принимают вид:
, то эти соотношения принимают вид:
Эти поля обладают и вторым важным свойством. Они распространяются в пространстве со скоростью света.
Таким образом, накопленная в контуре энергия, заключённая в полях ближней зоны, ускоряя заряды в проводнике, и создавая тем самым поля индукции, превращается в поля излучения. Возникает вопрос, а можно ли создать реальную систему, состоящую из генератора и проводников, которая обеспечивала излучение ЭМ волн. Как это сделать легко понять из рис. 2. Нужно обеспечить такое расстояние между проводниками, чтобы запаздывание полей индукции было равно половине периода. При таком запаздывании поля обоих излучателей окажутся в месте расположения каждого излучателя синфазными, а следовательно произойдёт их сложение и эта синфазность будет наблюдаться во всём пространстве интерференции полей.
Теперь выясним, при каких условиях такая антенна будет максимально эффективно излучать накопленную в ней энергию. Известно, что у электромагнитной волны в свободном пространстве отношение электрического поля к магнитному равно волновому сопротивлению свободного пространства, которое составляет 377 Ом. Антенна будет согласована со свободным пространством в том случае, когда на поверхности её проводников отношение электрического поля индукции и магнитного поля текущего по проводникам тока также будет равно 377 Ом. Для этого необходимо, чтобы характеристическое сопротивление резонансного контура (корень квадратный из отношения индуктивности к ёмкости контура), которым является антенна, было равно 377 Ом. Для того чтобы соблюсти это условие в полуволновом вибраторе подбирают соответствующую длину трубок, регулируя тем самым его ёмкость, и толщину трубок, регулируя его индуктивность.
До сих пор мы рассматривали ЭМ излучение антенны в свободном режиме. При этом выяснили, что это излучение происходит на её резонансной частоте. Что нужно сделать, чтобы антенна могла излучать в непрерывном режиме? Очевидно, необходимо при помощи линии питания подводить к ней ту энергию, которую антенна теряет на омические потери и излучение. Делают это при помощи подводящей линии, но волновое сопротивление линию тоже нужно согласовать с характеристическим сопротивлением резонансного контура антенны. Делается это известным способом при помощи трансформатора.
Что будет, если мы будем работать не на резонансной частоте, а начнём сдвигаться от резонанса по частоте в ту или иную сторону. Если начнём сдвигаться в область более низких частот, та антенна уже не будет представлять для линии чисто активную нагрузку, а появится дополнительная индуктивная составляющая. Если будем сдвигаться вверх – появится дополнительная ёмкостная составляющая. На такую нагрузку генератор работает плохо, т.к. часть энергии будет отражаться от антенны. Для того чтобы избежать этого, реактивности компенсируют подключением к антенне соответствующих обратных реактивностей. Эта операция, равноценна настройке антенного резонансного контура на заданную частоту.
Таким образом, в ближней зоне антенны имеется одновременно и суперпозиционные дипольные поля и поля излучения. Чтобы определить их удельный вес, нужно измерить в интересующем месте электрическое и магнитное поле и сдвиг фаз между ними, а затем вычислить активную и реактивную составляющие. Активная составляющая даст поля электромагнитной волны, а реактивная, суперпозиционные поля.
Даже специалисты по антенной технике не могут объяснить, почему тонкий провод антенны может собирать энергию волны из большом пространства её окружающего. Рассмотрим, как взаимодействует электрический заряд с электрическим полем обычного конденсатора. Если нарисовать суперпозицию полей конденсатора и полей заряда, то видно, что в очень большом пространстве вокруг заряда создаются градиенты полей, которые и заставляют двигаться заряд вместе с его полями к одной из пластин конденсатора. Таким образом, сам точечный заряд и его поля это та единая конструкция, которая заставляет сам заряд взаимодействовать с окружающими полями. Теперь разместим параллельно полям конденсатора электрический диполь и опять нарисуем суперпозицию полей конденсатора и диполя. Опять окажется, что области полей, где образуются их градиенты, занимают обширные области вокруг зарядов. Именно эти градиенты и будут оказывать силовое действия на заряды, заставляя их сближаться или удаляться в зависимости от направления внешнего электрического поля. Для увеличения расстояния между зарядами необходимо затрачивать работу, и эту работу будут совершать поля конденсатора во всей зоне их взаимодействия с полями диполя. Сразу заметим, что поля электрического диполя это так называемые поля ближней зоны антенны. Именно в этой зоне и отбирает энергию электрический диполь, образующийся в антенне, у полей электромагнитной волны. Сам процесс отбора антенной энергии происходит следующим образом. При наложении на неё электрического поля волны начинает образовываться электрический диполь, поля которого и взаимодействуют с полем волны, отбирая у неё энергию. И отбор этой энергии происходит во всей ближней зоне, т.к. именно в ближней зоне в результате интерференции создаются градиенты полей, которые заставляют разводить заряды в проводниках антенны. Разведённые же заряды создают э.д.с. на её зажимах. В случае же отсутствия активной нагрузки у антенны происходит переизлучение электрических полей, падающих на её ближнюю зону. При этом поля антенны сначала создают колеблющийся электрический диполь, а уже этот диполь излучает волны в соответствии с законами излучения. Поэтому ближняя зона является тем собирателем энергии электромагнитных волн из пространства, которая затем тратиться или в полезной нагрузке, или переизлучается в свободное пространство.
Физические причины возникновения векторного потенциала магнитного поля
Как мы установили, феноменологические свойства векторного потенциала проливают свет на процессы излучения. Однако до сих пор была не ясна физическая причина возникновения такого потенциала.
Поля, которые создаются в данной инерциальной системе отсчёта (ИСО) движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
В классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной [1].
В данном разделе будет сделана попытка найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [2-5], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы записываются следующим образом:
(2.1)
или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [4]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [4]. Электрическое поле 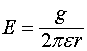 за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом:
(2.4)
где ![]() - скалярный потенциал неподвижного заряда. Потенциал
- скалярный потенциал неподвижного заряда. Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
Если волновое сопротивление линии равно ![]() и к ней подключить источник постоянного напряжения (рис 3), в ней начнет распространяться волна тока
и к ней подключить источник постоянного напряжения (рис 3), в ней начнет распространяться волна тока 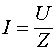 и напряжения
и напряжения ![]() . Волна тока в правой своей части имеет переходной участок
. Волна тока в правой своей части имеет переходной участок ![]() , который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса
, который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса 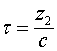 , за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
, за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
Рис. 3. Распространение волны тока и напряжения в длинной линии.
Именно на этом переходном участке и происходит ускорение зарядов от нулевой скорости в его начале, до значений необходимых для создания номинального тока в линии, величина которого определяется соотношением 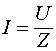 . К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Интервал
. К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Интервал ![]() соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что
соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что ![]() >>
>>![]() .
.
На этом рисунке фронт волны занимает отрезок линии длинной ![]() , следовательно, время такого переходного процесса равно
, следовательно, время такого переходного процесса равно  . Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время
. Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время ![]() достигает своего максимального значения
достигает своего максимального значения ![]() , после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок
, после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок ![]() . Изобразим этот участок отдельно, как показано на рис. 4.
. Изобразим этот участок отдельно, как показано на рис. 4.
Рис. 4. Фронт волны тока, распространяющейся в длинной линии
На участке ![]() происходит ускорение зарядов от их нулевой скорости (правее участка
происходит ускорение зарядов от их нулевой скорости (правее участка ![]() ) до значения скорости, определяемого соотношением
) до значения скорости, определяемого соотношением
где ![]() и
и ![]() - заряд и масса носителей тока, а
- заряд и масса носителей тока, а ![]() - падение напряжения на участке
- падение напряжения на участке ![]() . Тогда зависимость скорости носителей тока от координаты будет иметь вид:
. Тогда зависимость скорости носителей тока от координаты будет иметь вид:
(2.5)
Поскольку мы приняли линейную зависимость напряжения от времени на входе линии, то имеет место равенство
где ![]() - напряженность поля, ускоряющая заряды на участке
- напряженность поля, ускоряющая заряды на участке ![]() . Следовательно, соотношение (2.5) мы можем переписать
. Следовательно, соотношение (2.5) мы можем переписать
Теперь, используя соотношение (2.4) для величины скалярно-векторного потенциала, вычислим его значение как функцию ![]() на некотором расстоянии
на некотором расстоянии ![]() от линии
от линии
(2.6)
При записи соотношения (2.6) использованы только первые два члена разложения в ряд, функции, определяемой соотношением (2.4).
Пользуясь формулой ![]() , и продифференцировав соотношение (2.6) по
, и продифференцировав соотношение (2.6) по ![]() , получаем
, получаем
(2.7)
где ![]() - электрическое поле, индуцируемое на расстоянии
- электрическое поле, индуцируемое на расстоянии ![]() от проводника линии. Около
от проводника линии. Около ![]() мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружаюших линию проводниках индукционные токи, противоположные по направлению тем, которые текут в индуцирующей линии. Ускорение
мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружаюших линию проводниках индукционные токи, противоположные по направлению тем, которые текут в индуцирующей линии. Ускорение ![]() , испытуемое зарядом
, испытуемое зарядом ![]() в поле
в поле ![]() , определяется соотношением
, определяется соотношением  . С учетом этого из (2.7) получаем
. С учетом этого из (2.7) получаем
(2.8)
Таким образом, заряды, ускоряемые в отрезке линии ![]() , индуцируют на расстоянии
, индуцируют на расстоянии ![]() от этого участка электрическое поле, определяемое соотношением (2.8). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Таким образом, получен закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Но это соотношение полностью совпадает с равенством (1.5), которое получено феноменологическим путём на основе введения векторного потенциала магнитного поля, если учесть, что
от этого участка электрическое поле, определяемое соотношением (2.8). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Таким образом, получен закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Но это соотношение полностью совпадает с равенством (1.5), которое получено феноменологическим путём на основе введения векторного потенциала магнитного поля, если учесть, что
Этот закон можно называть законом электро-электрической индукции, так как он, минуя поля посредники (магниное поле или векторный потенциал), дает прямой ответ на то, какие электрические поля генерирует вокруг себя ускоряемый электрический заряд. Именно это соотношение, а не закон Фарадея, мы должны считать основным законом индукции, т.к. именно оно устанавливает причину появления индукционных электрических полей вокруг движущегося заряда. В чем заключается разница между предлагаемым подходом и ранее существующим. Ранее говорилось, что движущийся заряд генерирует векторный потенциал, а уже изменяющийся векторный потенциал генерирует электрическое поле. Соотношение (2.8) дает возможность исключить эту промежуточную операцию и перейти непосредственно от свойств движущегося заряда к индукционным полям. Из соотношению (2.8) следует и введенный ранее феноменологическим путем векторный потенциал, а следовательно, и магнитное поле. Равенство (2.8) можно переписать
откуда, интегрируя по времени, получаем
Это соотношение полностью соответствует определению векторного потенциала. Теперь видно, что векторный потенциал есть прямое следствие зависимости скалярного потенциала от скорости. Введение и векторного потенциала и магнитного поля это всего лишь полезный математический приём, который позволяет упростить решение ряда электродинамических задач, однако, следует помнить, что первоосновой введение этих полей является скалярно-векторный потенциал.
Список литературы
- 1. Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967, - 664 - с.
- 2. Менде Ф. Ф. К вопросу об уточнении уравнений электромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 3. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с.
- 4. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 5. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.