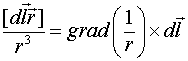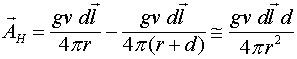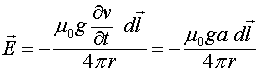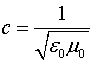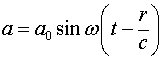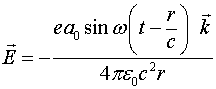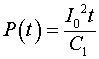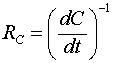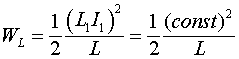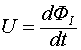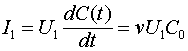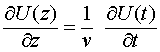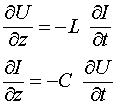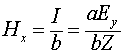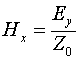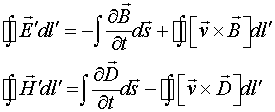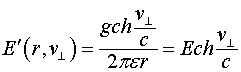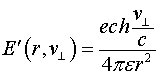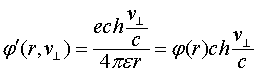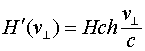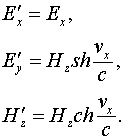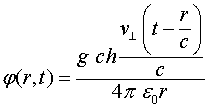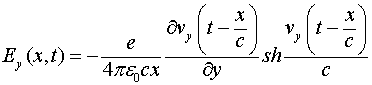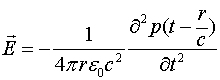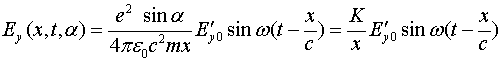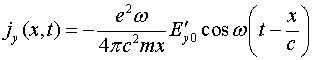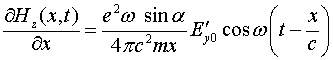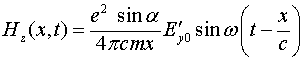Излучение и особенности распространения электромагнитных волн
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
Одним из самых загадочных явлений в электродинамике являются излучение и распространение электромагнитных волн. Никто до сих пор не понимает как это происходит. Приведём по этому поводу цитату из шестого тома Фейнмановских лекций по физике «Электродинамика»:
«Я просил вас представить себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно делать? И как я сам представляю себе электрическое поле? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытку представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку.
Чтоб получить представление об электромагнитном поле, требуется более высокая степень воображения. Почему? Да потому что для того, чтобы невидимые ангелы стали доступны пониманию, мне нужно только чуть-чуть изменить их свойства – я делаю их слегка видимыми, и тогда уже могу увидеть и форму их крыльев, их тела, их нимбы. Как только мне удастся представить видимого ангела, то необходимая для дальнейшего абстракция (состоящая в том, что почти невидимых ангелов представить себе совершенно невидимыми) оказывается сравнительно лёгким делом. Вы можете тоже сказать: «Профессор, дайте мне, пожалуйста, приближенное описание электромагнитных волн, пусть даже слегка неточное, на такое, чтобы я смог увидеть их так, как я могу увидеть почти невидимых ангелов, и я видоизменю эту картину до нужной абстракции».
Увы, я не могу это сделать для вас. Я просто не знаю как. У меня нет картины этого электромагнитного поля, которая была бы хоть в какой-то степени точной. Я узнал об электромагнитном поле давным-давно, 25 лет тому назад, когда я был на вашем месте, и у меня на 25 лет больше опыта размышлений об этих колеблющихся волнах. Когда я начинаю описывать магнитное поле, движущееся через пространство, то говорю о полях Е и В, делаю руками волнистые движения и вы можете подумать, что я способен их видеть. А на самом деле, что я при этом вижу? Вижу какие-то смутные, туманные, волнистые линии, на них там и сям написано Е и В, а у других линий имеются словно какие-то стрелки, то здесь, то там на них есть стрелки, которые исчезают, едва в них вглядишься. Когда я рассказываю о полях, проносящихся сквозь пространство, в моей голове катастрофически перепутываются символы, нужные для описания объектов и сами объекты. Я не в состоянии дать картину, хотя бы приблизительно похожую на настоящие волны. Так что, если вы сталкиваетесь с такими же затруднениями при попытках представить поле, не терзайтесь, дело обычное». (конец цитаты). О чём говорит это признание известного физика, курс лекций которого является одним из лучших курсов по физике. Он говорит о том, что до настоящего времени не было чёткого представления о происхождении и распространении электромагнитных волн. Впрочем, и вся классическая электродинамика находится примерно в таком же состоянии, когда для объяснения электродинамических явлений приходится применять различного рода постулаты, начиная от постулата о силе Лоренца и кончая постулатами СТО.
Так всё же, можно построить такую электродинамику и такую картину электромагнитных волн, которую можно было бы представить человеку немного знающему физику. Попытаемся это сделать.
Концепция излучения в классической электродинамике
Начнём с энергетических характеристик электрического поля. Во-первых, любое поле это такое поле, которое можно обнаружить при помощи измерительных приборов. Если имеется заряженный плоский конденсатор, состоящий из двух плоских пластин, то электрическое поле между ними легко обнаружить, вводя между этими пластинами пробный заряд. По силе, действующей на такой заряд, и обнаруживается электрическое поле. Характерным свойством такого поля является то, что оно представляет непрерывную однородную среду, обладающую удельной энергией, пропорциональной квадрату электрического поля. В этом легко убедится при помощи простого эксперимента. Если начать раздвигать пластины конденсатора ( рис. 1), то при этом будет необходимо затрать определённую работу.
Рис. 1. Конденсатор, состоящий из плоскопараллельных заряженных пластин.
Если поверхностная плотность зарядов на его пластинах равна ![]() , то напряженность электрического поля между его пластинами равна
, то напряженность электрического поля между его пластинами равна
Без учёта краевых эффектов электрическая сила, действующая на пластины конденсатора определяется соотношением
Если при этом пластины раздвинуть на расстояние ![]() ,, то при этом будет совершена механическая работа
,, то при этом будет совершена механическая работа
Но энергия электрических полей тоже будет равна этой же величине. Если же пластины сближаются, то, наоборот, электрическая энергия будет превращаться в механическую. Эти примеры показывает, как механическая энергия превращается в электрическую и наоборот.
Если заставить через пространство лететь электрические поля, подобные тем, которые имеют место в рассмотренном конденсаторе, то эти поля будут нести на себе энергию и это будет способ передачи энергии на расстояние посредством электрических полей.
Хорошо известно, что вблизи проводов, по которым течёт переменный электрический ток, образуются электрические поля индукции, которые могут быть связаны с переменным магнитным полем. Магнитное поле в своё время было введено Ампером феноменологическим путём на основе наблюдения силового взаимодействия между проводниками, по которым течёт ток. Закон Ампера, выраженный в векторной форме, определяет магнитное поле в точке наблюдения в следующем виде:
где ![]() , - ток в элементе
, - ток в элементе ![]() ,,
,, ![]() , - вектор, направленный из
, - вектор, направленный из ![]() в точку наблюдения (рис. 2).
в точку наблюдения (рис. 2).
Можно показать, что
и, кроме того, что
Рис. 2. Формирование векторного потенциала элементом проводника ![]() , по которому течёт ток
, по которому течёт ток ![]() .
.
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
где
(1.1)
Замечательным свойством этого выражения является то, что зависимость векторного потенциал обратно пропорциональна расстоянию до точки наблюдения. Именно это свойство и позволяет получить законы излучения.
Поскольку ![]() , где
, где ![]() количество зарядов, приходящееся на единицу длины проводника, из (1) получаем:
количество зарядов, приходящееся на единицу длины проводника, из (1) получаем:
Если размер элемента ![]() , по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то это соотношение имеет вид:
, по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то это соотношение имеет вид:
Из этого соотношения следует интересный факт. Даже на постоянном токе зависимость векторного потенциала от расстояния соответствует законам излучения. И, казалось бы, что, меняя скачками ток в коротком отрезке провода, и измеряя векторный потенциал в удалённой точке, можно передавать информацию в эту точку по законам излучения. Но этому мешает то обстоятельство, что цепь постоянного тока всегда замкнута на локальный источник питания и поэтому всегда есть как прямой, так и обратный провод. Эта особенность приводит к тому, что скалярный потенциал в дальней зоне оказывается обратно пропорционален квадрату расстояния до наблюдаемой точки. Это легко показать на примере двух параллельных элементов проводника, расположенных на расстоянии ![]() (рис. 3), в которых текут встречные токи.
(рис. 3), в которых текут встречные токи.
Рис. 3. Формирование векторного потенциала двумя параллельными участками цепи, по которым течёт встречный ток.
В этом случае векторный потенциал в удалённой зоне определяется как сумма векторных потенциалов, создаваемых в дальней зоне каждым токовым элементом в отдельности. При условии ![]() значительно больше
значительно больше ![]() получаем:
получаем:
Избежать этих трудностей можно путём использования переменных токов. Поскольку электрическое поле и векторный потенциал в свободном пространстве связаны соотношением
где ![]() - магнитная проницаемость вакуума, то электрическое поле, создаваемое в дальней зоне элементом тока
- магнитная проницаемость вакуума, то электрическое поле, создаваемое в дальней зоне элементом тока ![]() будет зависеть от ускорения зарядов в этом элементе
будет зависеть от ускорения зарядов в этом элементе
(1.2)
где ![]() - ускорение зарядов. Из уравнений Максвелла известно, что электрические поля распространяются в свободном пространстве со скоростью
- ускорение зарядов. Из уравнений Максвелла известно, что электрические поля распространяются в свободном пространстве со скоростью
(1.3)
где ![]() - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
Поэтому, если токовые элементы расположить на расстоянии равном половине длины волны и создать в них разнонаправленные токи, то в дальней зоне за счёт запаздывания электрические поля от отдельных токовых элементов сложатся, и суммарное электрическое поле удвоится:
Если в соотношении (1.2) учесть, что поля распространяются с конечной скоростью и учесть запаздывание  , то с учётом соотношения (1.3) получим:
, то с учётом соотношения (1.3) получим:
(1.4)
В том случае, когда ускорение зарядов меняется по гармоническому закону
соотношение (1.4) принимает вид
(1.5)
В случае, когда размер элемента тока значительно меньше расстояния до точки наблюдения, получаем:
(1.6)
Соотношения (1.4-1.6) показывает, что волны электрического поля в свободном пространстве распространяются с конечной скоростью. Рассматривая электрические поля плоского конденсатора, мы видели, что такие поля обладают удельной энергией, которую и будут переносить при своём распространении.
Но в таком рассмотрении мет места магнитному полю, которое имеется в электромагнитной волне. Такое поле может быть введено как чисто математическое поле из второго уравнения Максвелла
Или для случая малости элемента тока по сравнению с расстоянием до точки наблюдения
(1.7)
Из этих соотношений следует, что магнитное поле является пространственной производной электрического поля.
Если имеется одиночный заряд ![]() , то соотношения (1.6) и (1.7) перепишутся следующим образом:
, то соотношения (1.6) и (1.7) перепишутся следующим образом:
(1.8)
(1.9)
где ![]() - единичный вектор в направлении движения заряда.
- единичный вектор в направлении движения заряда.
Запишем эти соотношения в декартовой системе координат, считая, что направлением распространения является ось ![]() , а вектор
, а вектор ![]() направлен по оси
направлен по оси ![]() (рис. 4).
(рис. 4).
Рис. 4. Схема формирования магнитного поля.
Из соотношения (1.9) получаем
(1.10)
При интегрировании этого соотношения следует учесть, что при длине волны значительно меньшей, чем расстояние до точки наблюдения, гармоническая производная по координате значительно больше, чем производная от обратного значения координаты. Поэтому координату в числителе правой части соотношения (1.10) можно считать постоянной величиной. При этом условии из соотношения (1.10) получаем
(1.11)
Это значение магнитного поля получено при условии существованию компоненты электрического поля
(1.12)
Разделив (1.12) на (1.11) получаем
где ![]() - волновое сопротивление вакуума.
- волновое сопротивление вакуума.
Проведенное рассмотрение показало, что в свободном пространстве может распространяться так называемая электромагнитная волна, у которой векторы электрического и магнитного поля синфазны. Подчеркнём ещё раз, что введение вектора магнитного поля является чисто математической формальностью, которая не является необходимой для построения теории излучения.
Таким образом, опираясь на феноменологическую концепцию магнитного поля, получены законы распространения электромагнитных волн. Эти законы исключают необходимость использования уравнений Максвелла, т.к. из них могут быть получены все законы распространения, а уравнения Максвелла по отношению к этим уравнениям являются частным случаем, когда расстояние от излучателя до точки наблюдения велико.
Остаётся только спросить, почему электродинамика не пошла по этому пути сразу же после введения понятия магнитного поля. Ответ кроется в том, что тогда никто не знал о существовании электромагнитных волн и только уравнения Максвелла и опыты Герца подтвердили это.
Таким образом, с феноменологией всё ясно, но физическая основа такого подхода нам не ясна, т.к. совершенно не понятно, что с физической точки зрения представляет векторный потенциал и почему он связан с движением зарядов. В связи с непониманием этих вопросов, а векторный потенциал является ответственным не только за излучение, но и за силовое взаимодействия токонесущих систем, классическая электродинамика и разделена до настоящего времени на две не связанные друг с другом части. Одна её часть это уравнения Максвелла, определяющие волновые процессы в материальных средах. Другая часть, определяющая силовое взаимодействие токонесущих систем, основывается на экспериментальном постулате о силе Лоренца.
Из соотношений (8) и (11) видно, что электрические и магнитные поля электромагнитных волн в такой постановке вопроса зависят только от вторых производных координаты по времени, и в данном случае пока нет ответа по поводу того, могут ли эти поля зависеть от более высоких производных.
Дальнейшее развитие феноменологических подходов к вопросам распространения электромагнитных волн
Законы самоиндукции
К законам самоиндукции следует отнести те законы, которые описывают реакцию таких элементов радиотехнических цепей, как ёмкость, индуктивность и сопротивление при гальваническом подключении к ним источников тока или напряжения. Эти законы являются основой теории электрических цепей. Движение зарядов в какой-либо цепи связано с потреблением энергии от источников питания, которые заставляют их менять своё местоположение или двигаться. Процессы взаимодействия источников питания с такими структурами регулируются законами самоиндукции.
К самоиндукции отнесём также тот случай, когда при наличии подключенного источника питания или накопленной в системе энергии могут меняться ее параметры. Такую самоиндукцию будем называть параметрической. В дальнейшем будем использовать такие понятия: как генератор тока и генератор напряжения. Под идеальным генератором напряжения будем понимать такой источник, который обеспечивает на любой нагрузке заданное напряжение, внутреннее сопротивление у такого генератора равно нулю. Под идеальным генератором тока будем понимать такой источник, который обеспечивает в любой нагрузке заданный ток, внутреннее сопротивление у такого генератора равно бесконечности. Идеальных генераторов тока и напряжения в природе не существует, поскольку и генераторы тока и генераторы напряжения имеют свое внутреннее сопротивление, которое и ограничивает их возможности.
Если к тому или другому элементу цепи подключить генератор тока или напряжения, то ответной реакцией такого элемента является противодействие изменению своего начального состояния и это противодействие всегда равно приложенному действию, что соответствует третьему закону Ньютона.
Если емкость ![]() заряжена до разности потенциалов
заряжена до разности потенциалов ![]() , то заряд
, то заряд ![]() , накопленный в емкости, определяется соотношением:
, накопленный в емкости, определяется соотношением:
(2.1.1)
Заряд ![]() , зависящий от величины ёмкости и от разности потенциалов на ней, будем называть потоком ёмкостной самоиндукции.
, зависящий от величины ёмкости и от разности потенциалов на ней, будем называть потоком ёмкостной самоиндукции.
Когда речь идет об изменении заряда, определяемого соотношением (2.1.1), то эта величина может изменяться путем изменения разности потенциалов при постоянной емкости, или изменением самой емкости при постоянной разности потенциалов, или и того и другого параметра одновременно. Если величина емкости или разности потенциалов на ней зависят от времени, то величина тока определяется соотношением:
Это выражение определяет закон ёмкостной самоиндукции. Таким образом, ток в цепи, содержащей ёмкость, можно получить двумя способами: изменяя напряжение на ней при постоянной ёмкости или изменяя саму ёмкость при неизменном напряжении на ней, или производить изменение обоих параметров одновременно.
Для случая, когда емкость ![]() постоянна, получаем известное выражение для тока, текущего через емкость:
постоянна, получаем известное выражение для тока, текущего через емкость:
(2.1.2)
В том случае, если изменяется емкость, и на ней поддерживается неизменное напряжение ![]() , имеем:
, имеем:
(2.1.3)
Этот случай относиться к параметрической ёмкостной самоиндукции поскольку наличие тока связано с изменением такого параметра как ёмкость.
Рассмотрим следствия, вытекающие из соотношения (2.1.2).
Если к емкости подключить генератор постоянного тока ![]() , то напряжение на ней будет изменяться по закону:
, то напряжение на ней будет изменяться по закону:
(2.1.4)
Таким образом, емкость, подключенная к источнику постоянного тока, представляет для него активное сопротивление
(2.1.5)
линейно зависящее от времени. Следует отметить, что полученный результат является вполне очевидным, однако такие свойства ёмкости, которую принято считать реактивным элементом, впервые были отмечены в работе [1].
С физической точки зрения это понятно, т.к., чтобы заряжать емкость, источник должен расходовать энергию.
Мощность, отдаваемая источником тока, определяется в данном случае соотношением:
(2.1.6)
Энергию, накопленную емкостью за время ![]() , получим, проинтегрировав соотношение (2.1.6) по времени:
, получим, проинтегрировав соотношение (2.1.6) по времени:
Подставляя сюда значение тока из соотношения (11.4), получаем зависимость величины накопленной в емкости энергии от текущего значения напряжения на ней:
Используя для рассмотренного случая понятие потока электрической индукции, которой является заряд, получаем
(2.1.7)
и используя соотношение (2.1.2), запишем:
(2.1.8)
т.е., если к постоянной емкости подключить источник постоянного тока, то величина тока будет равна производной потока ёмкостной индукции по времени или что то же производной заряда по времени.
Теперь будем поддерживать на емкости постоянное напряжение ![]() , а изменять саму ёмкость, тогда
, а изменять саму ёмкость, тогда
(2.1.9)
Видно, что величина
(2.1.10)
играет роль активного сопротивления. Этот результат тоже физически понятен, т.к. при увеличении емкости увеличивается накопленная в ней энергия, и таким образом, ёмкость отбирает у источника напряжения энергию, представляя для него активную нагрузку. Мощность, расходуемая при этом источником, определяется соотношением:
(2.1.11)
Из соотношения (2.1.11) видно, что в зависимости от знака производной расходуемая мощность может иметь разные знаки. Когда производная положительная, расходуемая мощность идёт на совершение внешней работы. Если производная отрицательная, то работу совершает внешний источник.
Опять, вводя понятие поток ёмкостной индукции
получаем
(2.1.12)
Соотношения (2.1.8) и (2.1.12) указывают на то, что независимо от того, каким способом изменяется поток, его производная по времени всегда равна току.
Рассмотрим еще один процесс, который ранее к законам индукции не относили, однако, он подпадает под наше расширенное определение этого понятия. Из соотношения (2.1.7) видно, что если поток, т.е. заряд, оставить неизменным (будем называть этот режим режимом замороженного ёмкостного потока), то напряжение на емкости можно изменять путем ее изменения. В этом случае будет выполняться соотношение:
где ![]() и
и ![]() - текущие значения, а
- текущие значения, а ![]() и
и ![]() - начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
- начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
Напряжение на емкости и энергия, накопленная в ней, будут при этом определяться соотношениями:
(2.1.13)
Естественно, что данный процесс самоиндукции может быть связан только с изменением самой емкости, и поэтому он подпадает под определение параметрической самоиндукции.
Таким образом, имеются три соотношения (2.1.8), (2.1.12) и (2.1.13), которые определяют процессы ёмкостной самоиндукции. Будем называть их правилами ёмкостного потока. Соотношение (2.1.8) определяет ёмкостную самоиндукцию, при которой отсутствуют изменения емкости, и поэтому эта самоиндукция может быть названа просто ёмкостной самоиндукцией. Соотношения (2.1.3) и (2.1.9–2.1.11) предполагают наличие изменения емкости, поэтому процессы, соответствующие этими соотношениями, будем называть ёмкостной параметрической самоиндукцией.
Перейдем теперь к рассмотрению процессов, происходящих в индуктивности. Введем понятие потока индуктивной самоиндукции
Если индуктивность закорочена, и выполнена из материала, не имеющего активного сопротивления, например из сверхпроводника, то
где ![]() и
и ![]() - какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
- какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
Этот режим будем называть режимом замороженного потока. При этом выполняется соотношение:
(2.1.14)
где ![]() и
и ![]() - текущие значения соответствующих параметров.
- текущие значения соответствующих параметров.
В рассмотренном режиме поток индукции остается неизменным, однако, в связи с тем, что ток в индуктивности может изменяться при ее изменении, такой процесс подпадает под определение параметрической самоиндукции. Энергия, накопленная в индуктивности, при этом будет определяться соотношением
Напряжение на индуктивности, равно производной потока индуктивной индукции по времени:
Рассмотрим случай, когда индуктивность ![]() постоянна, тогда
постоянна, тогда
(2.1.15)
Проинтегрировав выражение (2.1.15) по времени, получим:
(2.1.16)
Таким образом, индуктивность, подключенная к источнику постоянного напряжения, представляет для него активное сопротивление
(2.1.17)
которое уменьшается обратно пропорционально времени.
Мощность, расходуемая при этом источником, определится соотношением:
(2.1.18)
Эта мощность линейно зависит от времени. Проинтегрировав соотношение (2.1.18) по времени, получим энергию, накопленную в индуктивности
(2.1.19)
Подставив в выражение (2.1.19) значение напряжения из соотношения (2.1.16), получаем:
Эта энергия может быть возвращена из индуктивности во внешнюю цепь, если индуктивность отключить от источника питания и подключить к ней активное сопротивление.
Теперь рассмотрим случай, когда ток ![]() , протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
, протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
(2.1.20)
Таким образом, величина
(2.1.21)
играет роль активного сопротивления.
Как и в случае электрического потока, активное сопротивление может быть (в зависимости от знака производной), как положительным, так и отрицательным. Это означает, что индуктивность может, как получать энергию извне, так и отдавать её во внешние цепи.
Вводя обозначение ![]() и, учитывая (2.1.20), получаем:
и, учитывая (2.1.20), получаем:
(2.1.22)
Соотношения (2.1.14), (2.1.19) и (2.1.22) будем называть правилами индуктивной самоиндукции, или правилами потока индуктивной самоиндукции. Из соотношений (2.1.19) и (2.1.22) видно, что, как и в случае с ёмкостным потоком, способ изменения индуктивного потока не влияет на конечный результат, и его производная по времени всегда равна приложенной разности потенциалов. Соотношение (2.1.19) определяет индуктивную самоиндукцию, при которой отсутствуют изменения индуктивности, и поэтому она может быть названа просто индуктивной самоиндукцией. Соотношения (2.1.20–2.1.21) предполагают наличие изменений индуктивности, поэтому процессы, описываемые этими соотношениями, будем называть индуктивной параметрической самоиндукцией.
Новый способ получения волнового уравнения для длинных линий
Процессы, рассмотренные в предыдущем разделе, касаются цепей с сосредоточенными параметрами, когда распределение разностей потенциалов и токов в рассмотренных элементах можно считать однородным. Однако имеются цепи, например длинные линии, в которых разности потенциалов и токи не являются пространственно однородными. Эти процессы описываются волновыми уравнениями, которые могут быть получены из уравнений Максвелла или при помощи телеграфных уравнений, но физика самого явления нам не ясна.
Воспользуемся результатами, полученными в предыдущем разделе для рассмотрения процессов, происходящих в длинных линиях, в которых емкость и индуктивность являются распределенными параметрами. Предположим, что погонная (приходящаяся на единицу длины) емкость и индуктивность такой линии составляют соответственно ![]() и
и ![]() . Если к такой линии подключить источник постоянного напряжения
. Если к такой линии подключить источник постоянного напряжения ![]() , то его фронт будет распространяться в линии с какой-то скоростью
, то его фронт будет распространяться в линии с какой-то скоростью ![]() , и текущая координата этого фронта определится соотношением
, и текущая координата этого фронта определится соотношением ![]() . При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
. При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
Источник напряжения ![]() будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением (2.1.9) должен течь ток:
будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением (2.1.9) должен течь ток:
(2.2.1)
Этот ток будет протекать через проводники линии, обладающие индуктивностью. Но, поскольку индуктивность линии в связи с движением фронта напряжения, тоже увеличивается, то в соответствии с соотношением (2.1.20), на ней будет наблюдаться падение напряжения:
Но падение напряжения на проводниках линии по абсолютной величине равно напряжению, приложенному к её входу, поэтому в последнем выражении следует допустить, что ![]() . С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения
. С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения ![]() должна составлять
должна составлять
(2.2.2)
Это выражение соответствует скорости распространения электромагнитных колебаний в самой линии. Следовательно, если к бесконечно длинной линии подключить источник напряжения, то в ней будет иметь место саморасширение и ёмкостного и индуктивного потоков, заполняющих линию энергией, и скорость фронта постоянного напряжения и тока будет равна скорости распространения электромагнитных колебаний в такой линии. Такую волну будем называть электротоковой. Интересно отметить, что полученный результат не зависит от вида функции ![]() , т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (2.2.2) . Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью
, т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (2.2.2) . Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью ![]() , оставляет за собой линию, заряженную до разности потенциалов
, оставляет за собой линию, заряженную до разности потенциалов ![]() , что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток
, что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток ![]() , что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
, что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
Величину тока в линии можно получить, подставив значения скорости распространения фронта волны, определяемого соотношением (2.2.2), в соотношение (2.2.1). Сделав эту подстановку, получим
где  - волновое сопротивление линии.
- волновое сопротивление линии.
В данном случае
Так точно
Видно, что правила потока и для индуктивной и для ёмкостной самоиндукции соблюдаются и в этом случае.
Таким образом, процессы распространения разности потенциалов вдоль проводников длинной линии и постоянного тока в ней являются связанными и взаимно дополняющими друг друга, и существовать друг без друга не могут. Такой процесс можно называть ёмкостно-ндуктивной самопроизвольной параметрической самоиндукцией. Такое название связано с тем, что расширение потоков происходят самопроизвольно и характеризуют скорость процесса заполнения линии энергией. Из выше изложенного становится понятной связь между энергетическими процессами и скоростью распространения фронтов волны в длинных линиях. Поскольку при излучении электромагнитных волн свободное пространство тоже является передающей линией, то подобные законы должны характеризовать и распространение в таком пространстве.
Что будет, например, в том случае, если в качестве одного из проводников длинной линии взять спираль, или как это принято называть, длинный соленоид. Очевидно, в этом случае скорость распространения фронта напряжения в такой линии уменьшится, поскольку погонная индуктивность линии увеличится. При этом такому распространению будет сопутствовать процесс распространения не только внешних, по отношению к соленоиду полей и токов, но и процесс распространения магнитного потока внутри самого соленоида и скорость распространения такого потока будет равна скорости распространения электромагнитной волны в самой линии. Зная ток и напряжение в линии, можно вычислить удельную энергию, заключенную в погонной ёмкости и индуктивности линии. Эти энергии будут определяться соотношениями:
(2.2.3)
(2.2.4)
Теперь обсудим вопрос о длительности фронта электротоковой волны и о том, какое пространство этот фронт будет занимать в самой линии. Ответ на первый вопрос определяется свойствами самого источника напряжения, т.к. локальная производная ![]() на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время
на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время ![]() , то в линии он займет участок длиной
, то в линии он займет участок длиной ![]() . Если к линии приложить напряжение, меняющееся со временем по закону
. Если к линии приложить напряжение, меняющееся со временем по закону ![]() , то это же значение функции будет наблюдаться в любой точке линии на расстоянии
, то это же значение функции будет наблюдаться в любой точке линии на расстоянии ![]() от ее начала с запаздыванием
от ее начала с запаздыванием ![]() . Таким образом, функция
. Таким образом, функция
(2.2.5)
может быть названа функцией распространения, т.к. она устанавливает связь между локальными временными и пространственными значениями функции в линии. Длинная линия является устройством, которое локальные производные напряжения по времени на входе линии превращает в пространственные производные в самой линии. На основании функции распространения (2.2.5) можно установить связь между локальными и пространственными производными в длинной линии. Очевидно, что
Важно отметить, что сам процесс распространения в данном случае обязан естественному саморасширению электрического поля и тока в линии, и он подчиняется правилам параметрической самоиндукции. Во-вторых, для решения волновых уравнений длинных линий
(2.2.6)
полученных из телеграфных уравнений
требуется знание вторых производных напряжений и токов.
Но как быть, если на вход линии подаётся напряжение, у которого вторая производная равна нулю (случай, когда напряжение источника меняется по линейному закону)? Ответа на этот вопрос уравнения (2.2.6) не дают.
Используемый метод даёт ответ на такой вопрос.
При рассмотрении процессов в длинной линии фигурировали такие понятия как погонная емкость и индуктивность, а также токи и напряжения в линии. Однако в электродинамике, основанной на уравнениях Максвелла, нет таких понятий как емкость и индуктивность, а есть понятия электрической и магнитной проницаемости среды. В проведенном рассмотрении также отсутствовали такие понятия как электрические и магнитные поля. Покажем, как перейти от таких категорий как «погонная индуктивность и ёмкость», и «ток» и «напряжение» в линии к таким понятиям как «диэлектрическая и магнитная проницаемость», а также «электрическое и магнитное поле». Для этого возьмем простейшую конструкцию линии, расположенную в вакууме, как показано на рис. 5.
Рис. 5. Двухпроводная линия, состоящая из двух идеально проводящих плоскостей
Будем считать, что ![]() >>
>> ![]() и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
(2.2.7)
(2.2.8)
где ![]() и
и ![]() - магнитная и диэлектрическая проницаемость вакуума.
- магнитная и диэлектрическая проницаемость вакуума.
Фазовая скорость в такой линии будет определяться соотношением:
где ![]() - скорость распространения света в вакууме.
- скорость распространения света в вакууме.
Волновое сопротивление рассмотренной линии будет равно:
где  - волновое сопротивление свободного пространства.
- волновое сопротивление свободного пространства.
Кроме этого при соблюдении условия ![]() получаем равенство
получаем равенство ![]() . Это означает, что магнитная проницаемость играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство
. Это означает, что магнитная проницаемость играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство ![]() . Это означает, что диэлектрическая проницаемость
. Это означает, что диэлектрическая проницаемость ![]() играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и
играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и ![]() , и
, и ![]() приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
Рассмотрение электромагнитной волны в длинной линии можно рассматривать как заполнение пространства, находящегося между её проводниками, особым видом материи, которую представляют электрические и магнитные поля. Математически можно считать, что эти поля сами обладают удельной энергией и при их помощи можно передавать энергию по линиям передач. Если же рассматривать процессы, протекающие при излучении электромагнитных волн при помощи какой-либо антенны, то его можно рассматривать также как заполнение свободного пространства этим видом материи. Однако геометрический вид полей и токов в этом случае будет сложнее, поскольку всегда будут присутствовать как поперечные, так и продольные составляющие полей. Такой подход исключает необходимость применения, для описания распространения электромагнитных волн, такой субстанции как эфир.
Если к рассмотренной линии бесконечной длины, или линии нагруженной волновым сопротивлением, подключить источник постоянного напряжения ![]() , то напряженность поля в линии составит:
, то напряженность поля в линии составит:
а ток, текущий в линию от источника питания, будет определяться соотношением:
(2.2.9)
Магнитное поле в линии будет равно удельному току, протекающему в линии
Подставляя сюда значение ![]() , получаем
, получаем
(2.2.10)
Такая же связь между электрическим и магнитным полем существует и для случая поперечных электромагнитных волн, распространяющихся в свободном пространстве.
Сравнивая выражения для энергий, нетрудно видеть, что удельные энергии могут быть выражены через электрические и магнитные поля
(2.2.11)
Это означает, что удельная энергия, накопленная в магнитном и электрическом поле в такой линии одинакова. Если значения этих энергий умножить на объемы, занимаемые полями, то полученные величины совпадают с выражениями (2.2.3–2.2.4).
Таким образом, приходим к выводу, что в рассмотренной линии распространяются такие же поперечные плоские волны, как и в свободном пространстве. Причем этот вывод получен не путём решения уравнений Максвелла, а путём рассмотрения динамических процессов, которые отнесены к разряду параметрической самоиндукции. Особенностью такой линии будет то, что в ней, в отличие от свободного пространства, могут распространяться постоянные магнитные и электрические поля, а этот случай не может быть рассмотрен путем решения уравнений Максвелла.
Следовательно, условно можно считать, что длинная линия является устройством, которое при подключении к ней источника постоянного напряжения заполняется двумя видами энергии: электрической и магнитной. Удельные плотности этих энергий равны, а поскольку и электрическая и магнитная энергии заполняют одинаковые объемы, то и общая энергия, накопленная в этих полях одинакова. Особенностью данной линии является то, что при протекании в линии постоянного тока распределение электрического и магнитного полей в ней является однородным. Нетрудно показать, что сила, действующая на проводники такой линии, равна нулю. Это следует из соотношения (2.2.11), в котором его правая и левая части представляют удельные силы, приложенные к плоскостям линии. Но электрическая и магнитная силы имеют разные знаки, поэтому они компенсируют друг друга. Этот вывод касается и передающих линий любой другой конфигурации.
Если к линии приложить напряжение, меняющееся со временем по любому закону![]() , то по аналогии с (2.2.5) можно записать
, то по аналогии с (2.2.5) можно записать
(2.2.12)
Аналогичное соотношение будет и для магнитных полей.
Очевидно, что произведение ![]() представляет мощность
представляет мощность ![]() , передаваемую через поперечное сечение линии в направлении
, передаваемую через поперечное сечение линии в направлении ![]() . Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим
. Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим ![]() . Произведение
. Произведение ![]() представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
Таким образом, все выводы, полученные на основании рассмотрения процессов в длинной линии двумя методами, совпадают. Поэтому и в дальнейшем, не рискуя допустить ошибки принципиального характера, можно для описания процессов в длинных линиях с успехом пользоваться такими параметрами, как распределенная индуктивность и ёмкость. Конечно, при этом следует понимать, что ![]() и
и ![]() это некоторые интегральные характеристики, не учитывающие структуру полей. Следует отметить, что с практической точки зрения, применение параметров
это некоторые интегральные характеристики, не учитывающие структуру полей. Следует отметить, что с практической точки зрения, применение параметров ![]() и
и ![]() имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.
имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.
Новые подходы к вопросам излучения и распространения электромагнитных волн
Динамические потенциалы и поля движущихся зарядов
При распространении волны в длинной линии она, как показано в предыдущем разделе, заполняется двумя видами энергии, которые могут быть определены через токи и напряжения или через электрические и магнитные поля в линии. И только после того, как волна заполнит электромагнитной энергией всё пространство между генератором напряжения и нагрузкой на нагрузке начнёт выделяться энергия. Т.е. то время, на которое задерживается этот процесс, генератор расходовал свою мощность на заполнение энергией участка линии между генератором и нагрузкой. Но если начать нагрузку удалять от входа линии, то количество выделяемой на ней энергии уменьшится, т.к. часть энергии, расходуемой источником, уйдёт на заполнение энергией дополнительной длины линии, связанной с движением нагрузки. Если нагрузка будет приближаться к источнику, то она будет получать дополнительное количество энергии за счёт сокращения её длины. Но если нагрузкой линии является активное сопротивление, то увеличение или уменьшение расходуемой в нём мощности может быть связано только с изменением напряжения на таком сопротивлении. Поэтому приходим к выводу, что при движении наблюдателя относительно уже существующих в линии полей должно приводить к их изменению.
Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами, а также электромагнитными волнами, которые генерируются неподвижными и движущимися источниками таких волн. Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
В классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся не выясненной.
В данном разделе будет сделана попытка найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [1-4], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы, как показано в предыдущей главе записываются следующим образом:
(3.1.1)
или
(3.1.2)
Для постоянных полей эти соотношения имеют вид:
(3.1.3)
В соотношениях (3.1.1-3.1.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (3.1.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (3.1.1–3.1.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (3.1.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [5]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [5]. Электрическое поле  за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [1-4]:
(3.1.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
При движении в магнитном поле, применяя уже рассмотренный метод, получаем:
где ![]() - скорость нормальная к направлению магнитного поля.
- скорость нормальная к направлению магнитного поля.
Если применить полученные результаты к электромагнитной волне и обозначить компоненты полей параллельные скорости ИСО, как ![]() и
и ![]() , а
, а ![]() и
и ![]() , как компоненты нормальные к ней, то преобразования полей запишутся:
, как компоненты нормальные к ней, то преобразования полей запишутся:
(3.1.5)
где  – импеданс свободного пространства,
– импеданс свободного пространства,  – скорость света.
– скорость света.
Преобразования полей (3.1.5) были впервые получены в работе [5].
Фазовая аберрация и поперечный эффект Доплера
В этом параграфе будет показано, как при помощи соотношений (3.1.5) можно объяснить явление фазовой аберрации, которое в рамках существующей классической электродинамики объяснений не имело. Будем считать, что имеются компоненты плоской волны ![]() и
и ![]() , распространяющейся в направлении
, распространяющейся в направлении ![]() , а штрихованная система движется в направлении оси
, а штрихованная система движется в направлении оси ![]() со скоростью
со скоростью ![]() . Тогда компоненты полей в штрихованной системе координат в соответствии с соотношениями (3.1.5) запишутся:
. Тогда компоненты полей в штрихованной системе координат в соответствии с соотношениями (3.1.5) запишутся:
Таким образом, имеется неоднородная волна, имеющая в направлении распространения компоненту ![]() .
.
Запишем суммарное поле ![]() в движущейся ИСО:
в движущейся ИСО:
(3.2.1)
Если вектор ![]() по-прежнему ортогонален оси
по-прежнему ортогонален оси ![]() , то вектор
, то вектор ![]() теперь наклонен к ней на угол
теперь наклонен к ней на угол ![]() , определяемый соотношением:
, определяемый соотношением:
(3.2.2)
Это и есть фазовая аберрация. Именно на такой угол приходиться наклонять телескоп по ходу движения Земли вокруг Солнца, чтобы наблюдать звезды, находящиеся в действительности в зените.
Вектор Пойнтингa теперь также направлен уже не по оси ![]() , а находясь в плоскости
, а находясь в плоскости ![]() , наклонен к оси
, наклонен к оси ![]() на угол, определяемый соотношениями (3.2.2). Отношение же абсолютных величин векторов
на угол, определяемый соотношениями (3.2.2). Отношение же абсолютных величин векторов ![]() и
и ![]() в обеих системах остались одинаковыми. Однако абсолютная величина самого вектора Пойнтинга увеличилась. Таким образом, даже поперечное движение инерциальной системы по отношению к направлению распространения волны увеличивает ее энергию в движущейся системе. С физической точки зрения это явление понятно. Можно привести пример с дождевыми каплями. Когда они падают вертикально, то энергия у них одна. Но в инерциальной системе, двигающейся нормально к вектору их скорости, к этой скорости добавляется вектор скорости инерциальной системы. При этом абсолютная величина скорости капель в инерциальной системе будет равна корню квадратному из суммы квадратов указанных скоростей. Такой же результат дает нам и соотношение (3.2.1).
в обеих системах остались одинаковыми. Однако абсолютная величина самого вектора Пойнтинга увеличилась. Таким образом, даже поперечное движение инерциальной системы по отношению к направлению распространения волны увеличивает ее энергию в движущейся системе. С физической точки зрения это явление понятно. Можно привести пример с дождевыми каплями. Когда они падают вертикально, то энергия у них одна. Но в инерциальной системе, двигающейся нормально к вектору их скорости, к этой скорости добавляется вектор скорости инерциальной системы. При этом абсолютная величина скорости капель в инерциальной системе будет равна корню квадратному из суммы квадратов указанных скоростей. Такой же результат дает нам и соотношение (3.2.1).
Нетрудно показать, что, если поляризация электромагнитной волны измениться, то результат останется прежним. Преобразования по отношению к векторам ![]() и
и ![]() полностью симметричны, единственным отличием будет то, что теперь получиться волна, у которой появиться в направлении распространения компонента
полностью симметричны, единственным отличием будет то, что теперь получиться волна, у которой появиться в направлении распространения компонента ![]() .
.
Полученные волны имеют в направлении своего распространения дополнительные вектора электрического или магнитного поля, и в этом они похожи на ![]() и
и ![]() волны, распространяющиеся в волноводах. В данном случае возникает необычная волна, у которой фазовый фронт наклонен к вектору Пойнтинга на угол, определяемый соотношением (3.2.2). По сути дела полученная волна является суперпозицией плоской волны с фазовой скоростью
волны, распространяющиеся в волноводах. В данном случае возникает необычная волна, у которой фазовый фронт наклонен к вектору Пойнтинга на угол, определяемый соотношением (3.2.2). По сути дела полученная волна является суперпозицией плоской волны с фазовой скоростью 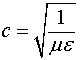 и дополнительной волны ортогональной к направлению распространения плоской волны и имеющей бесконечную фазовую скорость.
и дополнительной волны ортогональной к направлению распространения плоской волны и имеющей бесконечную фазовую скорость.
Рассмотрим еще один случай, когда направление скорости движущейся системы совпадает с направлением распространения электромагнитной волны. Будем считать, что имеются компоненты плоской волны ![]() и
и ![]() , а также компоненты скорости
, а также компоненты скорости ![]() . Учитывая, что в этом случае выполняется соотношение
. Учитывая, что в этом случае выполняется соотношение ![]() , получаем:
, получаем:
Т.е. амплитуды полей экспоненциально убывают или возрастают в зависимости от направления движения.
Волновому уравнению удовлетворяет волна напряжённости электрического (или магнитного) поля типа:
При переходе в инерциальную систему, движущуюся со скоростью ![]() наблюдается доплеровский сдвиг частоты.
наблюдается доплеровский сдвиг частоты.
Поперечный эффект Доплера, который обсуждается достаточно давно, до сих пор не нашел своего уверенного экспериментального подтверждения. Для наблюдения звезды из движущейся ИСО необходимо наклонять телескоп по ходу движения на угол, определяемый соотношением (3.2.2). Но в данном случае та звезда, наблюдаемая при помощи телескопа в зените, будет в действительности находиться несколько позади видимого положения по отношению к направлению движения. Ее угловое смещение от видимого положения при этом будет определяться тоже соотношением (3.2.2). Но это будет означать, что такая звезда по отношению к нам имеет радиальную составляющую скорости, определяемую соотношением
![]()
Поскольку для малых значений углов ![]() , а
, а 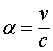 , то доплеровский сдвиг частоты составит
, то доплеровский сдвиг частоты составит
(3.2.3)
Данный результат численно совпадает с результатами СТО, но он принципиально отличается от её результатов тем, что в СТО считается, что поперечный эффект Доплера, определяемый соотношением (3.2.3), существует на самом деле, в то время как в данном случае это только кажущийся эффект. Если сравнить результаты преобразований полей (3.1.5) с преобразованиями СТО, то нетрудно увидеть, что они совпадают с точностью до квадратичных членов отношения скорости движения заряда к скорости света.
Преобразования СТО, хотя и были основаны на постулатах, но смогли правильно объяснить достаточно точно многие физические явления, которые до этого объяснения не имели. С этим обстоятельством и связан такой большой успех данной теории. Преобразования (3.1.4) и (3.1.5) получены на физической основе без использования постулатов и оказалось, что они с высокой точностью совпали с СТО. Отличием является то, что в преобразованиях (3.1.5) нет ограничений по скорости для материальных частиц, а также то, что заряд не является инвариантом скорости. Экспериментальное подтверждение указанного факта и может послужить подтверждением правильности предлагаемых преобразований.
Законы электро-электрической индукции
Поскольку любой процесс распространения электрических полей и потенциалов всегда связан с запаздыванием, введём запаздывающий скалярно-векторный потенциал, считая, что поле этого потенциала распространяется в данной среде со скоростью света:
(3.3.1)
где  – составляющая скорости заряда
– составляющая скорости заряда ![]() , нормальная к вектору
, нормальная к вектору ![]() в момент времени
в момент времени  ,
, ![]() – расстояния между зарядом и точкой, в которой определяется поле, в момент времени
– расстояния между зарядом и точкой, в которой определяется поле, в момент времени ![]() .
.
Но возникает вопрос, на каких основаниях, если не использовать уравнения Максвелла, из которого следует волновое уравнение, вводится запаздывающий скалярно-векторный потенциал? Этот вопрос рассматривался в тринадцатом параграфе, когда определялась скорость распространения фронта волны напряжённости магнитного и электрического поля в длинной линии. Там, не прибегая к уравнениям Максвелла, было показано, что электрическое и магнитное поле распространяются с конечной скоростью, которая в вакуумной линии равна скорости света. Следовательно, такие поля запаздывают на время ![]() (см. соотношение (13.12)). Такое же запаздывание вводим в данном случае и для скалярно-векторного потенциала, который является носителем электрических полей.
(см. соотношение (13.12)). Такое же запаздывание вводим в данном случае и для скалярно-векторного потенциала, который является носителем электрических полей.
Используя соотношение ![]() , найдём поле в точке 1 (рис. 6) .
, найдём поле в точке 1 (рис. 6) .
Рис. 6. Схема формирования индуцированного электрического поля.
Градиент числового значения радиуса вектора ![]() есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси
есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси ![]() и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая:
и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая:
1) точка истока фиксирована и ![]() рассматривается как функция положения точки наблюдения;
рассматривается как функция положения точки наблюдения;
2) точка наблюдения фиксирована и ![]() рассматривается как функция положения точки истока.
рассматривается как функция положения точки истока.
Будем считать, что заряд ![]() совершает колебательное движение вдоль оси
совершает колебательное движение вдоль оси ![]() , в окрестности точки 0, которая является точкой наблюдения, а точкой истока является фиксированная точка 1 и
, в окрестности точки 0, которая является точкой наблюдения, а точкой истока является фиксированная точка 1 и ![]() рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
При условии, что амплитуда колебаний заряда значительно меньше, чем расстояние до точки наблюдения, можно считать радиус вектор постоянная величина. При этом условии получаем:
(3.3.2)
где ![]() - какая-то фиксированная точка на оси
- какая-то фиксированная точка на оси ![]() .
.
Учитывая, что
из (21.2) получаем:
(3.3.3)
Это и есть полный закон излучения движущегося заряда.
Если взять только первый член разложения 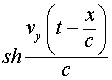 , то из (3.3.3) получим
, то из (3.3.3) получим
(3.3.4)
где  - запаздывающее ускорение заряда.
- запаздывающее ускорение заряда.
Это соотношение является волновым уравнением и определяет как амплитудные, так и фазовые характеристики волны электрического поля, излучаемого движущимся зарядом.
Если в качестве направления излучения взять вектор, лежащий в плоскости ![]() , и составляющий с осью
, и составляющий с осью ![]() угол
угол ![]() , то соотношение (21.4) принимает вид:
, то соотношение (21.4) принимает вид:
(3.3.5)
Соотношение (3.3.5) определяет диаграмму направленности излучения. Поскольку в данном случае есть осевая симметрия относительно оси ![]() , то можно вычислить полную диаграмму направленности рассмотренного излучателя. Эта диаграмма соответствует диаграмме направленности дипольного излучателя.
, то можно вычислить полную диаграмму направленности рассмотренного излучателя. Эта диаграмма соответствует диаграмме направленности дипольного излучателя.
Поскольку  - запаздывающий векторный потенциал, то соотношение (3.3.5) можно переписать
- запаздывающий векторный потенциал, то соотношение (3.3.5) можно переписать
Опять получено полное совпадение с уравнениями запаздывающего векторного потенциала в классической электродинамики, но векторный потенциал введён здесь не эвристическим феноменологическим способом, а с использованием понятия запаздывающего скалярно-векторного потенциала. Нужно отметить одно важное обстоятельство: в уравнениях Максвелла электрические поля, представляющие волну, вихревые. В данном же случае электрические поля носят градиентный характер.
Продемонстрируем ещё одну возможность, которую открывает соотношение (3.3.5). Известно, что в электродинамике существует такое понятие, как электрический диполь и дипольное излучение, когда заряды, колеблющиеся в электрическом диполе, излучают электромагнитные волны. Два заряда с противоположными знаками имеют дипольный момент:
(3.3.6)
где вектор ![]() направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
Следовательно
и
Подставляя данное соотношение в выражение (3.3.5), получаем закон излучения колеблющегося диполя.
(3.3.7)
Это также очень хорошо известное соотношение [6].
Таким образом, в процессе колебания электрического диполя создаются электрические поля двух видов. Во-первых, это электрические индукционные поля излучения, представляемые соотношениями (3.3.4), (3.3.5) и (3.3.6), связанные с ускорением заряда. С другой стороны, вокруг колеблющегося диполя образуются электрические поля статического диполя, которые изменяются во времени в связи с тем, что расстояние между зарядами зависит от времени. Суммарное же значение поля, вокруг такого диполя определяют как суперпозицию полученных полей.
Законы (3.3.4), (3.3.5), (3.3.7) - это законы прямого действия, в которых уже нет ни магнитных полей, ни векторных потенциалов. Т.е. те строительные леса, которыми являлись магнитное поле и магнитный векторный потенциал уже сняты и они нам больше не нужны.
Используя соотношение (3.3.5) можно получить законы отражения и рассеивания как для одиночных зарядов, так и, для любого их количества. Если какой-либо заряд или группа зарядов подвергаются действию внешнего (стороннего) электрического поля, то такие заряды начинают осуществлять вынужденное движение, и каждый из них излучает электрические поля в соответствии с соотношением (3.3.5). Суперпозиция электрических полей, излучаемых всеми зарядами, является электрической волной.
Если на заряд действует стороннее электрическое поле ![]() , то ускорение заряда определяют как:
, то ускорение заряда определяют как:
С учётом этого соотношение (3.3.11) принимает вид
(3.3.8)
где коэффициент  может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
Волне электрического поля (3.3.5) сопутствует волна тока смещения:
Если заряд осуществляет своё движение под воздействием стороннего электрического поля ![]() , то ток смещения в дальней зоне записывают:
, то ток смещения в дальней зоне записывают:
(3.3.9)
Суммарная волна, которая представляет распространение электрических полей (3.3.8) и токов смещения (3.3.9), может быть названа электротоковой. В этой волне ток смещения отстаёт от волны электрического поля на ![]() .
.
Впервые этот термин и определение такой волны было дано в работах [2, 3]. Параллельно с электрическими волнами можно ввести магнитные волны, если положить, что
(3.3.10)
Введённое таким образом магнитное поле является вихревым. Сравнивая (3.3.9) и (3.3.10) получаем:
Интегрируя это соотношение по координате, находим значение магнитного поля
(3.3.11)
Таким образом, соотношения (3.3.8), (3.3.9) и (3.3.11) могут быть названы законами электро-электрической индукции, т.к. дают непосредственную связь между прикладываемыми к заряду сторонними электрическими полями и полями индуцируемыми этим зарядом в его окрестности. Сам же заряд выступает в данном случае в роли своеобразного трансформатора, обеспечивающего такое переизлучение.
Магнитное поле, которое можно вычислить при помощи соотношения (3.3.11), направлено нормально и к электрическому полю и к направлению распространения, а их отношение в каждой точке пространства составляет:
где ![]() - волновое сопротивление свободного пространства.
- волновое сопротивление свободного пространства.
Волновое сопротивление определяет активную мощность потерь на единичной площадке, расположенной нормально к направлению распространения волны:
Поэтому электротоковая волна, пересекая такую площадку, переносит через неё мощность, определяемую данным соотношением, что находится в согласии с теоремой Пойнтинга о потоке мощности электромагнитной волны. Поэтому, для нахождения всех параметров, характеризующих волновой процесс, распространения и переноса энергии посредством полей, достаточно рассмотрения лишь электротоковой волны и знания волнового сопротивления пространства. При этом совсем не обязательно вводить такое понятие, как «магнитное поле» и его векторный потенциал, хотя ничего незаконного в этом нет. В такой постановке соотношения, полученные для электрического и магнитного поля, полностью удовлетворяют теореме Гельмгольца. Эта теорема гласит, что всякое однозначное и непрерывное векторное поле ![]() , обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции
, обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции ![]() и ротора некоторой векторной функции
и ротора некоторой векторной функции ![]() , дивергенция которой равна нулю:
, дивергенция которой равна нулю:
Следовательно, должно существовать чёткое разделение полей на градиентные и вихревые. Видно, что в полученных выражениях для индуцируемых полей такое разделение имеется. Электрические поля носят градиентный характер, а магнитные – вихревой.
Таким образом, построение электродинамики нужно было начинать с признания зависимости скалярного потенциала от скорости, как это предлагал Вебер. Но в том-то и дело, что природа очень глубоко прячет свои секреты, и, чтобы прийти к такому простому выводу, пришлось пройти путь длиной почти в два столетия. Металлические опилки, которые так дружно выстраивались вокруг полюсов магнита, прямым образом указывали на наличие каких-то силовых полей потенциального характера, но на это не обратили внимания, поэтому и оказалось, что все разглядели только верхушку айсберга, значительная часть которого оставалась невидимой почти двести лет.
С учётом всего сказанного следует полагать, что в основе подавляющего большинства статических и динамических явлений в электродинамике лежит одна единственная формула (3.3.1), предполагающая зависимость скалярного потенциала заряда от скорости его движения. Из неё следует и статическое взаимодействие зарядов, и законы силового взаимодействия в случае их взаимного движения, и законы излучения и рассеивания. Такой подход позволил объяснить с позиций классической электродинамики следующие явления: фазовая аберрация и поперечный эффект Доплера, которые в рамках существующей классической электродинамики объяснения не находили.
После всего сказанного можно снять строительные леса, такие как магнитное поле и магнитный векторный потенциал, которые не позволяют вот уже почти двести лет увидеть здание электродинамики во всём его величии и красоте.
Список литературы
- 1. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 2. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с.
- 3. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 4. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 5. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 6. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.