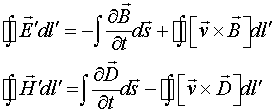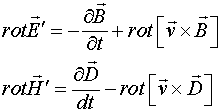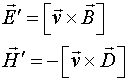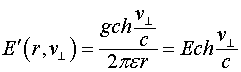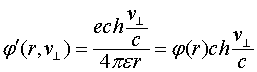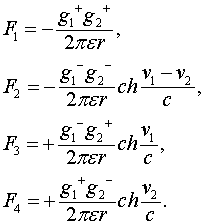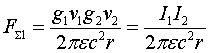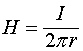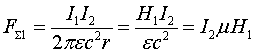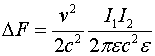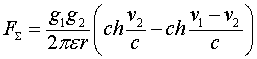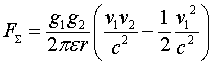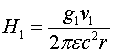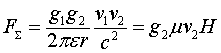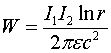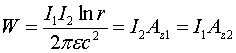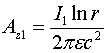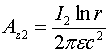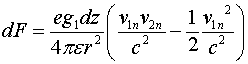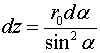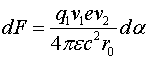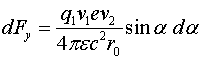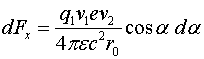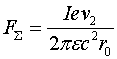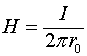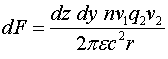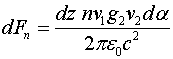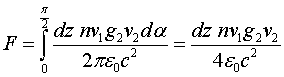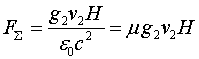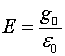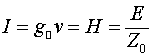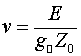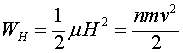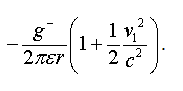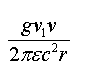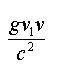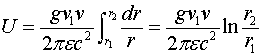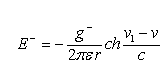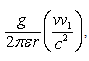Ещё раз об униполярной индукции
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
Униполярная индукция была открыта ещё Фарадеем почти 200 лет тому назад, но в классической электродинамике окончательного ответа на то, как и почему работает униполярный генератор, нет до настоящего времени [1]. Особо непонятен случай, когда имеется вращающийся намагниченный проводящий цилиндр, при движении которого между неподвижными контактами, подключёнными к его оси и образующей, возникает э.д.с. Ещё более непонятен случай, когда вместе с цилиндрическим магнитом вращается проводящий диск, а неподвижные контакты подключены к оси диска и его образующей. В некоторых источниках говорится, что ответ может быть получен в рамках СТО, но нет конкретных ссылок, как именно СТО объясняет указанные случаи. Ниже будет показано, что конкретные ответы на все эти вопросы могут быть получены в рамках концепции зависимости скалярного потенциала заряда от его относительной скорости. Мы рассмотрим несколько вариантов униполярны генераторов и их работу с точки зрения этой концепции.
Динамические потенциалы и поля движущихся зарядов
Тот путь, который будет продемонстрирован в этой статье, касающийся введения в законах индукции полных производных полей, прошел в значительной части в своё время ещё Герц. Правда, он не вводил понятие векторных потенциалов, а оперировал только полями, но это не умаляет его заслуг. Герц ошибался лишь в том, что считал электрические и магнитные поля инвариантами скорости.
Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами. Поля, которые создаются в данной ИСО движущимися зарядами, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов в процессе их ускорения.
Как уже отмечалось, в классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной [2].
В данном статье будет сделана попытка найти физически обоснованные причин силового взаимодействия токонесущих систем, а также понять принципы работы униполярных генераторов. Первый шаг, продемонстрированный в работах [3-7], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы записываются следующим образом:
(1.1)
или
(1.2)
Для постоянных полей эти соотношения имеют вид:
(1.3)
В соотношениях (1.1-1.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (1.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (1.1), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (1.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [3].
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [3].
Электрическое поле 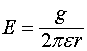 за пределами длинного заряженного стержня, на единицу длины которого приходится заряд
за пределами длинного заряженного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать со скоростью
начать со скоростью ![]() двигать другую ИСО, то в ней появится дополнительное магнитное поле
двигать другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле движущегося одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [3-7]:
(1.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к направлению движения самого заряда.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к направлению движения самого заряда.
Силовое взаимодействие токонесущих систем
Уравнения Максвелла не содержат в себе информации о силовом взаимодействии токонесущих систем. В классической электродинамике для расчета такого взаимодействия нужно рассчитать магнитное поле в заданной области пространства, а затем, используя силу Лоренца, которая вводится как отдельный экспериментальный постулат, находить силы, действующие на заряды, движущиеся в заданном поле. При таком подходе неясным остается вопрос о том, к чему приложены силы реакции по отношению к тем силам, которые действуют на движущиеся заряды.
Концепция магнитного поля возникла в значительной степени благодаря наблюдениям за силовым взаимодействием токонесущих и намагниченных систем. Особенно показательным является опыт с железными опилками, которые выстраиваются около полюсов магнита или вокруг кольцевого витка с током в чёткие геометрические фигуры. Эти фигуры и послужили поводом для введения такого понятия, как силовые линии. При любом силовом взаимодействии, в соответствии с третьим законом Ньютона, всегда существует равенство сил действия и противодействия, а также всегда имеются те элементы системы, к которым эти силы приложены. Большим недостатком концепции магнитного поля является то, что она не даёт ответа на то, куда конкретно приложены силы действия и противодействия, т.к. магнитное поле выступает как самостоятельная субстанция, с которой и происходит взаимодействие движущихся зарядов.
Экспериментально известно, что силы взаимодействия в токонесущих системах приложены к тем проводникам, движущиеся заряды которых создают магнитное поле. Однако в существующей концепции силового взаимодействия токонесущих систем, основанной на понятиях магнитного поля и силы Лоренца, положительно заряженная решетка, которая является остовом проводника и к которой приложены силы, не участвует в формировании сил взаимодействия. То, что положительно заряженные ионы принимают непосредственное участие в силовых процессах, говорит уже, хотя бы, тот факт, что в процессе сжатия плазмы, при протекании через нее постоянного тока происходит сжатие и ионов (так называемый пинч-эффект).
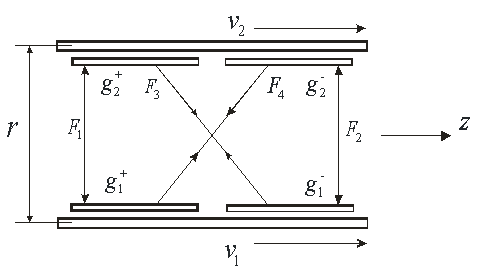
Рассмотрим этот вопрос на основе концепции скалярно-векторного потенциала. Будем считать, что скалярно-векторный потенциал одиночного заряда определяется соотношением (16.4), и что электрические поля, создаваемые этим потенциалом, действуют на все окружающие заряды, в том числе и на заряды положительно заряженной решетки.
Рис. 1. Силового взаимодействия проводов двухпроводной линии.
Разберем с этих позиций силовое взаимодействие между двумя параллельными проводниками (рис. 1), по которым протекают токи. Будем считать, что ![]() ,
, ![]() и
и ![]() ,
, ![]() представляют соответственно неподвижные и движущиеся заряды, приходящиеся на единицу длины проводника.
представляют соответственно неподвижные и движущиеся заряды, приходящиеся на единицу длины проводника.
Заряды ![]() ,
, ![]() представляют положительно заряженную решетку в нижнем и верхнем проводниках. Будем также считать, что оба проводника до начала движения зарядов являются электронейтральными, т.е. в проводниках имеется две системы взаимно вложенных разноименных зарядов с удельной плотностью на
представляют положительно заряженную решетку в нижнем и верхнем проводниках. Будем также считать, что оба проводника до начала движения зарядов являются электронейтральными, т.е. в проводниках имеется две системы взаимно вложенных разноименных зарядов с удельной плотностью на ![]() ,
, ![]() и
и ![]() ,
, ![]() , которые электрически нейтрализуют друг друга. На рис. 1 эти системы для большего удобства рассмотрения сил взаимодействия раздвинуты по оси z. Подсистемы с отрицательным зарядом (электроны) могут двигаться со скоростями
, которые электрически нейтрализуют друг друга. На рис. 1 эти системы для большего удобства рассмотрения сил взаимодействия раздвинуты по оси z. Подсистемы с отрицательным зарядом (электроны) могут двигаться со скоростями ![]() и
и ![]() . Силу взаимодействия между нижним и верхним проводниками будем искать как сумму четырех сил, обозначение которых понятно из рисунка. Силы отталкивания
. Силу взаимодействия между нижним и верхним проводниками будем искать как сумму четырех сил, обозначение которых понятно из рисунка. Силы отталкивания ![]() и
и ![]() будем брать со знаком минус, а силы притяжения
будем брать со знаком минус, а силы притяжения ![]() и
и ![]() будем брать со знаком плюс.
будем брать со знаком плюс.
Для единичного участка двухпроводной линии силы, действующие между отдельными подсистемами, запишутся
(2.1)
Складывая все силы, получим величину суммарной силы, приходящейся на единицу длины проводника,
(2.2)
В данном выражении в качестве ![]() и
и ![]() взяты абсолютные величины зарядов, а знаки сил учтены в выражении в скобках. Для случая
взяты абсолютные величины зарядов, а знаки сил учтены в выражении в скобках. Для случая ![]() <<
<< ![]() , возьмем только два первых члена разложения в ряд
, возьмем только два первых члена разложения в ряд ![]() , т.е. будем считать, что
, т.е. будем считать, что 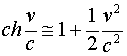 . Из соотношения (2.2) получаем
. Из соотношения (2.2) получаем
(2,3)
где в качестве ![]() и
и ![]() взяты абсолютные величины удельных зарядов, а
взяты абсолютные величины удельных зарядов, а ![]() и
и ![]() берут со своими знаками.
берут со своими знаками.
Поскольку магнитное поле прямого провода, по которому течёт ток ![]() , определяем соотношением
, определяем соотношением
то из соотношения (20.3) получаем:
где ![]() - магнитное поле создаваемое нижним проводником, по которому течёт ток
- магнитное поле создаваемое нижним проводником, по которому течёт ток ![]() , в месте расположения верхнего проводника.
, в месте расположения верхнего проводника.
Аналогично
где ![]() - магнитное поле, создаваемое верхним проводником в районе расположения нижнего проводника.
- магнитное поле, создаваемое верхним проводником в районе расположения нижнего проводника.
Эти соотношения полностью совпадают с результатами, полученными на основании концепции магнитного поля.
Соотношение (2.3) представляет известное правило силового взаимодействия токонесущих систем, но получено оно не феноменологическим путем на основании введения феноменологического магнитного поля, а на основе вполне понятных физических процедур, в предположении того, что скалярный потенциал заряда зависит от скорости. В формировании сил взаимодействия в данном случае непосредственное участие принимает решетка, чего нет в модели магнитного поля. В рассмотренной модели хорошо видны места приложения сил. Полученные соотношения совпадают с результатами, полученными на основе концепции магнитного поля и аксиоматически введённой силой Лоренца. В данном случае взят только первый член разложения в ряд ![]() . Для скоростей
. Для скоростей ![]() ~
~ ![]() следует брать все члены разложения. Этим предлагаемый метод отличается от метода расчёта силовых взаимодействий на основе концепции магнитного поля. Если учесть это обстоятельство, то связь между силами взаимодействия и скоростями зарядов оказывается нелинейной. Это, в частности приводит к тому, что закон силового взаимодействия токонесущих систем является асимметричным. При одинаковых значениях токов, но при разных их направлениях, силы притяжения и отталкивания становятся неодинаковыми. Силы отталкивания оказываются большими, чем силы притяжения. Эта разница невелика и определяется выражением
следует брать все члены разложения. Этим предлагаемый метод отличается от метода расчёта силовых взаимодействий на основе концепции магнитного поля. Если учесть это обстоятельство, то связь между силами взаимодействия и скоростями зарядов оказывается нелинейной. Это, в частности приводит к тому, что закон силового взаимодействия токонесущих систем является асимметричным. При одинаковых значениях токов, но при разных их направлениях, силы притяжения и отталкивания становятся неодинаковыми. Силы отталкивания оказываются большими, чем силы притяжения. Эта разница невелика и определяется выражением
но при скоростях носителей зарядов близких к скорости света она может оказаться вполне ощутимой.
Уберем решетку верхнего проводника (рис. 1), оставив только свободный электронный поток. При этом исчезнут силы ![]() и
и ![]() , и это будет означать взаимодействие нижнего проводника с потоком свободных электронов, движущихся со скоростью
, и это будет означать взаимодействие нижнего проводника с потоком свободных электронов, движущихся со скоростью ![]() на месте расположения верхнего проводника. При этом значение силы взаимодействия определяется как:
на месте расположения верхнего проводника. При этом значение силы взаимодействия определяется как:
(2.4)
Сила Лоренца предполагает линейную зависимость между силой, действующей на заряд, движущийся в магнитном поле, и его скоростью. Однако в полученном соотношении зависимость величины силы от скорости электронного потока будет нелинейной. Из соотношения (2.4) нетрудно видеть, что с ростом ![]() отклонение от линейного закона увеличивается, и в случае, когда
отклонение от линейного закона увеличивается, и в случае, когда ![]() >>
>>![]() , сила взаимодействия стремятся к нулю. Это очень важный результат. Именно этот феномен и наблюдали в своих известных экспериментах Томпсон и Кауфман, когда заметили, что с ростом скорости электронного пучка он хуже отклоняется магнитным полем. Результаты своих наблюдений они связали с ростом массы электрона. Как видим причина здесь другая.
, сила взаимодействия стремятся к нулю. Это очень важный результат. Именно этот феномен и наблюдали в своих известных экспериментах Томпсон и Кауфман, когда заметили, что с ростом скорости электронного пучка он хуже отклоняется магнитным полем. Результаты своих наблюдений они связали с ростом массы электрона. Как видим причина здесь другая.
Отметим ещё один интересный результат. Из соотношения (2.3), с точностью до квадратичных членов, сила взаимодействия электронного потока с прямолинейным проводником, по которому протекает ток, можно определить по следующей зависимости:
(2.5)
Из выражения (2.5) следует, что при однонаправленном движении электронов в проводнике и в электронном потоке сила взаимодействия при выполнении условия 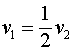 отсутствует.
отсутствует.
Поскольку скорость электронного потока обычно гораздо выше скорости носителей тока в проводнике, то вторым членом в скобках в соотношении (2.5) можно пренебречь. Тогда, поскольку
магнитное поле, создаваемое нижним проводником в месте движения электронного потока, получим:
В данном случае, полученное значение силы в точности совпадает со значением силы Лоренца.
Учитывая, что
можно считать, что на заряд, движущийся в магнитном поле, действует электрическое поле ![]() , направленное нормально к направлению движения заряда. Данный результат также с точностью до квадратичных членов
, направленное нормально к направлению движения заряда. Данный результат также с точностью до квадратичных членов ![]() полностью совпадает с результатами концепции магнитного поля и определяет силу Лоренца, действующую со стороны магнитного поля на поток движущихся электронов.
полностью совпадает с результатами концепции магнитного поля и определяет силу Лоренца, действующую со стороны магнитного поля на поток движущихся электронов.
Как уже было сказано, одним из важных противоречий концепции магнитного поля является то, что два параллельных пучка одноименных зарядов, двигающихся с одинаковой скоростью в одном направлении, должны притягиваться. В данной модели этого противоречия уже нет. Если считать, что скорости зарядов в верхнем и нижнем проводе будут равны, а решетка отсутствует, т.е. оставить только электронные потоки, то останется только сила отталкивания ![]() независимо от того движутся заряды или нет.
независимо от того движутся заряды или нет.
Таким образом, движущийся электронный поток взаимодействует одновременно и с движущимися электронами в нижней проволоке, и с её решеткой, а сумма этих сил взаимодействия и называется силой Лоренца. Эта сила и действует на движущийся поток электронов.
Закономерно возникает вопрос, а создаёт ли магнитное поле сам движущийся поток электронов в отсутствии компенсирующих зарядов решетки или положительных ионов в плазме? Рассмотренная схема показывает, что эффект силового взаимодействия между токонесущими системами требует в обязательном порядке наличия положительно заряженной решетки. Поэтому сам движущийся электронный поток не может создавать того эффекта, который создаётся при его движении в положительно заряженной решетке. В то же время, если рассмотреть два параллельно движущихся потока электронов, то возникает дополнительная сила взаимодействия, зависящая от относительной скорости этих потоков.
Продемонстрируем ещё один подход к проблеме силового взаимодействия токонесущих систем. Констатация факта наличия сил между токонесущими системами указывает на то, что существует какое-то поле скалярного потенциала, градиент которого и обеспечивает указанную силу. Но что это за поле? Соотношение (2.3) даёт только значение силы, но не говорит о том, градиент какого скалярного потенциала эти силы обеспечивает. Будем поддерживать постоянными токи ![]() и
и ![]() , и начнём сближать или удалять проводники. Работа, которая при этом будет затрачена, и есть тот потенциал, градиент которого даёт силу. Проинтегрировав соотношение (2.3) по
, и начнём сближать или удалять проводники. Работа, которая при этом будет затрачена, и есть тот потенциал, градиент которого даёт силу. Проинтегрировав соотношение (2.3) по ![]() , получаем величину энергии:
, получаем величину энергии:
Эта энергия, в зависимости от того удалять проводники друг от друга, или сближать, может быть положительной или отрицательной. Когда проводники удаляют, то энергия положительна, а это означает, что, поддерживая ток в проводниках постоянным, генератор отдаёт энергию. Это явление и лежит в основе работы всех электродвигателей. Если проводники сближаются, то работу совершают внешние силы, над источником, поддерживающим в них постоянство токов. Это явление лежит в основе работы механических генераторов э.д.с.
Соотношение для энергии можно переписать и так:
где
есть ![]() - компонента векторного потенциала, создаваемая нижним проводником в месте расположения верхнего проводника, а
- компонента векторного потенциала, создаваемая нижним проводником в месте расположения верхнего проводника, а
есть ![]() - компонента векторного потенциала, создаваемая верхним проводником в месте расположения нижнего проводника.
- компонента векторного потенциала, создаваемая верхним проводником в месте расположения нижнего проводника.
Рассмотренный подход демонстрирует ту большую роль, которую играет векторный потенциал в вопросах силового взаимодействия токонесущих систем и преобразования электрической энергии в механическую. Такой подход также ясно указывает на то, что сила Лоренца есть следствие взаимодействия токонесущих систем с полем векторного потенциала, создаваемого другими токонесущими системами. И важным обстоятельством является то, что формирование векторного потенциала обязано зависимости скалярного потенциала от скорости. С физической точки зрения это ясно. Движущиеся заряды, в связи с наличием зависимости их скалярного потенциала от скорости, создают скалярное поле, градиент которого и даёт силу. Но создание любого силового поля требует затрат энергии. Эти затраты и совершает генератор, создавая токи в проводниках. При этом в окружающем пространстве создаётся особое поле, которое взаимодействует с другими движущимися зарядами по особым векторным правилам, при которых только скалярное произведение вектора скорости заряда и векторного потенциала даёт потенциал, градиент которого и даёт силу, действующую на движущийся заряд. Это и есть сила Лоренца.
Несмотря на простоту и очевидность такого подхода, этот простой механизм до настоящего времени не был окончательно осознан. По этой причине сила Лоренца до сих пор вводилась в классической электродинамике аксиоматическим путём.
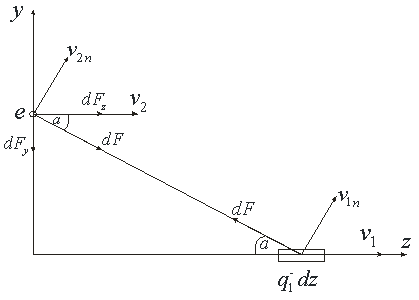
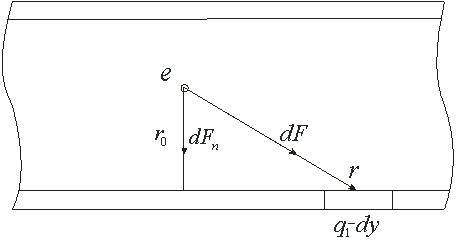
Рассмотрим ещё один случай, когда одиночный отрицательный заряд ![]() движется со скоростью
движется со скоростью ![]() параллельно проводнику, по которому со скоростью
параллельно проводнику, по которому со скоростью ![]() двигаются электроны, удельная плотность которых, приходящаяся на единицу длины провода, составляет
двигаются электроны, удельная плотность которых, приходящаяся на единицу длины провода, составляет ![]() (рис.2).
(рис.2).
Рис. 2. Схема взаимодействия движущегося точечного заряда с проводником, по которому течёт ток.
Будем считать, что проводник до начала движения электронов был электронейтральным и удельная плотность положительных ионов и электронов были равны. Элемент заряда, приходящийся на отрезок ![]() проводника с током, при этом составит
проводника с током, при этом составит ![]() . Элемент силы действия движущегося заряда
. Элемент силы действия движущегося заряда ![]() на элемент
на элемент ![]() определится соотношением:
определится соотношением:
где ![]() и
и ![]() - компоненты соответствующих скоростей, нормальные к радиусу, соединяющему движущийся заряд с элементом заряда
- компоненты соответствующих скоростей, нормальные к радиусу, соединяющему движущийся заряд с элементом заряда ![]() .
.
Поскольку ![]() и
и ![]() , а также, учитывая, что
, а также, учитывая, что ![]()
можно записать:
Полученная сила - это сила притяжения. Элемент этой силы, параллельной ![]() , запишется как:
, запишется как:
(2.6)
а элемент силы, нормальной к ![]() - как:
- как:
(2.7)
Проинтегрировав соотношение (2.6) и учитывая, что ток, текущий по нижнему проводнику определяется соотношением ![]() , запишем силу, действующую на одиночный движущийся заряд
, запишем силу, действующую на одиночный движущийся заряд ![]() со стороны правой части проволоки:
со стороны правой части проволоки:
(2.8)
Если учесть также взаимодействие с левой её частью проволоки, то сила, действующая параллельно ![]() и определяемая соотношением (2.8), удвоится, а силы, действующие по нормали к
и определяемая соотношением (2.8), удвоится, а силы, действующие по нормали к ![]() , компенсируются. Таким образом, суммарная сила, действующая на заряд, движущийся параллельно проволоке, запишется:
, компенсируются. Таким образом, суммарная сила, действующая на заряд, движущийся параллельно проволоке, запишется:
(2.9)
Поскольку магнитное поле, создаваемое нижним проводником с током в точке нахождения движущегося заряда, определяется соотношением
а магнитная проницаемость 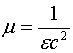 , то из соотношения (2.8) получаем
, то из соотношения (2.8) получаем
Эта сила в точности равна силе Лоренца.
Теперь рассмотрим случай, когда заряд движется между двумя безграничными параллельными пластинами, по которым протекает удельный ток ![]() , приходящийся на единицу ширины пластин (рис. 3). Этот ток течёт по нормали к плоскости рисунка. При этом заряд движется параллельно току, протекающему в пластинах.
, приходящийся на единицу ширины пластин (рис. 3). Этот ток течёт по нормали к плоскости рисунка. При этом заряд движется параллельно току, протекающему в пластинах.
Рис.3. Схема взаимодействия движущегося точечного заряда с токами, текущими по параллельным проводящим пластинам.
Учитывая соотношение (2.9), запишем элемент силы, действующей на движущийся заряд со стороны элемента тока, текущего нормально к элементу ![]()
(2.10)
В этом соотношении ![]() это толщина слоя, по которому течёт ток, а
это толщина слоя, по которому течёт ток, а ![]() - плотность электронов.
- плотность электронов.
Перепишем соотношение (20.10), учитывая что 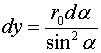 ,
,  , а также то, что
, а также то, что 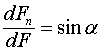 , где
, где ![]() - элемент силы, направленный параллельно
- элемент силы, направленный параллельно ![]() , а
, а ![]() - элемент силы, направленный нормально к
- элемент силы, направленный нормально к ![]() :
:
Проинтегрировав это выражение, получим полную силу, действующую на движущийся заряд со стороны одной полуплоскости:
Учитывая, что в случае, когда элемент ![]() равен единичной длине, выполняется соотношение
равен единичной длине, выполняется соотношение ![]() , а также то, что на заряд действуют силы со стороны четырёх полуплоскостей (две со стороны нижней пластины и две со стороны верхней), окончательно получаем:
, а также то, что на заряд действуют силы со стороны четырёх полуплоскостей (две со стороны нижней пластины и две со стороны верхней), окончательно получаем:
И опять конечный результат в точности совпал с результатами концепции магнитного поля.
Таким образом, результаты, полученные с учётом введения скалярно-векторного потенциала и концепции магнитного поля, полностью совпадают, если учитывать только квадратичные члены разложения гиперболического косинуса в ряд. В случае учёта членов разложения более высоких порядков, когда скорости движения зарядов велики, такого совпадения не будет и связь между силой и скоростью становится нелинейной, и концепция магнитного поля уже не даст правильных результатов.
Достоинством данного метода рассмотрения взаимодействия между токонесущими системами и зарядами является то, что он указывает на конкретные места приложения сил, действующих между их элементами и движущимися зарядами, чего нет в концепции магнитного поля. Рассмотренный подход даёт возможность определить силы взаимодействия между любыми токонесущими системами при любой их конфигурации, и показывает, что такие понятия, как магнитный векторный потенциал и магнитное поле для стационарных процессов это следствие зависимости скалярного потенциала заряда от скорости его движения. В случае же нестационарных процессов, когда возникает ускорение заряда, при решении задачи следует учитывать эффекты запаздывания.
Теперь можно проверить работает ли рассмотренный механизм взаимодействия токонесущих систем в случае длинной линии (рис.4), по которой распространяется электротоковая волна. Напряженность электрического поля между плоскостями линии определяется соотношением:
(2.11)
![]() - заряд, приходящийся на единичный квадрат поверхности длинной линии.
- заряд, приходящийся на единичный квадрат поверхности длинной линии.
Удельный ток, приходящийся на единицу ширины линии, магнитное и электрическое поле в ней связаны соотношением
(2.12)
Из этого соотношения получаем
(2.13)
Рис. 4. Двухпроводная линия, состоящая из двух идеально проводящих плоскостей
Поскольку токи в плоскостях линии направлены в противоположных направлениях, то, учитывая соотношения (2.11 – 2.13), значение силы отталкивания, приходящаяся на единичный квадрат поверхности, запишем:
Таким образом, концепция скалярно-векторного потенциала и в данном случае даёт правильный ответ.
Рассмотрим ещё одно интересное следствие, вытекающее из приведенного рассмотрения. Если в качестве плоскостей длинной линии использовать сверхпроводник, то магнитное поле на его поверхности, равное удельному току, можно определить из соотношения:
(2.14)
где 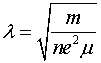 - глубина проникновения магнитного поля в сверхпроводник.
- глубина проникновения магнитного поля в сверхпроводник.
Если подставить значение глубины проникновения в соотношение (2.14), то получим неожиданный результат:
Оказывается, что величина магнитного поля вовсе не зависит от величины зарядов носителей тока, а зависит от их массы.
Таким образом, удельная энергия магнитных полей
(2.15)
равна кинетической энергия движения зарядов, приходящаяся на единицу объёма. Но магнитное поле, связанное с движением носителей тока в поверхностном слое сверхпроводника, существует не только на его поверхности и в скинслое. Объём, занимаемый магнитными полями, несоизмеримо больший, чем объём скинслоя. Если обозначить длину линии, изображённой на рис. 4, как ![]() , то объём скинслоя в сверхпроводящих плоскостях линии составит
, то объём скинслоя в сверхпроводящих плоскостях линии составит ![]() . Энергию магнитных полей в этом объёме определяем из соотношения:
. Энергию магнитных полей в этом объёме определяем из соотношения:
энергия же магнитных полей, накопленная между плоскостями линии, составит:
(2.16)
Если учесть, что глубина проникновения магнитного поля в сверхпроводниках составляет несколько сотен ангстрем, то при макроскопических размерах линии можно считать, что полную энергию магнитных полей в ней определяют соотношением (2.16).
Поэтому, образование магнитных полей ![]() между плоскостями линии, которые возникают в связи с движением зарядов в скинслое, требует таких же затрат энергии, как если бы весь объём линии был заполнен частицами, движущимися со скоростью
между плоскостями линии, которые возникают в связи с движением зарядов в скинслое, требует таких же затрат энергии, как если бы весь объём линии был заполнен частицами, движущимися со скоростью ![]() , плотность которых и масса составляют соответственно
, плотность которых и масса составляют соответственно ![]() и
и ![]() .
.
Очевидно, что эффективная масса электрона по сравнению с массой свободного электрона возрастает при этом в ![]() раз. Это является следствием того, что механическое движение электронов приводит не только к накоплению их кинетической энергии в скинслое, но, ввиду зависимости их скалярного потенциала от скорости, в линии происходит также накопление потенциальной энергии, градиент которой даёт силу, действующую на проводящие плоскости линии. Таким образом, становится понятной природа таких параметров как индуктивность и эффективная масса электрона, которые в данном случае зависят, в основном, не от массы свободных электронов, а от конфигурации проводников, по которым эти электроны двигаются.
раз. Это является следствием того, что механическое движение электронов приводит не только к накоплению их кинетической энергии в скинслое, но, ввиду зависимости их скалярного потенциала от скорости, в линии происходит также накопление потенциальной энергии, градиент которой даёт силу, действующую на проводящие плоскости линии. Таким образом, становится понятной природа таких параметров как индуктивность и эффективная масса электрона, которые в данном случае зависят, в основном, не от массы свободных электронов, а от конфигурации проводников, по которым эти электроны двигаются.
Основы униполярной индукции в концепции зависимости скалярного потенциала заряда от его относительной скорости
Рассмотрим случай, когда имеется одиночный длинный проводник, по которому течёт ток. Будем по-прежнему считать, что в проводнике имеется система взаимно вложенных зарядов положительной решетки ![]() и свободных электронов
и свободных электронов ![]() , которые в отсутствие тока нейтрализуют друг друга (рис.5).
, которые в отсутствие тока нейтрализуют друг друга (рис.5).
Рис. 5. Проводник, по которому течёт ток.
Электрическое поле, создаваемое неподвижной решеткой в зависимости от расстояния ![]() от центра проводника, который расположен по оси
от центра проводника, который расположен по оси ![]() имеет вид
имеет вид
(3.4)
При этом считается, что направление вектора электрического поля совпадает с направлением ![]() . Если электронный поток движется со скоростью
. Если электронный поток движется со скоростью ![]() , то электрическое поле этого потока определяется равенством:
, то электрическое поле этого потока определяется равенством:
(2.5)
Складывая (2.4) и (2.5), получаем:
Это означает, что вокруг проводника с током имеется электрическое поле, соответствующее отрицательному заряду проводника. Однако это поле имеет очень незначительную величину, поскольку в реальных проводниках ![]() <<
<<![]() . Это поле может быть обнаружено только при плотностях токов, которые могут быть достигнуты в сверхпроводниках, что экспериментально подтверждено в работах [5,6].
. Это поле может быть обнаружено только при плотностях токов, которые могут быть достигнуты в сверхпроводниках, что экспериментально подтверждено в работах [5,6].
Рассмотрим случай, когда проводник, по которому со скоростью ![]() текут электроны, движется в обратном направлении со скоростью
текут электроны, движется в обратном направлении со скоростью ![]() (Рис. 6). В этом случае соотношения (3.4) и (3.5) примут вид:
(Рис. 6). В этом случае соотношения (3.4) и (3.5) примут вид:
(3.6)
Рис.6. Движущийся проводник с током.
(3.7)
Складывая (3.6) и (3.7), получаем:
(3.8)
В данном соотношении в качестве удельного заряда взята его абсолютная величина. Поскольку скорость механического движения проводника значительно больше, чем дрейфовая скорость электронов, вторым членом в скобках можно пренебречь. При этом из (3.8) получаем
(3.9)
Полученный результат означает, что вокруг движущегося проводника, по которому течёт ток, образуется электрическое поле, определяемое соотношением (3.9), что равнозначно появлению на этом проводнике удельного положительного заряда равного
Если проводник свернуть в кольцо и вращать его так, чтобы линейная скорость его частей была равна ![]() , то вокруг такого кольца появится электрическое поле, соответствующее наличию на кольце указанного удельного заряда. Но это означает, что вращающийся виток, который и является вращающимся магнитом, приобретает удельный электрический заряд на самой проволоке, из которой он состоит. При движении линейного проводника с током электрическое поле будет наблюдаться по отношению к неподвижному наблюдателю, но если наблюдатель будет двигаться вместе с проводником, то такие поля будут отсутствовать.
, то вокруг такого кольца появится электрическое поле, соответствующее наличию на кольце указанного удельного заряда. Но это означает, что вращающийся виток, который и является вращающимся магнитом, приобретает удельный электрический заряд на самой проволоке, из которой он состоит. При движении линейного проводника с током электрическое поле будет наблюдаться по отношению к неподвижному наблюдателю, но если наблюдатель будет двигаться вместе с проводником, то такие поля будут отсутствовать.
Возникает вопрос, можно ли при помощи таких полей в цепи, неподвижной по отношению к движущемуся проводнику, получить э.д.с. Этот вопрос равноценен вопросу, а можно ли с помощью электрических полей заряженного конденсатора получить э.д.с. Очевидно нельзя, поскольку такие поля являются потенциальными, и движение в них заряда по замкнутому контуру даёт нулевую работу. Электрические поля, полученные при движении проводника с током тоже являются потенциальными и размещение в них любого контура не даст на его концах разности потенциалов. Но тогда как получается униполярная индукция, при которой на неподвижных контактах получается разность потенциалов. Это легко понять из рис. 7.
Рис. 7. Схема формирования э.д.с. униполярной индукции.
Будем считать, что ![]() и
и ![]() координаты точек касания подвижных контактов, которые скользят по металлической пластине, движущейся совместно с проводником, по которому течёт ток. Эти контакты подключены к вольтметру, который также неподвижен. Тогда, можно вычислить разность потенциалов между этими контактами, проинтегрировав соотношение (3.9):
координаты точек касания подвижных контактов, которые скользят по металлической пластине, движущейся совместно с проводником, по которому течёт ток. Эти контакты подключены к вольтметру, который также неподвижен. Тогда, можно вычислить разность потенциалов между этими контактами, проинтегрировав соотношение (3.9):
Но чтобы к нагрузке, в данном случае к вольтметру, приложить эту разность потенциалов, необходимо скользящие контакты замкнуть перемычкой, на которой нет указанной разности потенциалов. Но поскольку металлическая пластина движется совместно с проводником, то на ней разность потенциалов отсутствует. Она и служит той перемычкой, которая даёт возможность превратить такой составной контур в источник э.д.с. по отношению к вольтметру.
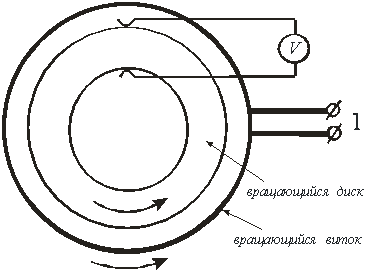
Теперь можно проволоку свернуть в кольцо (рис. 8) из одного или нескольких витков, и запитать его от источника тока. Причём контакты 1 следует вывести на кольцевые коллекторы, находящиеся на оси вращения и к ним присоединить трущиеся неподвижные щётки. Таким образом, можно получить вращающийся магнит. В этот магнит следует поместить проводящий диск с отверстием (рис. 7), вращающийся совместно с витками магнита, и при помощи неподвижных контактов, скользящим по образующим диска, подать напряжение на вольтметр. В качестве предельного случая можно взять сплошной металлический диск и подключить скользящие контакты к образующей диска и его оси. Вместо вращающегося витка с током можно взять диск, намагниченный в осевом направлении, который эквивалентен витку с током, при этом будет получен такой же эффект.
Рис. 8. Схема униполярного генератора с вращающимся магнитом и вращающимся проводящим диском.
Возможны различные сочетания вращающихся магнитов и дисков Ниже дана таблица, приведенная в Википедии
http://ru.wikipedia.org/wiki/%D0%A3%D0%BD%D0%B8%D0%BF%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%B3%D0%B5%D0%BD%D0%B5%D1%80%D0%B0%D1%82%D0%BE%D1%80, после которой следует утверждение, что последовательное объяснение униполярной индукции даётся теорией относительности.
| Первый столбец | магнит | диск | внешняя цепь | есть ли напряжение? |
|---|---|---|---|---|
| 1 | неподвижен | неподвижен | неподвижен | отсутствует |
| 2 | неподвижен | вращается | неподвижен | есть |
| 3 | неподвижен | неподвижен | вращается | есть |
| 4 | неподвижен | вращается | вращается | не определено |
| 5 | вращается | неподвижен | неподвижен | отсутствует |
| 6 | вращается | вращается | неподвижен | есть |
| 7 | вращается | неподвижен | вращается | есть |
| 8 | вращается | вращается | вращается | не определено |
Мы рассмотрели самый непонятный случай (позиция 6), касающийся униполярной индукции, и ниже покажем, что при помощи указанной методики элементарно рассматриваются все возможные конфигурации униполярных генераторов, приведенных в таблице.
Рассмотрим их последовательно.
Первая позиция комментариям не подлежит, т.к. все элементы неподвижны. Вторая позиция характеризуется следующей схемой:
Рис. 9. Случай неподвижного магнита и вращающегося диска.
Эту схему характеризуют следующие соотношения:
электрическое поле, генерируемое во вращающемся диске движущимися электронами определяется соотношением
а неподвижными ионами
Суммарная напряженность электрического поля при этом составит
а разность потенциалов между точками ![]() и
и ![]() в системе координат, движущейся вместе с пластиной, будет равна
в системе координат, движущейся вместе с пластиной, будет равна
Поскольку в неподвижной по отношению к магниту цепи вольтметра индуцированная разность потенциалов отсутствует, то указанная разность потенциалов и будет равна э.д.с. рассмотренного генератора. Как и ранее движущуюся проводящую пластинку можно свернуть в диск с отверстием, а проволоку, по которой течёт ток в кольцо с током, которое является эквивалентом магнита, намагниченного в торцевом направлении.
Третий вариант из таблицы эквивалентен второму с той лишь разницей, что движущаяся цепь вольтметра и неподвижный диск меняются местами.
По четвёртому варианту напряжение на клеммах вольтметра будет отсутствовать, т.к. и диск и цепь вольтметра двигаются с одинаковой скоростью и в них генерируются встречные значения разности потенциалов одинаковые по величине, которые друг друга компенсируют. То же относится и к пятому варианту.
Шестой вариант, как наиболее сложный, мы рассмотрели в самом начале.
Седьмой вариант характеризуется теми же соотношениями, что и шестой с той лишь разницей, что цепь вольтметра и диск меняются местами.
По восьмому варианту э.д.с. не будет, т.к. и в диске и в цепи вольтметра будет индуцироваться одинаковая, но встречная разность потенциалов.
Таким образом, мы исчерпали все варианты, приведенные в таблице, но за кадром остался случай, когда вращающийся магнит выполнен из проводящего материала, собственно тот униполярный генератор, который и исследовал Фарадей. Данный случай относится к шестому варианту с той лишь разницей, что вращающийся магнит и проводящий диск совмещены в одном элементе.
Таким образом, концепция зависимости скалярного потенциала заряда от относительной скорости даёт ответы на все поставленные вопросы и СТО здесь не нужна.
Заключение
Данный пример показывает, насколько мало продвинулась электродинамика за время своего существования. Явление электромагнитной индукции Фарадей открыл в 1831 г. и уже почти 200 лет его учение не претерпело практически никаких изменений, и физические причины самых элементарных электродинамических явлений так до сих пор и не поняты. Конечно, для своего времени Фарадей был гением, но что делали физики после него? Были ещё такие гениальные фигуры как Максвелл и Герц, но даже они не понял, что основой всей классической электродинамики является зависимость скалярного потенциала заряда от его относительной скорости, и что это тот основополагающий закон, из которого следуют все остальные её законы.
Список литературы
- 1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. В 9-и т. - М.: Мир, 1977.- т.6.- 347 с.
- 2. Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967, - 664 - с.
- 3. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 4. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков,
Константа, 2003.- 72 с. ISBN – 966-7983-55-2.
- 5. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 6. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- 7. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 8. Mende F. F. Experimental corroboration and theoretical interpretation of dependence of charge value on DC flow velocity through superconductors. Proceedings International Conference “Physics in Ukraine”, Kiev, 1993.
- 9. Mende F. F. Conception of the scalar-vector potential in contemporary electrodynamics, arXiv, physics/0506083.