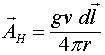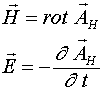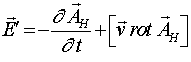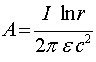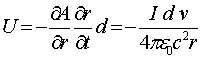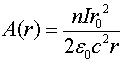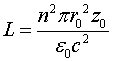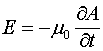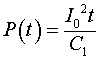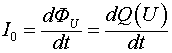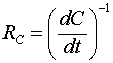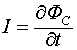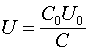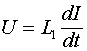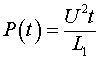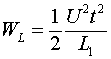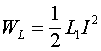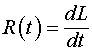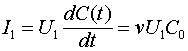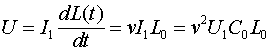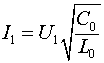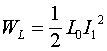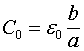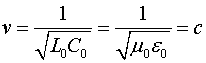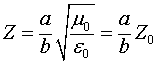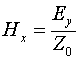Электрическая и электромеханическая индукция
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
- 1 Введение
- 2 Полный закон индукции Фарадея
- 3 Законы взаимной индукции между проводниками
- 4 Недоразумения в классической электродинамике, связанные с объяснением полей индукции вблизи длинного соленоида
- 5 Законы самоиндукции
- 6 Новый способ получения волнового уравнения
- 7 Переходные процессы в отрезках длинных линий
- 8 Список литературы
Введение
Электродинамика существует уже более 200 лет и справедливости ради следует сказать, что очень многие задачи она решает вполне достойно. Известно, что эта наука является феноменологической и основывается на опытных и экспериментальных данных. Но пока попытка найти адекватное математическое описание многих электродинамических явлений наталкивается на трудности, связанные, прежде всего, с непониманием самой физики происходящего. Если посмотреть труды маститых теоретиков, то можно заметить, что это непонимание имеет место даже на уровне обычных классических представлений. Например, тот же Левич, вводя понятие обобщённого импульса движущегося заряда, путает потенциальную и кинетическую энергию[1]. Теоретики не понимают, что изменение эффективной массы электрона связано не с тем, что действительно растёт его масса, а с тем, что электрон обладает дополнительной потенциальной энергией, связанной с движением в поле других заряженных частиц [2]. Ландау перепутал интеграл и производную гармонической функции и в своих трудах вводит метафизическое понятие диэлектрической проницаемости плазмы, которая зависит от частоты [3]. Но введение такого понятия означает признание возможности создания вечного двигателя [4]. До конца не понятна роль векторного потенциала и источников его формирования, в то время как это один из важнейших потенциалов, от которого зависит не только силовое взаимодействие токонесущих систем, но и процессы излучения.
Задачей любого физика является, прежде всего, понимание физики процессов, а потом уже нахождение адекватного математического аппарата для описания этих процессов. Но это физическое понимание часто отсутствует даже у таких известных теоретиков как Ландау и Левич, с чем и связаны допущенные ими ошибки.
Главным законом индукции в электродинамике является закон Фарадея, но и из этого закона имеются исключения, под этот закон не подпадает принцип действия униполярного генератора, который считается исключением из правила потока. Но ведь физика это не грамматика, и если из какого-то физического закона имеются исключения, то этот закон или не верен или не полон. Вот что пишет по этому поводу Фейнман [5]: “...”правило потока”, согласно которому э.д.с. в контуре равна взятой с обратным знаком скорости, с которой меняется магнитный поток через контур, когда поток меняется за счет изменения поля или когда движется контур (или когда происходит и то, и другое). Две возможности – “контур движется” или “поле меняется” – неразличимы в формулировке правила. Тем не менее, для объяснения правила в этих двух случаях мы пользовались двумя совершенно различными законами: ![]() для “движущегося контура” и
для “движущегося контура” и 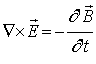 для “меняющегося поля”. И далее: “Мы не знаем в физике ни одного такого примера, когда бы простой и точный общий закон требовал для своего настоящего понимания анализа в терминах двух различных явлений. Обычно столь красивое обобщение оказывается исходящим из единого глубокого основополагающего принципа. Но в этом случае какого-либо особо глубокого принципа не видно”. Пожалуй, общепринятой является и такая трактовка закона Фарадея, которая содержится в работе [5]. “Наблюдения Фарадея привели к открытию нового закона о связи электрического и магнитного полей: в области, где магнитное поле меняется со временем, генерируется электрическое поле”. Однако, и из этого правила также имеется исключение, правда, названные источники об этом умалчивают. Действительно, вне очень длинного соленоида магнитные поля отсутствуют, однако, при изменении тока в таком соленоиде вне соленоида генерируются электрические поля.
для “меняющегося поля”. И далее: “Мы не знаем в физике ни одного такого примера, когда бы простой и точный общий закон требовал для своего настоящего понимания анализа в терминах двух различных явлений. Обычно столь красивое обобщение оказывается исходящим из единого глубокого основополагающего принципа. Но в этом случае какого-либо особо глубокого принципа не видно”. Пожалуй, общепринятой является и такая трактовка закона Фарадея, которая содержится в работе [5]. “Наблюдения Фарадея привели к открытию нового закона о связи электрического и магнитного полей: в области, где магнитное поле меняется со временем, генерируется электрическое поле”. Однако, и из этого правила также имеется исключение, правда, названные источники об этом умалчивают. Действительно, вне очень длинного соленоида магнитные поля отсутствуют, однако, при изменении тока в таком соленоиде вне соленоида генерируются электрические поля.
До настоящего времени классическая электродинамика разделена на две не связанные между собой части. В уравнениях Максвелла не содержится информация о силовом взаимодействии токонесущих систем, а сила Лоренца, которая определяет такое взаимодействие, вводится как отельный экспериментальный постулат. Поэтому сама электродинамика состоит как бы из двух не связанных между собой частей. С одной стороны это уравнения Максвелла, которые дают возможность получить волновое уравнение для электромагнитных волн, а с другой – постулат о силе Лоренца, позволяющий вычислять силовое взаимодействие токонесущих систем. Магнитная часть силы Лоренца определяется соотношением
Но с физической точки зрения этот экспериментальный постулат представляет нонсенс. Для статических систем сила является градиентом скалярного потенциала, а для прямолинейного движения механической системы она всегда направлена вдоль вектора скорости. В данном же случае сила, действующая на заряд, нормальна к направлению движения и поэтому не совершает работу. Это что новый закон физики, или неправильное понимание постулата?
Полный закон индукции Фарадея
В современных публикациях по электродинамике закон Фарадея записывается следующим образом:
(1.1)
где ![]() - поток магнитной индукции,
- поток магнитной индукции, ![]() - вектор магнитной индукции, а
- вектор магнитной индукции, а ![]() - магнитная проницаемость среды.
- магнитная проницаемость среды.
Данное соотношение предполагает, что поток магнитной индукции может меняться только за счет его изменений во времени. Но поток может меняться и за счёт движения в поле пространственно меняющегося магнитного поля. И если это учесть, то можно переписать закон Фарадея в уточненном виде:
(1.2)
Уточнение закона, вернее его записи, касается лишь того обстоятельства, что если определятся контурный интеграл в движущейся (штрихованной) системе координат, то около ![]() и
и ![]() должны стоять штрихи. Если же контурный интеграл определяется в неподвижной системе координат, то штрихи около
должны стоять штрихи. Если же контурный интеграл определяется в неподвижной системе координат, то штрихи около ![]() и
и ![]() отсутствуют, но при этом справа в выражении (1.2) должна стоять частная производная по времени. Обычно это обстоятельство в литературе не оговаривается.
отсутствуют, но при этом справа в выражении (1.2) должна стоять частная производная по времени. Обычно это обстоятельство в литературе не оговаривается.
Полная производная по времени в соотношении (1.2) означает независимость конечного результата возникновения э.д.с. в контуре от способа изменения потока, т.е. поток может изменяться, как за счет чисто временных изменений ![]() , так и за счет того, что система, в которой измеряется
, так и за счет того, что система, в которой измеряется ![]() , двигается в пространственно меняющемся поле
, двигается в пространственно меняющемся поле ![]() . В соотношении (1.2)
. В соотношении (1.2)
(1.3)
где магнитная индукция определена в неподвижной системе координат, а элемент ![]() – в движущейся системе. Учитывая (1.3), из (1.2) получаем
– в движущейся системе. Учитывая (1.3), из (1.2) получаем
(1.4)
(1.5)
В данном случае контурный интеграл берется по контуру ![]() , охватывающему площадку
, охватывающему площадку ![]() . Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е.
. Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е. ![]() и
и ![]() . Поскольку
. Поскольку ![]() , из (1.5) следует хорошо известный результат:
, из (1.5) следует хорошо известный результат:
(1.6)
из которого следует, что при движении в магнитном поле возникает дополнительное электрическое поле, определяемое последним слагаемым соотношения (1.6). Заметим, что это соотношение мы получили не из преобразований Лоренца, а всего лишь несколько уточнив закон Фарадея. Таким образом, сила Лоренца является следствием такого уточненного закона, а не постулатом, как считалось ранее.
Из соотношения (1.6) следует, что при движении в магнитном поле на заряд действует сила перпендикулярная направлению движения. Однако, физическая природа этой силы нигде не рассматривается. Именно с этим и связана та путаница, которая имеет место при объяснении принципа действия униполярного генератора, а также невозможность объяснения с точки зрения уравнений Максвелла возникновения электрических полей вне бесконечно длинного соленоида.
Закон Ампера, выраженный в векторной форме, определяет магнитное поле в точке наблюдения в следующем виде:
где ![]() - ток в элементе
- ток в элементе ![]() ,
, ![]() - вектор, направленный из
- вектор, направленный из ![]() в точку наблюдения (рис. 1).
в точку наблюдения (рис. 1).
Можно показать, что
и, кроме того, что
Рис. 1. Формирование векторного потенциала элементом проводника ![]() , по которому течёт ток
, по которому течёт ток ![]() .
.
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
где
векторный потенциал магнитного поля.
Замечательным свойством этого выражения является то, что зависимость векторного потенциал обратно пропорциональна расстоянию до точки наблюдения, что характерно для законов излучения.
Поскольку ![]() , где
, где ![]() количество зарядов, приходящееся на единицу длины проводника, то
количество зарядов, приходящееся на единицу длины проводника, то
Если размер элемента ![]() , по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом
, по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом ![]() , по которому течёт ток
, по которому течёт ток ![]() , имеет вид
, имеет вид
Для выяснения физической природы появления последнего слагаемого в соотношении (1.6) запишем ![]() и
и ![]() через магнитный векторный потенциал:
через магнитный векторный потенциал:
(1.7)
Тогда соотношение (1.6) можно переписать
(1.8)
и далее:
(1.9)
Первые два члена правой части равенства (1.9) можно собрать в полную производную векторного потенциала по времени, а именно:
(1.10)
Из соотношения (1.9) видно, что напряженность электрического поля, а следовательно и сила, действующая на заряд, состоит из трех частей.
Первая из них обязана чисто временным изменениям магнитного векторного потенциала. Смысл второго слагаемого правой части соотношения (1.9) тоже понятен. Оно связано с изменением векторного потенциала, но уже за счет того, что заряд движется в пространственно меняющемся поле этого потенциала. Иная природа последнего слагаемого правой части соотношения (1.9). Оно связано с наличием потенциальных сил, т.к. потенциальная энергия заряда, движущегося в поле потенциала ![]() со скоростью
со скоростью ![]() , равна
, равна ![]() . Величина
. Величина ![]() дает силу, точно так же, как дает силу градиент скалярного потенциала. Таким образом, чтобы иметь силу, действующую на заряд, совсем не обязательно иметь изменение потока магнитной индукции через какой-то контур, а можно двигать заряд вдоль вектора векторного потенциала. Этот принцип и лежит в основе работы униполярного генератора. Таким образом, говорить об униполярном генераторе как об “исключении из правила потока” нельзя, т.к. правило потока, как мы видим, это совокупность всех трех составляющих.
дает силу, точно так же, как дает силу градиент скалярного потенциала. Таким образом, чтобы иметь силу, действующую на заряд, совсем не обязательно иметь изменение потока магнитной индукции через какой-то контур, а можно двигать заряд вдоль вектора векторного потенциала. Этот принцип и лежит в основе работы униполярного генератора. Таким образом, говорить об униполярном генераторе как об “исключении из правила потока” нельзя, т.к. правило потока, как мы видим, это совокупность всех трех составляющих.
Соотношение (1.9) дает возможность физически объяснить все составляющие напряженности электрического поля, возникающего в неподвижной и движущейся систем координат.
Беря ротор от обеих частей равенства (1.10) и учитывая, что ![]() , получаем
, получаем
(1.11)
Если движения нет, то соотношение (1.11) превращается в первое уравнение Максвелла. Конечно, по своей информативности соотношение (1.11) сильно уступает соотношению (1.2), т.к. в связи с тем, что ![]() , в нем отсутствует информация о потенциальных силах, обозначенных через
, в нем отсутствует информация о потенциальных силах, обозначенных через ![]() . Поэтому, если нас интересуют все составляющие электрических полей, действующих на заряд, как в неподвижной, так и в движущейся системах координат, мы должны пользоваться соотношением (1.2).
. Поэтому, если нас интересуют все составляющие электрических полей, действующих на заряд, как в неподвижной, так и в движущейся системах координат, мы должны пользоваться соотношением (1.2).
Подводя предварительный итог, можно сказать, что при более внимательном рассмотрении закона Фарадея (1.2) можно достаточно ясно понять все особенности работы униполярного генератора, можно также утверждать, что принцип действия униполярного генератора не является исключением из правила потока (1.2), а является его следствием. Утверждение Фейнмана о том, что правило ![]() для “движущегося контура” и
для “движущегося контура” и  для “меняющегося поля” являются двумя совершенно различными законами не соответствует действительности. Как раз тем единым основополагающим принципом, на отсутствие которого указывает Фейнман, и является закон Фарадея, записанный в полных производных.
для “меняющегося поля” являются двумя совершенно различными законами не соответствует действительности. Как раз тем единым основополагающим принципом, на отсутствие которого указывает Фейнман, и является закон Фарадея, записанный в полных производных.
Таким образом, следует заключить, что движущийся или неподвижный заряд взаимодействует не с магнитным полем, а с полем магнитного векторного потенциала, и только знание этого потенциала и его эволюции дают возможность вычислить все составляющие сил, действующих на заряды. Магнитное же поле является всего лишь пространственной производной такого векторного поля и в некоторых случаях упрощает вычисления.
Законы взаимной индукции между проводниками
Если на единицу длины бесконечно длинного проводника приходится удельный заряд ![]() свободных носителей тока, движущихся со скоростью
свободных носителей тока, движущихся со скоростью ![]() , то по такому проводнику течёт ток
, то по такому проводнику течёт ток ![]() (рис. 2).
(рис. 2).
Рис. 2. Схема формирования векторного потенциала и электрических полей индукции.
Зависимость векторного потенциала от координаты ![]() при этом имеет вид:
при этом имеет вид:
Если величина тока, текущего по проводнику, будет зависеть от времени, то векторный потенциал также будет зависеть от времени. Следовательно, вблизи проводника будет генерироваться электрическое поле. Это поле наведёт э.д.с. в участке неподвижного контура ![]() , параллельного проводнику, и на его клеммах появится напряжение
, параллельного проводнику, и на его клеммах появится напряжение
Это процесс электрической взаимной индукции, при котором индуцируемый ток в неподвижном участке ![]() имеет противоположное направление по отношению к току, текущему в проводнике. Этот эффект используется в трансформаторах.
имеет противоположное направление по отношению к току, текущему в проводнике. Этот эффект используется в трансформаторах.
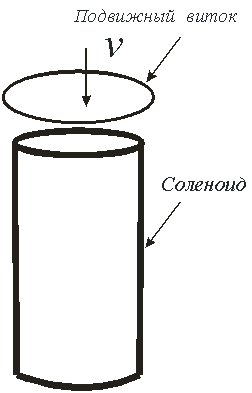
Но ток в указанном участке контура можно возбудить и другим путём. Для этого следует начать удалять или приближать контур к проводнику. Если контур будет двигаться с постоянной скорость, как показано на рисунке, то изменение во времени векторного потенциала будет происходить за счёт того, что векторный потенциал зависит от ![]() . При этом напряжение на клеммах будет определяться соотношением
. При этом напряжение на клеммах будет определяться соотношением
Этот же эффект будет наблюдаться, когда в осевом направлении к кольцу с током приближать или удалять другое кольцо. Этот же эффект будет наблюдаться если на один из концов соленоида с током одевать или снимать индукционный виток (рис. 3). Если в разрыв этого витка включить вольтметр, то при движении витка показания вольтметра будут меняться. Причём вольтметр будет давать показания только в те моменты времени, когда виток будет проходить те участки, где имеется пространственное изменение векторного потенциала, т.е. вблизи торца соленоида. Если же виток, обхватывающий соленоид, двигать вдоль его витков вдали от конца соленоида, то вольтметр реагировать на такое движение не будет.
Случаи с движущимся индукционным контуром вблизи проводника и с подвижным витком вблизи соленоида относятся к электромеханической индукции, поскольку связаны с возникновением индукционных токов при наличии движения индукционных элементов. Именно этот эффект используется во всех электрогенераторах.
Рис. 3. Подвижный виток вблизи конца соленоида.
Недоразумения в классической электродинамике, связанные с объяснением полей индукции вблизи длинного соленоида
В двух предыдущих разделах был рассмотрен новый подход в рассмотрении индукционных процессов, где было показана роль векторного потенциала в этих процессах. К сожалению, до появления работ [6,7] такие подходы к вопросам индукции нигде не рассматривались. Это повлекло за собой ряд принципиальных ошибок, допущенных в ряде учебных пособий по электродинамике. В работе [5] утверждается, что вокруг длинного соленоида, по которому течёт ток, имеются кольцевые линии магнитного векторного потенциала и что якобы в экспериментах Аронова и Бома, в которых в качестве соленоида использовались микроскопические намагниченные ферромагнитные цилиндры, такой потенциал был обнаружен.
Именно с наличием такого потенциала вокруг длинного соленоида и связывают в настоящее время появление индукционных токов в витках, охватываемых такой соленоид. Но на пути такого объяснения имеется существенное препятствие.
Фарадей установил закон индукции, проводя эксперименты на соленоидах, включая и выключая в них ток, или двигая по отношению к соленоидам, через которые протекал постоянный ток, витки проволоки, к которым подключался гальванометр. Его точка зрения, которая считается верной и сегодня, сводилась к тому, что если к соленоиду подключён источник постоянного напряжения ![]() , то ток во всех его витках нарастает по линейному закону
, то ток во всех его витках нарастает по линейному закону
(3.1)
где ![]() - индуктивность соленоида.
- индуктивность соленоида.
Следовательно, магнитное поле при такой интерпретации на всём протяжении соленоида будет нарастать синхронно. Но такой подход означает возможность передачи информации с бесконечной скоростью, т.к. одно и то же магнитное поле возникает одновременно на протяжении сколь угодно длинного соленоида.
Существующая точка зрения наталкивается и на ещё одно препятствие. Значение векторного потенциала в пространстве, окружающем соленоид, находится из соотношения
(3.2)
где ![]() - количество витков, приходящееся на единицу длины соленоида,
- количество витков, приходящееся на единицу длины соленоида, ![]() - ток, текущий через соленоид,
- ток, текущий через соленоид, ![]() - диаметр соленоида,
- диаметр соленоида, ![]() - расстояние от оси соленоида до точки наблюдения. При записи этого соотношения предполагается, что
- расстояние от оси соленоида до точки наблюдения. При записи этого соотношения предполагается, что ![]() .
.
Индуктивность соленоида определяется выражением
(3.3)
Если к соленоиду подключить источник постоянного напряжения ![]() , то с учётом соотношений (3.1 – 3.3), получаем
, то с учётом соотношений (3.1 – 3.3), получаем
где ![]() - общее число витков в соленоиде, а поскольку
- общее число витков в соленоиде, а поскольку
то напряжённость электрического поля в окрестности соленоида в момент подключения к нему источника постоянного напряжения составит
Указанная напряжённость электрического поля в соответствии с рассматриваемой версией возникает в момент подключения к соленоиду источника питания мгновенно на всём его протяжении. Если у соленоида отсутствует сопротивление, то напряжённость электрического поля будет неизменной за весь период времени подключения к соленоиду источника постоянного напряжения. Какие здесь возникают противоречия? Во-первых, электрические поля обладают энергией, и возникать мгновенно не могут. Второе противоречие вытекает из первого и заключается в том, что, поскольку электрические поля обладают энергией, то эта энергия должна включаться в общую энергию, накопленную в соленоиде. Но при расчёте такой энергии учитываются только магнитные поля внутри соленоида.
Таким образом, сам процесс индукции электрических полей вокруг длинного соленоида не может происходить так, как это представлено в существующей литературе [5], когда считается, что циркуляция магнитного векторного потенциала на всём его протяжении возрастает одновременно, что и приводит к индукции э.д.с. в охватывающем витке.
Из сказанного можно заключить, что точка зрения о возникновении электрических полей индукции вокруг соленоида в том месте, где ротор векторного потенциала равен нулю, не соответствует действительности, а сам процесс формирования векторного потенциала снаружи соленоида и магнитных полей внутри него не соответствует тем представлениям, которые существуют на сегодняшний день. Ротор векторного потенциала снаружи соленоида равен нулю, и такое поле не обладает никакой энергией, поэтому и обнаружить его в статическом режиме не представляется возможным. По этой причине эксперименты Аронова и Бома следует считать ошибочными.
Законы самоиндукции
К законам самоиндукции следует отнести те законы, которые описывают реакцию таких элементов радиотехнических цепей, как ёмкость, индуктивность и сопротивление при гальваническом подключении к ним источников тока или напряжения. Эти законы являются основой теории электрических цепей.
Движение зарядов в какой-либо цепи связано с потреблением энергии от источников питания, которые заставляют их менять своё местоположение или двигаться. Процессы взаимодействия источников питания с такими структурами регулируются законами самоиндукции.
Еще раз уточним само понятие самоиндукции. Под самоиндукцией будем понимать реакцию материальных структур с неизменными параметрами на подключение к ним источников напряжения или тока. К самоиндукции отнесём также тот случай, когда при наличии подключенного источника питания или накопленной в системе энергии могут меняться ее параметры. Такую самоиндукцию будем называть параметрической. В дальнейшем будем использовать такие понятия: как генератор тока и генератор напряжения. Под идеальным генератором напряжения будем понимать такой источник, который обеспечивает на любой нагрузке заданное напряжение, внутреннее сопротивление у такого генератора равно нулю. Под идеальным генератором тока будем понимать такой источник, который обеспечивает в любой нагрузке заданный ток, внутреннее сопротивление у такого генератора равно бесконечности. Идеальных генераторов тока и напряжения в природе не существует, поскольку и генераторы тока и генераторы напряжения имеют свое внутреннее сопротивление, которое и ограничивает их возможности.
Если к тому или другому элементу цепи подключить генератор тока или напряжения, то ответной реакцией такого элемента является противодействие изменению своего начального состояния и это противодействие всегда равно приложенному действию, что соответствует третьему закону Ньютона.
Ёмкостная самоиндукция
Если в нашем распоряжении имеется емкость ![]() , и эта емкость заряжена до разности потенциалов
, и эта емкость заряжена до разности потенциалов ![]() , то заряд
, то заряд ![]() , накопленный в емкости, определяется соотношением:
, накопленный в емкости, определяется соотношением:
(4.1.1)
Заряд ![]() , зависящий от величины ёмкости конденсатора и от разности потенциалов на нём, будем называть ещё потоком ёмкостной самоиндукции.
, зависящий от величины ёмкости конденсатора и от разности потенциалов на нём, будем называть ещё потоком ёмкостной самоиндукции.
Когда речь идет об изменении заряда, определяемого соотношением (4.1.1), то эта величина может изменяться путем изменения разности потенциалов при постоянной емкости, или изменением самой емкости при постоянной разности потенциалов, или и того и другого параметра одновременно. Если величина емкости или разности потенциалов на ёмкости зависят от времени, то величина тока определяется соотношением:
Это выражение определяет закон ёмкостной самоиндукции. Таким образом, ток в цепи, содержащей конденсатор, можно получить двумя способами, изменяя напряжение на конденсаторе при постоянной его ёмкости или изменяя саму ёмкость при неизменном напряжении на конденсаторе, или производить изменение обоих параметров одновременно.
Для случая, когда емкость ![]() постоянна, получаем известное выражение для тока, текущего через емкость:
постоянна, получаем известное выражение для тока, текущего через емкость:
(4.1.2)
В том случае, если изменяется емкость, и на ней поддерживается неизменное напряжение ![]() , имеем:
, имеем:
(4.1.3)
Этот случай относиться к параметрической ёмкостной самоиндукции поскольку наличие тока связано с изменением такого параметра как ёмкость. Рассмотрим следствия, вытекающие из соотношения (4.1.2).
Если к емкости подключить генератор постоянного тока ![]() , то напряжение на ней будет изменяться по закону:
, то напряжение на ней будет изменяться по закону:
(4.1.4)
Таким образом, емкость, подключенная к источнику постоянного тока, представляет для него активное сопротивление
(4.1.5)
которое линейно зависит от времени. Следует отметить, что полученный результат является вполне очевидным, однако такие свойства ёмкости, которую принято считать реактивным элементом впервые были отмечены в работе [4].
С физической точки зрения это понятно, т.к., чтобы заряжать емкость, источник должен расходовать энергию.
Мощность, отдаваемая источником тока, определяется в данном случае соотношением:
(4.1.6)
Энергию, накопленную емкостью за время ![]() , получим, проинтегрировав соотношение (4.1.6) по времени:
, получим, проинтегрировав соотношение (4.1.6) по времени:
Подставляя сюда значение тока из соотношения (4.1.4), получаем зависимость величины накопленной в емкости энергии от текущего значения напряжения на ней:
Используя для рассмотренного случая понятие потока электрической индукции
(4.1.7)
и используя соотношение (4.1.2), получаем:
(4.1.8)
т.е., если к постоянной емкости подключить источник постоянного тока, то величина тока будет равна производной потока ёмкостной индукции по времени.
Теперь будем поддерживать на емкости постоянное напряжение ![]() , а изменять саму ёмкость, тогда
, а изменять саму ёмкость, тогда
(4.1.9)
Видно, что величина
(4.1.10)
играет роль активного сопротивления. Этот результат тоже физически понятен, т.к. при увеличении емкости увеличивается накопленная в ней энергия, и таким образом, ёмкость отбирает у источника напряжения энергию, представляя для него активную нагрузку. Мощность, расходуемая при этом источником, определяется соотношением:
(4.1.11)
Из соотношения (4.1.11) видно, что в зависимости от знака производной расходуемая мощность может иметь разные знаки. Когда производная положительная, расходуемая мощность идёт на совершение внешней работы. Если производная отрицательная, то работу совершает внешний источник. Опять, вводя понятие поток ёмкостной индукции
получаем
(4.1.12)
Соотношения (4.1.8) и (4.1.12) указывают на то, что независимо от того, каким способом изменяется поток, его производная по времени всегда равна току. Рассмотрим еще один процесс, который ранее к законам индукции не относили, однако, он подпадает под наше расширенное определение этого понятия. Из соотношения (4.1.7) видно, что если поток, т.е. заряд, оставить неизменным (будем называть этот режим режимом замороженного ёмкостного потока), то напряжение на емкости можно изменять путем ее изменения. В этом случае будет выполняться соотношение:
где ![]() и
и ![]() - текущие значения, а
- текущие значения, а ![]() и
и ![]() - начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
Напряжение на емкости и энергия, накопленная в ней, будут при этом определяться соотношениями:
- начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
Напряжение на емкости и энергия, накопленная в ней, будут при этом определяться соотношениями:
(4.1.13)
Естественно, что данный процесс самоиндукции может быть связан только с изменением самой емкости, и поэтому он подпадает под определение параметрической самоиндукции.
Таким образом, имеются три соотношения (4.1.8), (4.1.12) и (4.1.13), которые определяют процессы ёмкостной самоиндукции. Будем называть их правилами ёмкостного потока. Соотношение (4.1.8) определяет ёмкостную самоиндукцию, при которой отсутствуют изменения емкости, и поэтому эта самоиндукция может быть названа просто ёмкостной самоиндукцией. Соотношения (4.1.3) и (4.1.9–4.1.11) предполагают наличие изменений емкости, поэтому процессы, соответствующие этими соотношениями, будем называть ёмкостной параметрической самоиндукцией.
Индуктивная самоиндукция
Перейдем теперь к рассмотрению процессов, происходящих в индуктивности. Введем понятие потока индуктивной самоиндукции
Если индуктивность закорочена, и выполнена из материала, не имеющего активного сопротивления, например из сверхпроводника, то
где ![]() и
и ![]() - какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
- какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
Этот режим будем называть режимом замороженного тока. При этом выполняется соотношение:
(4.2.1)
где ![]() и
и ![]() - текущие значения соответствующих параметров.
- текущие значения соответствующих параметров.
В рассмотренном режиме поток индукции остается неизменным, однако, в связи с тем, что ток в индуктивности может изменяться при ее изменении, такой процесс подпадает под определение параметрической самоиндукции. Энергия, накопленная в индуктивности, при этом будет определяться соотношением
Напряжение на индуктивности, равно производной потока индуктивной индукции по времени:
Рассмотрим случай, когда индуктивность ![]() постоянна, тогда
постоянна, тогда
(4.2.2)
Проинтегрировав выражение (4.2.2) по времени, получим:
(4.2.3)
Таким образом, индуктивность, подключенная к источнику постоянного напряжения, представляет для него активное сопротивление
(4.2.4)
которое уменьшается обратно пропорционально времени.
Мощность, расходуемая при этом источником, определится соотношением:
(4.2.5)
Эта мощность линейно зависит от времени. Проинтегрировав соотношение (4.2.5) по времени, получим энергию, накопленную в индуктивности
(4.2.6)
Подставив в выражение (4.2.6) значение напряжения из соотношения (4.2.3), получаем:
Эта энергия может быть возвращена из индуктивности во внешнюю цепь, если индуктивность отключить от источника питания и подключить к ней активное сопротивление.
Теперь рассмотрим случай, когда ток ![]() , протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
, протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
(4.2.7)
Таким образом, величина
(4.2.8)
играет роль активного сопротивления.
Как и в случае электрического потока, активное сопротивление может быть (в зависимости от знака производной), как положительным, так и отрицательным. Это означает, что индуктивность может, как получать энергию извне, так и отдавать её.
Вводя обозначение ![]() и, учитывая (4.2.7), получаем:
и, учитывая (4.2.7), получаем:
(4.2.9)
Соотношения (4.2.1), (4.2.6) и (4.2.9) будем называть правилами индуктивной самоиндукции, или правилами потока индуктивной самоиндукции. Из соотношений (4.2.6) и (4.2.9) видно, что, как и в случае с ёмкостным потоком, способ изменения индуктивного потока не влияет на конечный результат, и его производная по времени всегда равна приложенной разности потенциалов. Соотношение (4.2.6) определяет индуктивную самоиндукцию, при которой отсутствуют изменения индуктивности, и поэтому она может быть названа просто индуктивной самоиндукцией. Соотношения (4.2.7,4.2.8) предполагают наличие изменений индуктивности, поэтому процессы, описываемые этими соотношениями, будем называть индуктивной параметрической самоиндукцией.
Новый способ получения волнового уравнения
Процессы, рассмотренные в двух предыдущих параграфах, касаются цепей с сосредоточенными параметрами, когда распределение разностей потенциалов и токов в рассмотренных элементах можно считать однородным. Однако имеются цепи, например длинные линии, в которых разности потенциалов и токи не являются пространственно однородными. Эти процессы описываются волновыми уравнениями, которые могут быть получены из уравнений Максвелла или при помощи телеграфных уравнений, но физика самого явления нам не ясна.
Воспользуемся результатами, полученными в предыдущем параграфе для рассмотрения процессов, происходящих в длинных линиях, в которых емкость и индуктивность являются распределенными параметрами. Предположим, что погонная (приходящаяся на единицу длины) емкость и индуктивность такой линии составляют соответственно ![]() и
и ![]() . Если к такой линии подключить источник постоянного напряжения
. Если к такой линии подключить источник постоянного напряжения ![]() , то его фронт будет распространяться в линии с какой-то скоростью
, то его фронт будет распространяться в линии с какой-то скоростью ![]() , и текущая координата этого фронта определится соотношением
, и текущая координата этого фронта определится соотношением ![]() . При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
. При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
Источник напряжения ![]() будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением (4.1.9) должен течь ток:
будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением (4.1.9) должен течь ток:
(5.1)
Этот ток будет протекать через проводники линии, обладающие индуктивностью. Но, поскольку индуктивность линии в связи с движением фронта напряжения, тоже увеличивается, то в соответствии с соотношением (4.2.7), на ней будет наблюдаться падение напряжения:
Но падение напряжения на проводниках линии по абсолютной величине равно напряжению, приложенному к её входу, поэтому в последнем выражении следует допустить, что ![]() . С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения
. С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения ![]() должна составлять
должна составлять
(5.2)
Это выражение соответствует скорости распространения электромагнитных колебаний в самой линии. Следовательно, если к бесконечно длинной линии подключить источник напряжения, то в ней будет иметь место саморасширение и ёмкостного и индуктивного потоков, заполняющих линию энергией, и скорость фронта постоянного напряжения и тока будет равна скорости распространения электромагнитных колебаний в такой линии. Такую волну будем называть электротоковой. Интересно отметить, что полученный результат не зависит от вида функции ![]() , т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (5.2) . Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью
, т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (5.2) . Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью ![]() , оставляет за собой линию, заряженную до разности потенциалов
, оставляет за собой линию, заряженную до разности потенциалов ![]() , что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток
, что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток ![]() , что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
, что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
Величину тока в линии можно получить, подставив значения скорости распространения фронта волны, определяемого соотношением (5.2), в соотношение (5.1). Сделав эту подстановку, получим
где  - волновое сопротивление линии.
- волновое сопротивление линии.
В данном случае
Так точно
Видно, что правила потока и для индуктивной и для ёмкостной самоиндукции соблюдаются и в этом случае.
Таким образом, процессы распространения разности потенциалов вдоль проводников длинной линии и постоянного тока в ней являются связанными и взаимно дополняющими друг друга, и существовать друг без друга не могут. Такой процесс можно называть ёмкостно-индуктивной самопроизвольной параметрической самоиндукцией. Такое название связано с тем, что расширение потоков происходят самопроизвольно и характеризуют скорость процесса заполнения линии энергией. Из выше изложенного становится понятной связь между энергетическими процессами и скоростью распространения фронтов волны в длинных линиях. Поскольку при излучении электромагнитных волн свободное пространство тоже является передающей линией, то подобные законы должны характеризовать и распространение в таком пространстве.
Что будет, например, в том случае, если в качестве одного из проводников длинной линии взять спираль, или как это принято называть, длинный соленоид. Очевидно, в этом случае скорость распространения фронта напряжения в такой линии уменьшится, поскольку погонная индуктивность линии увеличится. При этом такому распространению будет сопутствовать процесс распространения не только внешних, по отношению к соленоиду полей и токов, но и процесс распространения магнитного потока внутри самого соленоида и скорость распространения такого потока будет равна скорости распространения электромагнитной волны в самой линии.
Зная ток и напряжение в линии, можно вычислить удельную энергию, заключенную в погонной ёмкости и индуктивности линии. Эти энергии будут определяться соотношениями:
(5.3)
(5.4)
Теперь обсудим вопрос о длительности фронта электротоковой волны и о том, какое пространство этот фронт будет занимать в самой линии. Ответ на первый вопрос определяется свойствами самого источника напряжения, т.к. локальная производная ![]() на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время
на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время ![]() , то в линии он займет участок длиной
, то в линии он займет участок длиной ![]() . Если к линии приложить напряжение, меняющееся со временем по закону
. Если к линии приложить напряжение, меняющееся со временем по закону ![]() , то это же значение функции будет наблюдаться в любой точке линии на расстоянии
, то это же значение функции будет наблюдаться в любой точке линии на расстоянии ![]() от ее начала с запаздыванием
от ее начала с запаздыванием ![]() . Таким образом, функция
. Таким образом, функция
(5.5)
может быть названа функцией распространения, т.к. она устанавливает связь между локальными временными и пространственными значениями функции в линии. Длинная линия является устройством, которое локальные производные напряжения по времени на входе линии превращает в пространственные производные в самой линии. На основании функции распространения (5.5) можно установить связь между локальными и пространственными производными в длинной линии. Очевидно, что
Важно отметить, что сам процесс распространения в данном случае обязан естественному саморасширению электрического поля и тока в линии, и он подчиняется правилам параметрической самоиндукции. Во-вторых, для решения волновых уравнений длинных линий
(5.6)
полученных из телеграфных уравнений
требуется знание вторых производных напряжений и токов. Но как быть, если на вход линии подаётся напряжение, у которого вторая производная равна нулю (случай, когда напряжение источника меняется по линейному закону)? Ответа на этот вопрос уравнения (5.6) не дают. Используемый метод даёт ответ на такой вопрос.
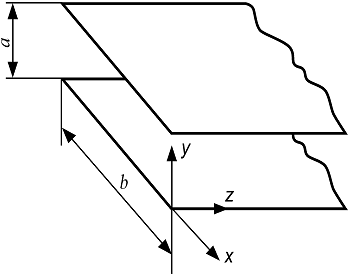
При рассмотрении процессов в длинной линии фигурировали такие понятия как погонная емкость и индуктивность, а также токи и напряжения в линии. Однако в электродинамике, основанной на уравнениях Максвелла, нет таких понятий как емкость и индуктивность, а есть понятия электрической и магнитной проницаемости среды. В проведенном рассмотрении также отсутствовали такие понятия как электрические и магнитные поля. Покажем, как перейти от таких категорий как «погонная индуктивность и ёмкость», и «ток» и «напряжение» в линии к таким понятиям как «диэлектрическая и магнитная проницаемость», а также «электрическое и магнитное поле». Для этого возьмем простейшую конструкцию линии, расположенную в вакууме, как показано на рис. 4.
Рис. 4 Двухпроводная линия, состоящая из двух идеально проводящих плоскостей
Будем считать, что ![]() >>
>> ![]() и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
(5.7)
(5.8)
где ![]() и
и ![]() - магнитная и диэлектрическая проницаемость вакуума.
- магнитная и диэлектрическая проницаемость вакуума.
Фазовая скорость в такой линии будет определяться соотношением:
где ![]() - скорость распространения света в вакууме.
- скорость распространения света в вакууме.
Волновое сопротивление рассмотренной линии будет равно:
где 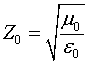 - волновое сопротивление свободного пространства.
- волновое сопротивление свободного пространства.
Кроме этого при соблюдении условия ![]() получаем равенство
получаем равенство ![]() . Это означает, что магнитная проницаемость
. Это означает, что магнитная проницаемость ![]() играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство
играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство ![]() . Это означает, что диэлектрическая проницаемость
. Это означает, что диэлектрическая проницаемость ![]() играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и
играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и ![]() , и
, и ![]() приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
Рассмотрение электромагнитной волны в длинной линии можно рассматривать как заполнение пространства, находящегося между её проводниками, особым видом материи, которую представляют электрические и магнитные поля. Математически можно считать, что эти поля сами обладают удельной энергией и при их помощи можно передавать энергию по линиям передач. Если же рассматривать процессы, протекающие при излучении электромагнитных волн при помощи какой-либо антенны, то его можно рассматривать также как заполнение свободного пространства этим видом материи. Однако геометрический вид полей и токов в этом случае будет сложнее, поскольку всегда будут присутствовать как поперечные, так и продольные составляющие полей. Такой подход исключает необходимость применения, для описания распространения электромагнитных волн, такой субстанции как эфир.
Если к рассмотренной линии бесконечной длины, или линии нагруженной волновым сопротивлением, подключить источник постоянного напряжения ![]() , то напряженность поля в линии составит:
, то напряженность поля в линии составит:
а ток, текущий в линию от источника питания, будет определяться соотношением:
(5.9)
Магнитное поле в линии будет равно удельному току, протекающему в линии
Подставляя сюда значение ![]() , получаем
, получаем
(5.10)
Такая же связь между электрическим и магнитным полем существует и для случая поперечных электромагнитных волн, распространяющихся в свободном пространстве.
Сравнивая выражения для энергий, нетрудно видеть, что удельные энергии могут быть выражены через электрические и магнитные поля
(5.11)
Это означает, что удельная энергия, накопленная в магнитном и электрическом поле в такой линии одинакова. Если значения этих энергий умножить на объемы, занимаемые полями, то полученные величины совпадают с выражениями (5.3,5.4).
Таким образом, приходим к выводу, что в рассмотренной линии распространяются такие же поперечные плоские волны, как и в свободном пространстве. Причем этот вывод получен не путём решения уравнений Максвелла, а путём рассмотрения динамических процессов, которые отнесены к разряду параметрической самоиндукции. Особенностью такой линии будет то, что в ней, в отличие от свободного пространства, могут распространяться постоянные магнитные и электрические поля, а этот случай не может быть рассмотрен путем решения уравнений Максвелла.
Следовательно, условно можно считать, что длинная линия является устройством, которое при подключении к ней источника постоянного напряжения заполняется двумя видами энергии: электрической и магнитной. Удельные плотности этих энергий равны, а поскольку и электрическая и магнитная энергии заполняют одинаковые объемы, то и общая энергия, накопленная в этих полях одинакова. Особенностью данной линии является то, что при протекании в линии постоянного тока распределение электрического и магнитного полей в ней является однородным. Нетрудно показать, что сила, действующая на проводники такой линии, равна нулю. Это следует из соотношения (5.11), в котором его правая и левая части представляют удельные силы, приложенные к плоскостям линии. Но электрическая и магнитная силы имеют разные знаки, поэтому они компенсируют друг друга. Этот вывод касается и передающих линий любой другой конфигурации.
Если к линии приложить напряжение, меняющееся со временем по любому закону![]() , то по аналогии с (5.5) можно записать
, то по аналогии с (5.5) можно записать
(5.12)
Аналогичное соотношение будет и для магнитных полей.
Очевидно, что произведение ![]() представляет мощность
представляет мощность ![]() , передаваемую через поперечное сечение линии в направлении
, передаваемую через поперечное сечение линии в направлении ![]() . Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим
. Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим ![]() . Произведение
. Произведение ![]() представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
Таким образом, все выводы, полученные на основании рассмотрения процессов в длинной линии двумя методами, совпадают. Поэтому и в дальнейшем, не рискуя допустить ошибки принципиального характера, можно для описания процессов в длинных линиях с успехом пользоваться такими параметрами, как распределенная индуктивность и ёмкость. Конечно, при этом следует понимать, что ![]() и
и ![]() это некоторые интегральные характеристики, не учитывающие структуру полей. Следует отметить, что с практической точки зрения, применение параметров
это некоторые интегральные характеристики, не учитывающие структуру полей. Следует отметить, что с практической точки зрения, применение параметров ![]() и
и ![]() имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.
имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.
Переходные процессы в отрезках длинных линий
Фарадей установил закон индукции, проводя эксперименты на соленоидах, включая и выключая в них ток, или двигая по отношению к соленоидам, через которые протекал постоянный ток, витки проволоки, к которым подключался гальванометр. Его точка зрения, которая считается верной и сегодня, сводилась к тому, что если к соленоиду подключён источник постоянного напряжения ![]() , то ток во всех его витках нарастает по линейному закону
, то ток во всех его витках нарастает по линейному закону
(6.1)
где ![]() - индуктивность соленоида.
- индуктивность соленоида.
Следовательно, магнитное поле при такой интерпретации на всём протяжении соленоида будет нарастать синхронно. Однако так ли это на самом деле? Для того чтобы разобраться в этом, рассмотрим вопрос о том, как будет нарастать ток в закороченном отрезке длинной линии.
Если линию (рис. 4) закоротить на расстоянии ![]() от ее начала, то суммарная индуктивность линии составит величину
от ее начала, то суммарная индуктивность линии составит величину 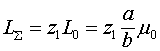 . Если подключить к линии источник постоянного напряжения, в ней начнет распространяться волна тока
. Если подключить к линии источник постоянного напряжения, в ней начнет распространяться волна тока 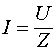 и напряжения
и напряжения ![]() , как показано на рис. 5 .
, как показано на рис. 5 .
Волна тока в правой своей части имеет переходной участок ![]() , который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса
, который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса 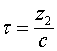 , за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
, за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
Рис. 5. Распространение волны тока и напряжения в длинной линии.
Именно на этом переходном участке и происходит ускорение зарядов от нулевой скорости в его начале, до значений необходимых для создания номинального тока в линии, величина которого определяется соотношением 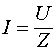 . К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Принято также, что время этого переходного процесса значительно меньше, чем время, за которое фронт напряжения пробегает по линии в одну сторону. Интервал
. К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Принято также, что время этого переходного процесса значительно меньше, чем время, за которое фронт напряжения пробегает по линии в одну сторону. Интервал ![]() соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что
соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что ![]() >>
>>![]() .
.
В момент, когда на перемычке, закорачивающей длинную линию, на которой выполняется граничное условие ![]() , появляется фронт напряжения
, появляется фронт напряжения ![]() , возникает отраженная волна с напряжением
, возникает отраженная волна с напряжением ![]() , бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен
, бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен  , т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный
, т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный ![]() , и нулевое напряжение. Когда фронт напряжения возвратиться к началу линии, он принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию фронт напряжения
, и нулевое напряжение. Когда фронт напряжения возвратиться к началу линии, он принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию фронт напряжения ![]() и ток
и ток ![]() . Этот ток сложится с током
. Этот ток сложится с током ![]() , и суммарный ток в линии составит
, и суммарный ток в линии составит ![]() . Ток и далее будет нарастать ступеньками, добавляя каждый очередной раз к своему прежнему значению величину
. Ток и далее будет нарастать ступеньками, добавляя каждый очередной раз к своему прежнему значению величину ![]() . Если этот процесс отобразить во времени, то он будет выглядеть, как показано на рис. 6.
. Если этот процесс отобразить во времени, то он будет выглядеть, как показано на рис. 6.
На этом рисунке время
равно времени, за которое фронт напряжения пробегает по линии в одну сторону от её начала до закороченного участка.
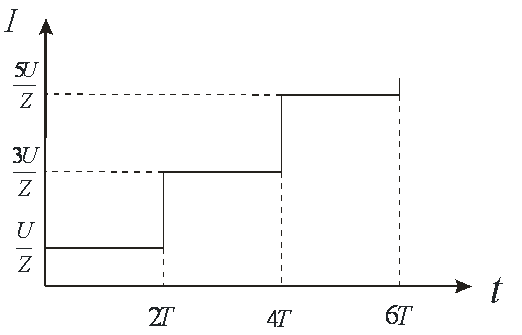
Особенностью такого процесса является то, что отбор энергии от источника напряжения не будет подчиняться линейному закону, а будет иметь скачкообразный характер. Мощность, отбираемая на интервале времени от нуля до ![]() , будет составлять
, будет составлять ![]() . Но на каждом последующем интервале времени, равном
. Но на каждом последующем интервале времени, равном ![]() , она будет возрастать уже на величину
, она будет возрастать уже на величину ![]() .
.
Рис. 6. График зависимости входного тока от времени для закороченной линии.
Таким образом, нарастание тока носит вовсе не линейный, а скачкообразный характер, и он тем более выражен, чем больше длина линии. Указанный процесс имеет место при любой длине линии. При малой длине линии скачки следуют через малые промежутки времени и зависимость тока от времени приближенно можно считать линейной, что и характерно для элементов с сосредоточенными параметрами.
Следует обратить внимание на то, что, мощность, отбираемая закороченной линией у источника напряжения (рис. 6), не является линейной функцией, а по истечении времени равному ![]() скачком увеличивается на
скачком увеличивается на ![]() , причем первый скачек соответствует отбираемой мощности
, причем первый скачек соответствует отбираемой мощности ![]() . Нетрудно показать, что магнитный поток в данном случае изменяется по линейному закону (рис. 7). Действительно, во время прямого хода, до момента достижения волной закороченного участка, поток будет увеличиваться по линейному закону, и к моменту
. Нетрудно показать, что магнитный поток в данном случае изменяется по линейному закону (рис. 7). Действительно, во время прямого хода, до момента достижения волной закороченного участка, поток будет увеличиваться по линейному закону, и к моменту ![]() достигнет величины
достигнет величины  . Когда, отразившись от закороченного участка, фронт напряжения начнет двигаться в обратном направлении, то поток будет продолжать возрастать по линейному закону, и к моменту прихода фронта напряжения обратно к источнику напряжения достигнет величины
. Когда, отразившись от закороченного участка, фронт напряжения начнет двигаться в обратном направлении, то поток будет продолжать возрастать по линейному закону, и к моменту прихода фронта напряжения обратно к источнику напряжения достигнет величины  Таким образом, при подключении закороченной линии к источнику напряжения выполняется закон индукции.
Таким образом, при подключении закороченной линии к источнику напряжения выполняется закон индукции.  .
.
Рис. 7. Зависимость магнитного потока от времени для закороченной линии.
Электрический поток в линии тоже будет изменяться, но по другому закону (рис. 8).
Рис. 8. Зависимость электрического потока от времени для закороченной линии.
В отличие от магнитного потока он будет изменяться периодически, то, возрастая, то, убывая, по линейному закону. Когда волна движется в положительном направлении, одновременно возрастает и магнитный и электрический поток. При этом, как в магнитном, так и в электрическом поле накопленная энергия возрастает. Когда волна начинает двигаться в обратном направлении, то электрическое поле начинает исчезать, а его энергия переходит в магнитную энергию обратной волны тока. После того, как фронт волны напряжения достигает входа линии, магнитное поле и ток в ней удваивается, а электрическое поле исчезает. Далее цикл повторяется. Следовательно, процессу возрастания магнитного потока в индуктивности закороченной длинной линия, в обязательном порядке сопутствует процесс периодического изменения потока электрической индукции, в результате чего между плоскостями линии периодически возникает и исчезает электрическое поле.
Допустим, что линия выполнена из сверхпроводника и не имеет потерь. Тогда заменив в определённый момент генератор напряжения сверхпроводящей перемычкой, можно заморозить ток в линии. Наиболее благоприятным моментом для такой процедуры является момент, когда в линии полностью отсутствует электрическое поле. Тогда в линии будет заморожен поток 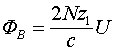 , которому будет соответствовать ток
, которому будет соответствовать ток  . Что будет, если замену источника напряжения сверхпроводящей перемычкой произвести в тот момент времени, когда в линии находится фронт напряжения и какой-то её участок заполнен электрическими полями? В этом случае этот участок будет двигаться в линии, попеременно отражаясь то от одного, то от другого конца закороченной линии, пока не истратит свою энергию на излучение. По этой причине в закороченной с обеих сторон линии может быть заморожено только целочисленное (квантованное) значение потока и тока в соответствии с приведенными соотношениями.
. Что будет, если замену источника напряжения сверхпроводящей перемычкой произвести в тот момент времени, когда в линии находится фронт напряжения и какой-то её участок заполнен электрическими полями? В этом случае этот участок будет двигаться в линии, попеременно отражаясь то от одного, то от другого конца закороченной линии, пока не истратит свою энергию на излучение. По этой причине в закороченной с обеих сторон линии может быть заморожено только целочисленное (квантованное) значение потока и тока в соответствии с приведенными соотношениями.
Это явление является примером макроскопического квантования потока в макроскопических структурах, имеющих определённые размеры. Такое же квантование потока происходит и в микроскопических структурах, которыми являются атомы.
С точки зрения цепей с сосредоточенными параметрами, нарастание тока в соленоиде при подключении к нему источника напряжения происходит по линейному закону, причём во всех его витках одновременно. Но так ли это? Для выяснения этого вопроса заменим верхнюю плоскость рассмотренной двухпроводной линии (рис. 9) длинным соленоидом. Если к такой линии подключить источник напряжения, то процесс нарастания тока в ней ничем не будет отличаться от рассмотренного. Погонная индуктивность линии будет теперь в основном определяться погонной индуктивностью соленоида и скорость распространения и волны тока, и волны напряжения (напряжение теперь будет приложено между соленоидом и нижним проводником линии) будет меньше, чем в предыдущем случае.
Когда в рассмотренной линии волна дойдет до точки с координатой ![]() , то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой
, то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой ![]() . Когда волна дойдет до его конца, то магнитным полем будет заполнен весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, внутренний магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида.
. Когда волна дойдет до его конца, то магнитным полем будет заполнен весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, внутренний магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида.
Рис. 9. Схема распространения магнитных полей в длинном соленоиде.
Положим теперь, что соленоид в определенном месте охвачен витком.
Этот процесс подобен механическому одеванию охватывающего витка на конец соленоида с той лишь разницей, что в данном случае магнитный поток, перемещаясь внутри соленоида, сам пронизывает охватывающий его виток. Причём скорость движения фронта магнитного потока при этом несоизмеримо больше, чем при механическом одевании. Но оба процесса имеют одинаковую природу. Этими процессами и объясняется явление взаимной индукции между соленоидом и охватывающим витком. При небольшой длине соленоида расстояние между импульсами невелико, поэтому они сливаясь, образуют почти постоянное напряжение. Напряжение в витке будет индуцироваться только в момент пересечения магнитным потоком соленоида окрестностей поперечного сечения, охваченного витком. В этот момент в окрестностях охватывающего витка будет возникать, как векторный потенциал, так и магнитное поле. И, именно, пересечение охватывающего витка магнитными полями рассеяния (такого же, как и на конце соленоида с постоянным током) приводит к индуцированию в нём э.д.с. Этот момент будет наступать как при прямом, так и при обратном ходе волны, причем полярность импульсов напряжения, индуцируемых в витке, в обоих случаях будет одна и та же. Частота этих импульсов будет зависеть от длины соленоида, и будет тем больше, чем короче соленоид. Следовательно, среднее значение индуцированного напряжения будет расти с уменьшением длины соленоида, т.е. его количества витков, что и определяет коэффициент трансформации такого трансформатора, который равен отношению количества витков соленоида и охватывающей обмотки.
Во времена Фарадея не было известно, каким образом распространяются поля в длинных линиях, поэтому учесть эти особенности при написании своего закона он не мог. Но во времена Аронова, Бома и Фейнмана всё это было хорошо известно, поэтому вызывает недоумение тот факт, что этот процесс в их бытность не был описан правильно.
Список литературы
- 1. Левич В. Г. Курс теоретической физики, том 1. Теория электромагнитного поля, теория относительности, статистическая физика, М: Физматгиз, 1962, 695 –с.
- 2. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 3. Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. М: Физматгиз, 1973.- 454 с.
- 4. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 5. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. ч. 6 Электродинамика. М: Мир, 1977.
- 6. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 7. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с. ISBN – 966-7983-55-2.