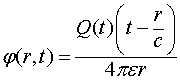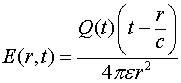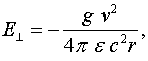Эксперименты, опровергающие специальную теорию относительности
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
Успехи специальной теории относительности (СТО) связаны с тем, что в отдельных случаях она правильно предсказывает некоторые электродинамические явления, например фазовую аберрацию и поперечный эффект Доплера. Однако некоторые её следствия физически неприемлемы. Физически абсурдными являются предсказания того, что при своём движении материальные тела при достижении скорости света сжимаются до нулевых размеров в направлении движения. То же касается и эффекта близнецов, когда человек, летающий в космическом корабле со световой скоростью, может жить бесконечно долго. Такие недопустимые с физической точки зрения результаты СТО явились следствием того, что с момента её создания в 1905 году, физика пошла по пути математической схоластизации физических процессов, ничего общего с физикой не имеющих. При этом математика начала изобретать свои собственные «физические» законы, которых в природе нет. Одним из таких законов и является СТО.
Приверженцы СТО заявляют, что нет таких физических экспериментов, которые противоречили бы этой теории. Именно о двух таких экспериментах и пойдёт речь в данной статье.
Электрический импульс ядерного взрыва
США по программе «Starfish» 9 июля 1962 взорвали в космосе над Тихим океаном водородную бомбу с тротиловым эквивалентом 1.4 Мт. Это событие поставило перед научной общественностью очень много вопросов. Перед этим в 1957 г. будущий нобелевский лауреат доктор Ханс Альбрехт Бете (Hans A. Bethe), основываясь на теории дипольного излучения, предсказал, что при подобном взрыве будет наблюдаться электромагнитный импульс (ЭМИ) при этом напряженность поля на поверхности земли составит не более 100 В/м. Но при взрыве бомбы произошло неожиданное. Напряженность электрических полей, начиная с эпицентра взрыва, и далее на протяжении более 1000 км достигла нескольких десятков тысяч вольт на метр. (Карта местности и значения напряженностей полей приведены на рис. 1.) Очень похожие результаты были получены и при подобных испытаниях в СССР по программе «Программа К». Рисунок 1 и все данные, которые будут приведены в этом разделе, касающиеся испытаний по программам «Starfish» и «Программа К», взяты с сайта http://glasstone.blogspot.com/2006/03/emp-radiation-from-nuclear-space.html.
К сожалению, в материалах данной ссылки не содержится информация о поляризации этих полей. Возможность уточнить этот вопрос дают данные, полученные во время испытаний с кодовым названием «Программа К», когда недалеко от Джезказгана на высоте 290 км была взорвана водородная бомба с тротиловым эквивалентом 300 кт. Карта местности с указанием значений напряженностей полей, полученных при этом взрыве, показана на рис. 2.
Сравнивая данные по напряженностям полей, приведенные на этих двух картах, можно видеть, что значения напряженностей полей на рис. 1 убывают при увеличении расстояния от эпицентра взрыва, в то время как на карте, изображенной на рис. 2, эти значения возрастают. Из этого можно сделать вывод, что на второй карте приведены данные по измерению горизонтальной составляющей напряженностей электрических полей, поскольку в первом случае измерялась вертикальная составляющая электрического поля импульса.
Рис. 1. Карта испытаний по программе «Starfish».
Рис. 2. Карта испытаний по программе «Программа К».
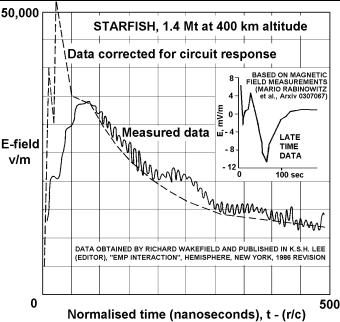
Имеется запись формы электрического импульса, сделанная на расстоянии 1300 км от места взрыва (рис. 3), полученная при испытаниях по программе «Starfish». Из приведенного рисунка видно, что ЭМИ имеет не только очень большую амплитуду, но и очень малую длительность.
Поскольку прогноз доктора Ханса Альбрехта Бете не оправдался, то в последующем было выдвинуто еще две теории, призванные объяснить экспериментальные данные. Первая из них была разработана доктором Конрадом Лонгмаером (Conrad Longmire) в 1963 г, который рассмотрел вопрос о формировании магнитного диполя, образуемого комптоновскими электронами, вращающимися вокруг силовых линий магнитного поля Земли.
В последующем в 1975 г. была разработана модель Louis W. Seiler, Jr report AD-A009208, March 1975 http://glasstone.blogspot.com/2006/03/emp-radiation-from-nuclear-space.html , в которой предполагается, что формирование ЭМИ обязано релятивистским комптоновским электронам, которые выбивает из молекул воздуха жесткое рентгеновское излучение и которые синфазно с гамма-излучением двигаются с релятивистскими скоростями в направлении распространения электромагнитной волны. Ни та, ни другая модель достоверно принята или опровергнута быть не может, поскольку дальнейшие испытания ядерного оружия в космосе были прекращены, и нет дополнительных экспериментальных данных, которые смогли бы подтвердить или опровергнуть рассмотренные модели.
Рис. 3. Экспериментальная зависимость амплитуды ЭМИ от времени, полученная при испытаниях по программе «Starfish».
Эти модели предполагают, что процесс формирования ЭМИ не является свойством самого взрыва, а является вторичным эффектом, связанным с тем, что рентгеновское излучения выбивает из молекул воздуха комптоновские электроны. Из последней модели, получившей наибольшее признание, вытекает, что сам ЭМИ распространяется из ионосферы в нижние слои атмосферы, и, следовательно, его поля выше ионосферы, непосредственно в самом космосе, отсутствуют. Но, если при помощи рассмотренных теорий еще как-то можно объяснить наличие электрических полей в зоне видимости взрыва, то факт сильных возмущений ионосферы на больших расстояниях от взрыва, которые ему сопутствовали, объяснить трудно. Так, после взрыва по программе «Starfish» в течении нескольких десятков минут отсутствовала радиосвязь с Японией и Австралией, и даже на расстоянии в 3200 км от эпицентра взрыва были зафиксированы возмущения ионосферы, которые в несколько раз превышали те, которые бывают обусловлены самыми мощными вспышками на Солнце. Взрыв повлиял и на космические аппараты. Три спутника были сразу выведены из строя электромагнитным импульсом. Заряженные частицы, появившиеся в результате взрыва, были захвачены магнитосферой Земли, в результате чего их концентрация в искусственном радиационном поясе Земли увеличилась на 2-3 порядка. Воздействие радиационного пояса привело к очень быстрой деградации солнечных батарей и электроники еще у семи спутников, в том числе и у первого коммерческого телекоммуникационного спутника Телестар 1. В общей сложности взрыв вывел из строя треть космических аппаратов, находившихся на низких орбитах в момент взрыва.
При взрыве ядерного заряда по программе «Программа К» радиосвязь и радарные установки были также блокированы на расстоянии до 1000 км. В результате этих испытаний было установлено, что высотные ядерные взрывы сопровождаются излучением электромагнитного импульса (ЭМИ) в широком диапазоне частот, значительно превышающего по амплитуде величину ЭМИ, излучаемого при приземных взрывах той же мощности. Было обнаружено, что регистрация ЭМИ высотного ЯВ возможна на больших (до 10 тысяч километров) расстояниях от места взрыва. http://atomas.ru/isp2/1_9.htm.
С точки зрения существующих понятий классической электродинамики комптоновские модели вызывают серьезные вопросы. Например, почему все комптоновские электроны должны двигаться синфазно с фронтом гамма-излучения с релятивистской скоростью. У комптоновских электронов вектор скорости имеет пространственное распределение, в связи с чем нельзя получить такой короткий фронта нарастания импульса, как это имеет место в действительности. В линейной электродинамике теоретически отсутствуют такие механизмы, которые дают возможность получить в данном месте однополярный импульс электрического поля без пространственного разделения зарядов. Но за время нарастания импульса, которое исчисляется десятками наносекунд, получить пространственное разделение зарядов, которое обеспечит полученную на эксперименте напряженность поля, невозможно. Сама же комптоновская ионизация оставляет всю систему в целом электронейтральной.
Известно, что проблему ЭМИ вместе со своими учениками пытался решить и Академик АН СССР Я. Б. Зельдович [1]. Однако в имеющихся источниках по этому вопросу нет информации о том, что им эта проблема была решена. Следовательно, все говорит о том, что в рамках существующей классической электродинамики результаты, полученные при испытаниях по программе «Starfish» и «Программа К», объяснить пока нельзя. Не даёт ответ на поставленный вопрос и СТО.
В чем заключается опасность прогнозов, которые дает последняя модель? Проблема в том, что эта модель исключает возможность наличия полей ЭМИ в самом космосе. Предположим, что модель выдвинутая Louis W. Seiler, Jr. неверна, и, опираясь на неё, как в прошлом на передсказания доктора Ханса Альбрехта Бете, будет произведен очередной взрыв ядерного заряда в космосе, который выведет из строя большое количество спутников. Причём этот взрыв может быть как запланированным, так и осуществлённым в террористических целях. Тогда уже оправдываться будет поздно.
Предпримем попытку, используя концепцию скалярно-векторного потенциала, объяснить полученные экспериментальные данные, а также покажем, что при взрыве ядерного заряда в космосе, там существуют не электромагнитные поля, а импульсные электрические поля (ИЭП), в которых магнитное поле отсутствует [2-4]. Причем поля ИЭП в космосе имеют гораздо более значительные величины, чем в атмосфере и на земной поверхности.
В начальный момент термоядерного взрыва температура сгустка плазмы может достигать нескольких сот миллионов градусов. При таких температурах электронный газ уже не является вырожденным и подчиняется распределению Больцмана. Предположим, что температура образовавшегося при взрыве плазменного сгустка в начальный момент составляет ~ 108 К, а общий вес бомбы, выполненной из металла со средней плотностью электронов ~5× 1022 1/см3, составляет 1000 кг. При удельном весе металла ~ 8 г/ см3 общее количество свободных электронов в образовавшейся плазме, в предположении, что все атомы будут однократно ионизированы, составит ~ 5×1027. Наиболее вероятную скорость электронов при указанной температуре определим из соотношения:
где ![]() - постоянная Больцмана, а
- постоянная Больцмана, а ![]() - масса электрона.
- масса электрона.
При таких скоростях приращение скалярно-векторнго потенциала при учёте только члены разложения ~ ![]() , составит [3,4]
, составит [3,4]
(1.1)
где ![]() - свободных электронов,
- свободных электронов, ![]() - заряд электрона, а
- заряд электрона, а ![]() - расстояние от центра взрыва до точки наблюдения. Напряженность радиального электрического поля, соответствующая такому приращению потенциала, определяем по формуле:
- расстояние от центра взрыва до точки наблюдения. Напряженность радиального электрического поля, соответствующая такому приращению потенциала, определяем по формуле:
(1.2)
где
(1.3)
есть эквивалентный заряд взрыва. Под этой величиной нужно понимать превышение заряда электронного газа по сравнению с его равновесным значением при нулевой температуре.
Следует сказать, что при разогреве плазмы ионы тоже приобретают дополнительную скорость, однако, поскольку их масса значительно больше, чем масса электронов, приращением их зарядов можно пренебречь и считать их неподвижными.
В соответствии с формулой (1.2) напряженность радиального электрического поля в эпицентре взрыва при заданных выше параметрах составит ~ 7×105 В/м, на расстоянии в 870 км от этого места она будет ~ 1.5×105 В/м и на расстоянии 1300 км она составит ~ 6.5×104 В/м. Видно, что расчетные значения электрических полей на поверхности земли превышают значения, полученные во время испытаний. Отношение расчётных значений к измеренным составляют: в эпицентре взрыва – 13.5, на расстоянии 870 км от этого места – 4.5, на расстоянии 1300 км – 2.4. Конечно, неизвестна ни точная начальная температуры плазменного сгустка, ни масса бомбы и ракетоносителя, в котором ее подрывают, ни материалы, из которых изготовлены эти элементы. Корректируя эти данные, можно достаточно просто получить величины полей приближающиеся к экспериментальным значениям. Большее беспокойство вызывает то, что имеется большое несовпадение пространственных зависимостей экспериментальных и расчетных данных. Попытаемся объяснить причину таких расхождений.
Сначала рассмотрим случай, когда атмосфера отсутствует (рис. 5). Для упрощения задачи будем считать, что поверхностью Земли представляет идеально проводящая безграничная плоскость. Решение задачи распределения полей для заряда, находящегося над такой плоскостью, хорошо известно [16]. Горизонтальная составляющая электрического поля на поверхности такой плоскости равна нулю, а нормальная составляющая равна:
где ![]() - величина заряда,
- величина заряда, ![]() - кратчайшее расстояние от заряда до плоскости,
- кратчайшее расстояние от заряда до плоскости, ![]() - расстояние от точки наблюдения до точки пересечения вертикали, опущенной с точки, где находится заряд, на плоскость.
- расстояние от точки наблюдения до точки пересечения вертикали, опущенной с точки, где находится заряд, на плоскость.
Ниже проводящей плоскости электрические поля отсутствуют. Такая конфигурация полей связана с тем, что заряд, находящийся над проводящей плоскостью, индуцирует в ней такую поверхностную плотность зарядов, которая полностью компенсирует горизонтальную и вертикальную составляющую электрического поля заряда в проводящей плоскости. Зависимость величины поверхностного заряда от координаты ![]() можно определить, в данном случае, из соотношения:
можно определить, в данном случае, из соотношения:
(1.4)
Рис. 4. Отрицательный заряд над безграничной проводящей плоскостью.
Если проинтегрировать ![]() по координате
по координате ![]() , то получим величину заряда, находящегося над проводящей плоскостью. Таким образом, чтобы не пропустить электрические поля заряда
, то получим величину заряда, находящегося над проводящей плоскостью. Таким образом, чтобы не пропустить электрические поля заряда ![]() через проводящую плоскость, в ней должно содержаться количество свободных зарядов, дающих суммарный заряд не менее чем заряд
через проводящую плоскость, в ней должно содержаться количество свободных зарядов, дающих суммарный заряд не менее чем заряд ![]() . Если периодически приближать и удалять заряд от плоскости, то в ней возникнут периодические горизонтальные токи, которые будут создавать компенсирующие поверхностные заряды. Такой же эффект будет наблюдаться, если заряд в данной точке может рождаться и исчезать. Если в заданной точке над плоскостью вдруг за какое-то время возникнет заряд, то, для того, чтобы поля заряда не проникли через проводящую плоскость, за это же время на проводящей плоскости должны появиться компенсирующие заряды, соответствующие соотношению (1.4). Это означает, что величина токов, создающих компенсирующие заряды, будет тем больше, чем больше сам заряд и чем меньше время его возникновения. Если вычислить электрические поля по этой формуле, считая, что при
. Если периодически приближать и удалять заряд от плоскости, то в ней возникнут периодические горизонтальные токи, которые будут создавать компенсирующие поверхностные заряды. Такой же эффект будет наблюдаться, если заряд в данной точке может рождаться и исчезать. Если в заданной точке над плоскостью вдруг за какое-то время возникнет заряд, то, для того, чтобы поля заряда не проникли через проводящую плоскость, за это же время на проводящей плоскости должны появиться компенсирующие заряды, соответствующие соотношению (1.4). Это означает, что величина токов, создающих компенсирующие заряды, будет тем больше, чем больше сам заряд и чем меньше время его возникновения. Если вычислить электрические поля по этой формуле, считая, что при ![]() значение напряженности вертикальной составляющей электрического поля на поверхности равно 5.2 ×104 В/м, то на расстоянии 870 км получим значение поля 4×103 В/м, а на расстоянии 1300 км – 1.3×103 В/м. Видно, что значения расчетных полей и полученных экспериментально опять сильно отличаются от вычисленных. Это связано с тем, что между земной поверхностью и рассматриваемым зарядом существует ионосфера, которая тоже является проводником тока, хотя и не очень совершенным. Рассмотрим этот случай (рис. 5).
значение напряженности вертикальной составляющей электрического поля на поверхности равно 5.2 ×104 В/м, то на расстоянии 870 км получим значение поля 4×103 В/м, а на расстоянии 1300 км – 1.3×103 В/м. Видно, что значения расчетных полей и полученных экспериментально опять сильно отличаются от вычисленных. Это связано с тем, что между земной поверхностью и рассматриваемым зарядом существует ионосфера, которая тоже является проводником тока, хотя и не очень совершенным. Рассмотрим этот случай (рис. 5).
Рис. 5. Отрицательный заряд над поверхностью земли при наличии ионосферы.
Если заряд будет возникать в указанной на рисунке точке, то он будет собирать под собой имеющиеся в ионосфере свободные заряды противоположного знака для компенсации тех полей, которые он создает в ней. Однако если суммарное количество свободных положительных зарядов в ионосфере будет меньше, чем величина самого заряда, то их количества не хватит для полной компенсации полей возникающего заряда и его поля проникнут через ионосферу. При этом проникшие поля, в силу ее экранирующего действия ионосферы, могут быть значительно меньше, чем поля над ней. Всю эту картину можно описать только качественно, потому что точно не известна ни толщина ионосферы, ни степень ее ионизации по высоте, более того, такие задачи решаются только численными методами.
Сферичность ионосферы тоже накладывает свои особенности на процесс индукции компенсирующих поверхностных зарядов. Схематически этот процесс изображен на рис. 6.
Стремление возникающего заряда собрать под собой компенсирующие заряды приведет к продольной поляризации значительной части ионосферы. Компенсирующие положительные заряды будут находиться в ионосфере непосредственно в прямой видимости под зарядом и здесь их будет в избытке, в то время как за пределами прямой видимости в избытке будут отрицательные заряды. И вся система: заряд – ионосфера – земля получит дополнительный дипольный момент. Распределение наведенного заряда в ионосфере будет зависеть от высоты, на которой находится заряд, а также от положения Солнца по отношению к заряду, т.к. от его положения зависит степень ионизации ионосферы.
Рис. 6. Отрицательный заряд над поверхностью сферической ионосферы.
При ядерном взрыве синхронно с электрическими радиальными полями, двигающимися от плазменного сгустка со скоростью света, двигается и фронт рентгеновского излучения. Это излучение будет ионизировать атмосферу, увеличивая ее проводимость, а это, в свою очередь, увеличит защитные функции атмосферы от проникновения в неё ЭМИ. Кроме того, поскольку отрицательный потенциал плазменного сгустка в начальный момент взрыва очень большой, то из сгустка будет выброшено большое количество электронов, которые также через некоторое время попадут в ионосферу. Частичная нейтрализация электронов, попавших в ионосферу, произойдет, когда положительные ионы плазменного сгустка тоже достигнут ионосферы. Но это будет касаться только тех ионов, радиальная составляющая скорости которых была направлена в сторону ионосферы. Те же электроны и ионы, радиальная составляющая которых была направлена в сторону от нее, покинут пределы земного тяготения и будут представлять подобие того солнечного ветра, который является следствием испарения солнечной короны или вспышек на солнечной поверхности. Сейчас только схематически обрисованы те сложные процессы, которые сопутствуют ядерному взрыву, и предстоит еще большая работа, по воссозданию этих процессов для реальных условий. Очевидно, что сделать это можно только численными методами.
Рассмотренная модель говорит о том, что ядерный взрыв приведет не только к возникновению ИЭП в зоне прямой видимости, но и к глобальному возмущению ионосферы. Известно, что взрывы по программе «Starfish» и по программе «Программа К» привели к наличию больших помех радиотехническим и радиолокационным системам. Конечно, электрические поля в космосе, генерируемые таким взрывом имеют очень большие величиныи и представляют большую опасность для космических аппаратов. Величины максимальных значений напряженностей электрического поля, в зависимости от расстояния от эпицентра ядерного взрыва для нашего конкретного случая, представлены в таблице № 1.
Таблица № 1
| r(км) | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
|---|---|---|---|---|---|---|
| E(В/м) | 4х105 | 105 | 4,5х104 | 2,5х104 | 1,6х104 | 1,1х104 |
Теперь вернемся к горизонтальной составляющей электрических полей на земной поверхности, генерируемых при взрыве. Понятно, что эти поля представляют тангенциальную составляющую радиальных полей, идущих от точки взрыва. Именно эти поля и вызывают компенсирующие токи, которые создают компенсирующие поверхностные заряды. Можно вычислить порядок суммарных токов, которые будут иметь радиальную направленность по отношению к эпицентру взрыва. Для этого вычислим суммарный компенсирующий поверхностный заряд на поверхности земли, который должен образоваться при взрыве атомного заряда. Этот заряд равен заряду плазменного сгустка с обратным знаком
Проведя вычисления по этой формуле, исходя из реально измеренных вертикальных напряженностей электрических полей в эпицентре взрыва (5.2×104 В/м), при расстоянии до взрыва 400 км получаем заряд ~ 106 Кл. Значение же заряда, вычисленное по формуле (1.3) составят ~ 1.2×107 Кл. Такое расхождение, как уже сказано, может быть связано с экранирующим действием ионосферы. Из данных по топологии ИЭП, приведенных на рис. 3, следует, что время нарастания импульса электрического поля составляет ~ 50 нс. Это означает, что суммарный ток, направленный к эпицентру взрыва, должен составлять ~ 1012 ампер. Конечно, эта цифра несколько завышена, потому что компенсирующие заряды притягиваются не к одной точке, являющейся эпицентром взрыва, а к достаточно обширной области в его окрестности. Но даже, если эту величину уменьшить на несколько порядков, то по-прежнему величина компенсирующих токов будет очень большой. Теперь понятно, почему на острове Оаху, находящемся на расстоянии 1300 км от места взрыва, сгорели 300 уличных фонарей, а близ Джесказгана в воздушной телефонной линии протяженностью 570 км возникли токи ~ 2.5 кА и сгорели все плавкие предохранители. Даже на силовой кабель протяженностью более 1000 км, соединяющий Алма-ату и Акмолу, и имеющий бронированный экран из свинца, оплетку из стальной ленты, и находящийся на глубине 0.8 м, возникли такие наводки, что сработали автоматы, отключив от кабеля электростанцию. Конечно, импульс тангенциальных токов, не менее значительный, чем на земной поверхности, будет и в ионосфере, что приведет к ее возмущению в глобальных масштабах.
Теперь весь процесс формирования ИЭП при взрыве заряда в космосе можно описать следующим образом. В момент взрыва за время детонации ядерного заряда, которое длится несколько наносекунд, образуется плотный сгусток плазмы с температурой в несколько десятков и даже сотен миллионов градусов. Этот сгусток генерирует мощное гамма излучение, которое распространяется во все стороны от сгустка со скоростью света. Одновременно генерируется радиальное электрическое поле, которое также распространяется в радиальном направлении от сгустка со скоростью света. Радиальные электрические поля ИЭП и гамма-излучение достигают ионосферы одновременно. При своем дальнейшем движении в сторону поверхности земли, если мощности взрыва для этого достаточно, рентгеновское излучение начинает ионизировать и слои атмосферы, находящиеся ниже ионосферы. Одновременно будут происходить процесс ионизации верхних слоев атмосферы и проникновения в них радиального электрического поля. В ионизированных слоях за счет наличия радиального электрического поля возникнут радиальные токи, которые приведут к расслоению зарядов и к вертикальной поляризации проводящих слоев. Процессы поляризации атмосферы будут длиться столько времени, сколько будет существовать радиальное поле, а также проводимость ионизированного воздуха. Поскольку ионосфера не сможет обеспечить заряд, необходимый для полной компенсации радиального поля плазменного сгустка, эти поля, хотя и в ослабленном виде, будут продолжать распространяться в направлении земной поверхности. Достигнув её, электрические поля создадут мощные радиальные токи. Процесс распространения рентгеновского излучения и радиальных полей через ионосферу приведет к ее дополнительной ионизации и поляризации, а также к появлению импульса тангенциальных токов. Импульс тангенциальных токов в ионосфере будет распространяться на расстояния значительно большие, чем зона видимости взрыва, что приведет к глобальным возмущениям ионосферы.
С некоторым запозданием по фазе ионосферы достигнут и электроны, выброшенные из плазменного сгустка, что приведет к дополнительным её возмущениям. И если мощность взрыва такова, что ионизованными окажутся даже нижние слои атмосферы, то разделение зарядов, а, следовательно, и наведенное, за счет разделения зарядов, электрическое поле будет иметь место во всей атмосфере.
К тому моменту, когда поток жесткого гамма излучения и ионизация атмосферы прекратятся, часть атмосферы, ионизованной ниже, чем существующая граница ионосферы, перестанет быть проводником, а, следовательно, пространственно разделенные заряды окажутся запертыми в ней. Запертые в атмосфере электроны по-прежнему будут создавать какую-то статическую разность потенциалов, которая будет медленно релаксировать в меру наличия какой-то остаточной проводимости атмосферы. Следует отметить, что полярность этого поля будет противоположна полярности первоначального ИЭП. Это означает, что радиальное электрическое поле, наблюдаемое на поверхности земли, сначала будет направлено от земли к эпицентру взрыва, но в какой-то момент времени оно изменят свою полярность. Именно такое поведение электрического поля наблюдается на графике, изображенном в верхнем правом углу рис. 3.
Становится понятным и то, почему после космического ядерного взрыва еще длительное время наблюдается остаточное свечение атмосферы под местом взрыва. Это свечение обязано тем электронам, которые на первом этапе развития ЭМИ были перемещены из ионосферы в более плотные слои атмосферы, а затем, после прекращения ионизируещего действия гамма излучения, остались запертыми в мало проводящей атмосфере, продолжая её ионизировать.
Теперь обратимся к рис. 3. Поскольку величина радиального поля в соответствии с соотношением (1.2) пропорциональна произведению количества свободных электронов на температуру плазмы, то по этому графику можно судить о процессах детонации ядерного заряда и последующем охлаждении плазменного сгустка. Из рисунка видно, что наиболее активный процесс формирования ИЭП длится всего ~ 100 нс. При этом даже рентгеновские лучи, распространяющиеся со скоростью света, успеют уйти от центра взрыва всего на 30 м. На рисунке есть две зависимости. Сплошной линией обозначена кривая, сфотографированная с экрана осциллографа, пунктирная линия представляет реальную форму импульса, полученную путем обработки сфотографированной кривой с учетом параметров входных цепей осциллографа. На начальном этапе реальной зависимости на протяжении прядка 50 нс видны два последовательных пика. Первый пик представляет взрыв атомной бомбы, поджигающей термоядерный заряд, второй пик представляет процесс детонации термоядерного топлива. Далее идет быстрый спад, который характеризует процесс охлаждения самого сгустка. Видно, что он происходит очень быстро. Естественно предположить, что это тот период, когда основные потери энергии связаны с лучистыми потерями за счет жесткого рентгеновского излучения. На зависимости, изображенной на графике, расположенном в верхнем правом углу рис. 3, изображены процессы в промежутке времени исчисляемом секундами после взрыва. Видно, что интенсивность этих процессов незначительна, однако, характерной особенностью является то, что напряженность поля меняет свой знак.
Проведенный анализ свидетельствует о том, что возникновение ЭМИ нужно рассматривать как быстро протекающее рождение нового отрицательного однополярного заряда в момент детонации ядерного заряда и последующее более медленное его исчезновение при охлаждении плазмы.
Таким образом, наличие ИЭП при ядерном взрыве являются свойствами самого взрыва, а не вторичными явлениями. Его свойства и характеристики могут быть объяснены в рамках концепции скалярно-векторного потенциала. Изучая же топологию ИЭП, можно изучать процессы детонации при ядерном взрыве, причем данный метод является дистанционным. Изучая топологию ИЭП на земной поверхности, можно судить также о последующих процессах поляризации и деполяризации ионосферы, атмосферы и земной поверхности. При взрыве в атмосфере сам процесс взрыва и его развитие связаны с наличием атмосферы, и это будет также накладывать свои особенности на формирование ИЭП.
Теперь следует сделать одно замечание по поводу самого термина электромагнитный импульс (ЭМИ). Из этого названия следует исключить слово магнитный, т.к. данный процесс представляет распространение только радиальных электрических полей, и при таком процессе магнитные поля отсутствуют. Другое дело, что электрические поля могут наводить в окружающих проводящих средах токи, и эти токи будут генерировать магнитные поля, но это уже вторичное явление.
Казалось бы, все очень хорошо сходится, однако, есть один существенный вопрос, который пока не рассмотрен, он касается баланса энергий при взрыве. Если считать, что одна тонна тротила эквивалентна 4.6×109 Дж, то при взрыве бомбы с тротиловым эквивалентом 1,4 Мт при ее взрыве выделяется 6.44×1015 Дж. Если считать, как следует из рис. 2, что время детонации составило 50 нс, то мощность взрыва составляет ~1.3×1023 Вт. Для примера скажем, что мощность излучения Солнца составляет 3.9×1026 Вт. Рассмотрим вопрос, куда и каким образом, за столь короткое время, может быть израсходована энергия, выделенная при таком взрыве.
В соответствии с уравнением Стефана- Больцмана мощность, излучаемая нагретой поверхностью, пропорциональна четвертой степени ее температуры:
где  - постоянная Стефана- Больцмана, а
- постоянная Стефана- Больцмана, а ![]() - площадь излучающей поверхности.
- площадь излучающей поверхности.
Если взять начальную температуру плазменного сгустка ~108 К, то при начальном его диаметре 1 м (при этом площадь поверхности сгустка составляет ~3 м2) вся энергия взрыва будет излучена за время ~ 0.4 нс. Если же взять начальную температуру ~107, то это время будет составлять уже ~ 400 нс. Таким образом следует положить, что начальная температура плазменного сгустка находиться где-то между взятыми значениями. Длина волны, на которой будет излучено максимальное количество энергии, определяется законом Вина
Если подставить сюда значение температуры 5×107 К, то получим длину волны порядка 6 Å, что соответствует жесткому рентгеновскому излучению. Таким образом, в период самого активного выделения энергии взрыва сам взрыв будет невидимым в видимой части спектра. По мере охлаждения сгустка его температура начнет падать и ![]() начнет сдвигаться в видимую часть спектра. При этом будет наблюдаться интересное явление, когда температура сгустка будет падать, а видимая яркость будет расти.
начнет сдвигаться в видимую часть спектра. При этом будет наблюдаться интересное явление, когда температура сгустка будет падать, а видимая яркость будет расти.
Но рассмотренный механизм потерь не является единственным. Поскольку с температурой сгустка однозначно связаны и его электрические поля, то сразу после детонации они будут максимальны, а затем с падением температуры сгустка начнут уменьшаться пропорционально температуре. Однако энергия, необходимая для их создания, будет падать не так быстро, как энергия необходимая для создания рентгеновского излучения.
Кроме этих потерь будут еще потери на термоэмиссию электронов из плазменного сгустка. Скорость электронов, которые будут покидать сгусток значительно меньше, чем скорость электрических полей т.к. она соответствует температуре сгустка, поэтому фронт этих электронов будет существенно запаздывать относительно фронтов рентгеновского излучения и радиального электрического поля. И только после того, как термоэлектроны покинут сгусток, основной запас энергии ядерного взрыва будет исчерпан. Останутся только ионы с каким-то количеством компенсирующих электронов, которые будут разлетаться в радиальном направлении от места взрыва. Этот оставшийся реликт ядерного взрыва будет представлять шаровую молнию.
Возникает еще один немаловажный вопрос о том, какое количество электронов покинет плазменный сгусток. Для того чтобы ответить на него, рассмотрим условие электронейтральности плазмы. В тот момент, когда металл превращается в плазму, происходит не только переход вещества из одного агрегатного состояния в другое, но и меняется статистика описания электронного газа. В твердом состоянии это статистика Ферми-Дирака, а в состоянии плазмы - это статистика Больцмана. Когда электронный газ находился в твердом проводнике, то в состоянии электронейтральности на каждый ион приходилось по одному свободному электрону. Определим с точки зрения концепции скалярно-векторного потенциала, какое соотношение должно соблюдаться между электронами и ионами в плазме, чтобы она тоже оставалась электронейтральной. До того, как твердое вещество превратилось в плазму, плотность электронов и ионов была одинаковой и, следовательно, абсолютные величины их зарядов были равны, т.е.
После превращения вещества в плазму общий эквивалентный заряд электронов увеличился, на величину, определяемую соотношением (1.3), а у ионов остался практически прежним. Теперь уже для соблюдения электронейтральности должно соблюдаться соотношение:
где ![]() - равновесное количество электронов в плазме.
- равновесное количество электронов в плазме.
Видно, что это равновесное количество меньше, чем до перехода вещества в состояние плазмы. Разница составляет
(1.5)
Например, при температуре ~108 величина, стоящая в скобках, составит примерно 0.13. Это означает, что при указанной температуре, для сохранения электронейтральности плазмы, 13 % от общего первоначального количества электронов должны будут ее покинуть. Будем называть этот эффект эффектом временно лишних электронов. Слово «временно» используется в том смысле, что временными они являются до тех пор, пока плазма является горячей. В этой связи понятным становиться то, откуда, например, на поверхности Солнца возникают мощные магнитные поля, особенно в тех случаях, когда на нем появляются пятна. Эти поля индуцируются теми токами, которые перетекают между областями плазмы, имеющими различную температуру.
Мы достаточно подробно рассмотрели поведение статического заряда над проводящей плоскостью. Но в действительности имеется не статический заряд, а заряд, который живет всего несколько сот наносекунд. Поэтому и процессы кратковременного рождения и исчезновения заряда отличаются от тех, которые рассмотрены. Проведенный анализ был направлен на то, чтобы лучше понять кинематику самого процесса.
Если в начале координат расположен заряд ![]() , зависящий от времени, то электрические поля, создаваемые им в окружающем пространстве могут быть найдены из соотношения:
, зависящий от времени, то электрические поля, создаваемые им в окружающем пространстве могут быть найдены из соотношения:
(1.6)
которому соответствуют запаздывающие продольное электрические поля:
(1.7)
В соответствии с соотношениями (1.6,1.7) короткоживущий заряд порождает столь же кратковременный импульс продольных электрических полей, которые в пространстве распространяются со скоростью света и образуют сферический слой, толщина которого равна времени существования заряда, умноженному на скорость света. Если для нашего случая принять, что время жизни заряда составляет полуширину импульса ИЭП (где-то около 150 нс), то толщина этого слоя составит около 45 м. Сферический слой, достигнув сначала ионосферы, а затем земли наведет там такие же радиальные токи, как если бы статический заряд появился и, просуществовав 150 нс, исчез.
Проведенное рассмотрение хорошо согласуется с результатами экспериментальных данных, полученных в процессе ядерных испытаний в космосе. Однако оно противоречит СТО, поскольку хоть в СТО скалярный потенциал заряда и зависит от скорости, однако ввиду наличия лорецевого сокращения размеров материальных объектов в направлении своего движения, сам заряд остаётся инвариантом скорости.
Образование статических электрических полей вокруг сверхпроводящих соленоидов и торов
Эксперименты, проведенные с сверхпроводящими соленоидами и торами, в которые индукционным способом вводились постоянные токи показали, что вокруг них образуются статические электрические поля. Эти данные свидетельствуют о зависимости величины заряда от их относительной скорости, что также противоречит СТО.
В соответствии с концепцией скалярно-векторного потенциала [2-4] радиальное поле, генерируемое электронами движущимся по проводнику, определяется соотношением:
(2.1)
где ![]() - удельный заряд электронов, приходящихся на единицу длины проводника,
- удельный заряд электронов, приходящихся на единицу длины проводника, ![]() - их скорость,
- их скорость, ![]() - расстояние от проводника до точки наблюдения.
- расстояние от проводника до точки наблюдения.
Это эквивалентно появлению на проводнике дополнительного отрицательного потенциала, что, в свою очередь, равноценно появлению на этом проводнике удельного статического заряда
(2.2)
Однако до настоящего времени никто не получал экспериментального подтверждения справедливость соотношений (2.1) и (2.2).
В то время, когда Фарадеем и Максвеллом были сформулированы основные законы электродинамики, экспериментально подтвердить соотношение (2.1) было невозможно, т.к. плотности токов, достижимые в обычных проводниках, слишком малы для экспериментального обнаружения рассматриваемого эффекта. Таким образом, положение о независимости скалярного потенциала и заряда от скорости и последующее введение магнитного поля были сделаны волевым путём на феноменологической основе.
Плотности токов, которые могут быть достигнуты в сверхпроводниках, позволяют экспериментально обнаружить электрические поля, определяемые соотношением (2.1) [2-4, 6-9].
Рассмотрим постановку эксперимента, который должен дать ответ на поставленные вопросы. Схема эксперимента изображена на рис. 7 [3-4].
Рис. 7. Схема эксперимента по обнаружению зависимости величины скалярного потенциала и величины заряда от скорости носителей тока.
Для целей введения тока в сверхпроводящую малоиндуктивную обмотку был использован охлаждаемый до гелиевых температур трансформатор с железным сердечником. Используя в качестве вторичной обмотки трансформатора сверхпроводящую обмотку, соединенную с малоиндуктивным соленоидом, можно без наличия гальванических контактов вводить ток в соленоид. В трансформаторе использовался кольцеобразный сердечник из трансформаторной стали с поперечным сечением 9 см2. Первичная и вторичная обмотки трансформатора были намотаны ниобий-титановым проводом с медным покрытием и содержали 150 и 10 витков соответственно. Таким образом, трансформатор имеет коэффициент трансформации 15. Диаметр проволоки составлял 0.25 мм. Вторичная обмотка трансформатора соединена последовательно с малоиндуктивным соленоидом, который намотан бифилярно и содержит 2448 витков такого же провода. Общая длина намотки составляет 910 м. Концы соленоида и вторичной обмотки трансформатора сварены при помощи лазерной сварки. Соленоид намотан на каркасе из фторопласта. Внутренний и внешний диаметр обмотки соленоида 35 и 90 мм соответственно, ширина намотки 30 мм. К средней точке соленоида подключен внутренний провод коаксиала, выходящего наружу криостата, такой же коаксиал подключен и к экрану соленоида. Конструкция малоиндуктивного соленоида показана на рис.8.
Рис. 8. Конструкция малоиндуктивного сверхпроводящего соленоида: 1 - алюминиевый каркас, 2 - фторопластовая втулка, 3 - фторопластовый диск, 4 - скоба, 5 - стойки, 6 - болт, 7 - медный экран, 8 - фторопластовый каркас.
Он намотан на фторопластовом каркасе 8, который заключён в алюминиевый каркас 1. Снаружи соленоид окружён медным экраном 7, который совместно с каркасом 1 является экраном соленоида. К каркасу 1 посредством болта 6 и фторопластовой втулки 2 крепится фторопластовый диск 3, на котором смонтирована скоба 4. Витки вторичной обмотки трансформатора охватывают скобу 4, через которую, не касаясь её, проходит магнитопровод трансформатора. Вся конструкция крепится к трансформатору посредством стоек 5. Трансформатор совместно с соленоидом размещается в баке гелиевого криостата.
Схема подключения коаксиалов к безиндуктивному соленоиду показана на рис. 9.
Сопротивление между заземленными элементами, экраном соленоида и самим соленоидом составляет не менее 1014 Ом. Элементы, используемые в конструкции, имели следующие емкости относительно земли: коаксиал 3 – 44 пФ, коаксиал 4 – 27 пФ, емкость экран – земля составляет – 34 пФ, емкость экран–соленоид составляет – 45 пФ, В качестве электрометра использовался емкостной вибрационный электрометр с входной емкостью 60 пФ и входным сопротивлением 1014 Ом.
Рис. 9. Схема соединения малоиндуктивного соленоида: 1 - малоиндуктивный соленоид, 2 - экран соленоида, 3,4 - коаксиалы, 5 - общий экран, которым является гелиевый бак.
При такой конструкции сверхпроводящего соленоида и окружающего его экрана нельзя произвести точный электродинамический расчет электростатических полей, возникающих вокруг соленоида, однако, установить наличие самого эффекта, такая конструкция позволяет.
При измерениях электрометр подключался непосредственно к экрану посредством коаксиала 4, а средняя точка сверхпроводящего соленоидоа посредством коаксиал 3 заземлялась. Ток в первичную обмотку трансформатора вводился от источника постоянного тока, показания электрометра при этом не зависели от направления тока. При величинах вводимого тока ~ 9 А происходил самопроизвольный сброс показаний электрометра. Это означает, что ток в обмотке соленоида достигал своего критического значения, и обмотка переходила в нормальное состояние. Железный сердечник при этом захватывал магнитный поток и при уменьшении вводимого в соленоид тока, кривая зависимости измеряемого потенциала от тока повторялась, а потенциал достигал своего максимального значения при нулевом значении тока.
При этом зависимости потенциала от тока оказывались полностью обратимыми, это свидетельствовало о том, что при захвате потока железным сердечником не происходило его магнитное насыщение. Полученная экспериментальная зависимость измеряемой разности потенциалов приведена на рис. 10.
Рис. 10. Зависимость разности потенциалов между экраном и малоиндуктивным соленоидом от тока, вводимого в первичную обмотку трансформатора.
Данные эксперимента приведены в таблице № 2.
Таблица № 2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | |
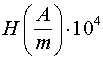
|
1.91 | 3.82 | 5.73 | 7.64 | 9.55 | 11.5 | 14.6 | 15.3 |
| 2 | 6 | 10 | 15 | 21 | 27 | 35 | ||
| 7 | 20 | 34 | 50 | 71 | 90 | 117 | ||
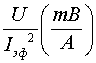
|
1.75 | 2.22 | 2.13 | 2.00 | 1.94 | 1.84 | 1.83 |
В первой графе таблицы приведены значения тока, вводимого в первичную обмотку трансформатора ![]() . Во второй графе даны значения тока
. Во второй графе даны значения тока ![]() в обмотке соленоида, рассчитанные исходя из значения коэффициента трансформации равного 15. При этом предполагается, что во всем диапазоне вводимых токов намагниченность сердечника остается пропорциональной току. В третьей графе даны значения магнитных полей на поверхности сверхпроводящих проводов соленоида. В четвертой - приведены показания электрометра. В пятой - приведены эффективные значения разности потенциалов, которые были бы между соленоидом и экраном до подключения к последнему суммарной емкости коаксиала и электрометра. В шестой - дан коэффициент
в обмотке соленоида, рассчитанные исходя из значения коэффициента трансформации равного 15. При этом предполагается, что во всем диапазоне вводимых токов намагниченность сердечника остается пропорциональной току. В третьей графе даны значения магнитных полей на поверхности сверхпроводящих проводов соленоида. В четвертой - приведены показания электрометра. В пятой - приведены эффективные значения разности потенциалов, которые были бы между соленоидом и экраном до подключения к последнему суммарной емкости коаксиала и электрометра. В шестой - дан коэффициент 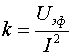 , указывающий на отклонение полученной зависимости от квадратичного закона. Коэффициент
, указывающий на отклонение полученной зависимости от квадратичного закона. Коэффициент ![]() составил величину 3.35 исходя из того, что емкость между экраном и соленоидом составила 45 пФ, а суммарная входная ёмкость электрометра была равна 111 пФ. Среднеквадратичное относительное отклонение коэффициента
составил величину 3.35 исходя из того, что емкость между экраном и соленоидом составила 45 пФ, а суммарная входная ёмкость электрометра была равна 111 пФ. Среднеквадратичное относительное отклонение коэффициента ![]() от своего среднего значения равного 1.93 составляет 0.13, что дает относительную среднеквадратичную погрешность 7%. Таким образом, полученная зависимость между током и измеряемым значением потенциала очень близка к квадратичному закону. Таким образом, экспериментальные результаты указывают на то, что величина скалярного потенциала, а, следовательно, и заряда зависит от скорости.
от своего среднего значения равного 1.93 составляет 0.13, что дает относительную среднеквадратичную погрешность 7%. Таким образом, полученная зависимость между током и измеряемым значением потенциала очень близка к квадратичному закону. Таким образом, экспериментальные результаты указывают на то, что величина скалярного потенциала, а, следовательно, и заряда зависит от скорости.
Однако в данной схеме эксперимента имеет место непосредственное гальваническое подключение электрометра к сверхпроводящему соленоиду. Это может вызвать вопросы, а не являются ли причиной возникновения разности потенциалов между соленоидом и экраном какие-то контактные явления в месте контакта провода, соединяющего электрометр с соленоидом?
Для ответа на этот вопрос были проведены эксперименты со сверхпроводящим ниобиевым тором.
Схема эксперимента показана на рис. 11.
Если внутри проводящего экрана разместить второй проводящий экран, и между ними подключим электрометр, то в том случае, когда внутри внутреннего экрана появится заряд, между внутренним и наружным экраном появится разность потенциалов. В эксперименте, в качестве наружного экрана 1, использовалось ярмо трансформатора, выполненное из трансформаторной стали. На центральном стержне этого ярма располагалась первичная обмотка 2, намотанная ниобий-титановым проводом, содержащая 1860 витков. На этом же стержне располагался торообразный металлический экран 3, выполненный из меди. Внутри этого экрана был расположен тор 4, выполненный из ниобия. Наружный диаметр ниобиевого тора составлял 76 мм, а внутренний 49 мм. Трансформатор размещался в баке гелиевого криостата и охлаждался до гелиевой температуры, при этом ярмо трансформатора и гелиевый бак заземлялись. При введении постоянного тока в первичную обмотку трансформатора в сверхпроводящем торе индуцировался ток, и электрометр фиксировал появление между экраном 3 и ярмом трансформатора разность потенциалов ![]() . Это означает, что ниобиевый тор, расположенный внутри экрана 3 при введении в него постоянного тока перестаёт быть электронейтральным. Величина постоянного тока в сверхпроводящем торе в 1860 раз превышала ток, вводимый в первичную обмотку трансформатора.
. Это означает, что ниобиевый тор, расположенный внутри экрана 3 при введении в него постоянного тока перестаёт быть электронейтральным. Величина постоянного тока в сверхпроводящем торе в 1860 раз превышала ток, вводимый в первичную обмотку трансформатора.
Рис. 11. Схема эксперимента со сверхпроводящим тором, изготовленным из ниобия.
Зависимость разности потенциалов ![]() от тока
от тока ![]() , вводимого в первичную обмотку трансформатора, показана на рис. 12.
, вводимого в первичную обмотку трансформатора, показана на рис. 12.
Полученные значения разности потенциалов, по сравнению со случаем сверхпроводящей проволочной обмотки, оказались значительно меньшими, это связано со значительно меньшей поверхностью тора, по сравнению с поверхностью проволочной обмотки. Вид зависимости разности потенциалов от вводимого тока также сильно отличается. Квадратичный участок наблюдается только на очень небольшом начальном участке вплоть до значений токов около 2 ампер, вводимых в первичную обмотку. Далее эта зависимость становится прямолинейной с малым углом наклона по отношению к оси абсцисс. К тому же срыва показаний электрометра в данном случае не наблюдалось.
Рис. 12. Зависимость разности потенциалов межу экраном 3 и ярмом трансформатора 1 от тока, вводимого в первичную обмотку трансформатора.
С чем связаны такие отличия поведения разности потенциалов по сравнению с проволочным вариантом? В случае проволочного соленоида сверхпроводящий ток равномерно распределён по поверхности проволоки и достигает своего критического значения на всех её участках одновременно, с чем и связан одновременный переход всей обмотки соленоида в нормальное состояние, при достижении в проволоке на каком то участке критического значения тока.
В случае тора процесс установления сверхпроводящего тока на его поверхности происходит по-другому. Вводимый в сверхпроводящий тор постоянный ток очень неравномерно распределён по его поверхности. Максимальные плотности тока имеют место на внутренней поверхности тора, а на периферии они значительно меньше. С этим связано то, что внутренние поверхности тора начинают переходить в нормальное состояние раньше, чем наружные. Процесс перехода тора в нормальное состояние происходит таким образом, что при увеличении тока в торе в нормальное состояние переходят сначала внутренние области и нормальная фаза начинает перемещаться от внутренних областей к наружным. Процесс длится до тех пор, пока весь тор не перейдёт в нормальное состояние. Но почему при этом к моменту перехода тора в нормальное состояние не происходит сброс тока, как это имеет место в случае проволочного соленоида? Это связано с тем, что ниобий является сверхпроводником второго рода и он не сразу скачком переходит в нормальное состояние, а у него имеется достаточно значительная область плотностей токов, при которых он находится в смешанном состоянии, когда внутрь массивного проводника проникают вихри Абрикосова. Следовательно, то обстоятельство, что показания электрометра не имеют сброса показаний, указывает на то, что сверхпроводящий тор находится в смешанном состоянии, а вихревые структуры, которые также представляют сверхпроводящие токи, приводят к тому, что тор перестаёт быть электронейтральным. Из вышеперечисленного можно сделать вывод, что вихри несут на себе не только кванты магнитного потока, но ещё и квантованные электрические заряды.
Если изменить направление тока в первичной обмотке, то зависимость, подобная изображённой на рис. 12, повторяется, однако, наблюдается сильный гистерезис. Это связано с тем, что вихри, проникшие вглубь сверхпроводника, закрепляются на дефектах кристаллической структуры, попадая в потенциальные ямы, что и приводит к гистерезису.
Таким образом, результаты проведенных экспериментов однозначно указывают на зависимость скалярного потенциала и величины зарядов от их скорости, что было предсказано ещё в работе [6] и экспериментально подтверждено в работе [8].
Все указанные эксперименты были проведены в начале 90-х годов в МГП НИИ криогенного приборостроения при ФТИНТ НАН Украины.
Литература
- 1.Знакомый и незнакомый Зельдович (в воспоминаниях друзей, коллег, учеников), М: Наука, 1993, 352 с. (под редакцией С. С. Герштейна и Р.А. Сюняева).
- 2. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с. ISBN – 966-7983-55-2.
- 3. Менде Ф. Ф. Непротиворечивая электродинамика и угроза ядерного космического терроризма. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-9
- 4. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 5. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.
- 6. Менде Ф. Ф. К вопросу о возникновении вторичных электрических полей при протекании через сверхпроводники постоянных токов. - Харьков, 1992.- 28 с. Рукопись депонирована в ВИНИТИ 05.11.92, № 3182-В92. Деп.
- 7. Менде Ф. Ф. К вопросу о зависимости величины заряда электронов от скорости при протекании через сверхпроводники постоянных токов. Препринт 1–93. МГП НИИ КП при НТК ФТИНТ АН Украины, 1993 г. - 45 с.
- 8. Mende F. F. Experimental corroboration and theoretical interpretation of dependence of charge value on DC flow velocity through superconductors. Proceedings International Conference “Physics in Ukraine”, Kiev, 1993.
- 9. Mende F. F. Conception of the scalar-vector potential in contemporary electrodynamics, arXiv, physics/0506083.