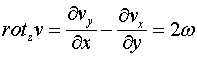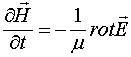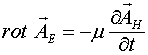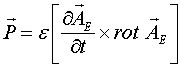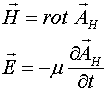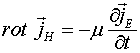Физические векторы и векторы фантомы
Физические векторы и векторы фантомы. Множественность форм записи электродинамических законов.
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Векторный анализ является основным математическим аппаратом, используемым в электродинамике. Такие векторные величины, как сила, скорость, ускорение, электрическое поле и ток хорошо демонстрируют физический характер этих величин. Однако при использовании векторного аппарата для описания физических процессов вводятся и такие вектора, которые не отражают физической сущности тех процессов, которые они описывают. Такие векторы будем называть векторами-фантомами.
Приведём несколько примеров.
Если имеется диск, вращающийся с угловой скоростью ![]() , то этот процесс изображают в качестве вектора, который совпадает с осью вращения диска и опирается на его центр. Спрашивается, существует ли такой вектор на самом деле и что он представляет? Нет сомнения в том, что по договоренности такой вектор можно ввести, но какого-либо физического смысла, как, например, вектор скорости, он не имеет. Таким точно образом вводится вектор механического момента. Этот вектор тоже совпадает с осью вращения, опирается на центр плоскости вращения и равен произведению радиальной скорости на радиус. Подобным образом вводится и вектор магнитного дипольного момента, который для кругового тока равен произведению величины тока на площадь обтекаемого током круга. Этот вектор совпадает с осью вращения круга и опирается на его плоскость. Но какого-либо физического смысла эти вектора не имеют.
, то этот процесс изображают в качестве вектора, который совпадает с осью вращения диска и опирается на его центр. Спрашивается, существует ли такой вектор на самом деле и что он представляет? Нет сомнения в том, что по договоренности такой вектор можно ввести, но какого-либо физического смысла, как, например, вектор скорости, он не имеет. Таким точно образом вводится вектор механического момента. Этот вектор тоже совпадает с осью вращения, опирается на центр плоскости вращения и равен произведению радиальной скорости на радиус. Подобным образом вводится и вектор магнитного дипольного момента, который для кругового тока равен произведению величины тока на площадь обтекаемого током круга. Этот вектор совпадает с осью вращения круга и опирается на его плоскость. Но какого-либо физического смысла эти вектора не имеют.
Вспомним, что такое вектор, представляющий ротор. Этот вектор вводится следующим образом
Чтобы выяснить геометрический смысл ротора рассмотрим твердое тело, которое с угловой скоростью ![]() вращается вокруг оси
вращается вокруг оси ![]() . Тогда линейная скорость тела
. Тогда линейная скорость тела ![]() в точке (
в точке (![]() ,
, ![]() ,
, ![]() ) будет численно равна
) будет численно равна
а слагающие её по осям, для правовинтовой системы координат, будут равны
Слагающие вектора ![]() при этом определяться соотношениями:
при этом определяться соотношениями:
И снова получен вектор, направленный параллельно оси вращения и нормальный к плоскости вращения. Этот вектор тоже вводится по договорённости и какого-либо физического смысла не имеет.
Те же рассуждения можно распространить и на векторное произведение.
Таким образом, при использовании векторного исчисления для описания физических явлений вводятся два типа векторов. Первый из них представляет реальные физические вектора, которые характеризуют саму физическую величину с учётом её величины и направления (например, вектора силы, скорости, ускорения, напряженности электрического поля и тока). Другая же категория векторов – это те векторы, которые можно представить с помощью операции ротора или векторного произведения. Они физические вектора не представляют и вводятся по договорённости, являясь векторами-фантомами. Именно к вектору такого типа и относится магнитное поле.
Действительно, магнитное поле вводят или при помощи ротора электрического поля
или как ротор векторного потенциала
Это означает, что магнитное поле не является физическим полем, а представляет некий векторный символ, который вводят по договорённости и физического смысла не имеет.
Что же происходит далее? При записи уравнений Максвелла ротор от магнитного поля приравнивают полному току
и получается так, что ротор от вектора, который вводят по договорённости, даёт реальный физический вектор. Таким образом, вектор магнитного поля представляет типичный вектор фантом.
Можно привести и другой пример. Силу Лоренца, действующую на движущийся заряд, определяют векторным произведением реального вектора скорости и магнитного поля:
Опять получается так, что операция векторного произведения, которая сама по себе физического смысла не имеет, действуя на вектор, не имеющий физического смысла, даёт реальную физическую силу с учётом её величины и направления. В этом и состоит смысл введения векторов фантомов в векторном исчислении. Если посмотреть на математический аппарат физики применительно к векторному исчислению, то оказывается, что этот аппарат представляет смесь реальных физических векторов и векторов фантомов.
Но тогда возникает вопрос, а можно ли вообще исключить из обихода векторы-фантомы, которые вводят только по договорённости и построить электродинамику без их использования. В работах
- http://fmnauka.narod.ru/asd.pdf
- http://fmnauka.narod.ru/Pro1.pdf
- http://arxiv.org/abs/physics/0402084
- http://arxiv.org/abs/physics/0506083
показано, что вся электродинамика может быть построена без использования такого понятия как магнитное поле. При этом в её основу должны быть положены такие фундаментальные понятия как электрическое поле, которое является градиентом скалярного потенциала, а также векторный потенциал, причиной появления которого есть зависимость скалярного потенциала заряда от скорости его относительного движения. Такой подход - это революция в классической электродинамике. Он ставит во главу классической электродинамики скалярный потенциал заряда и его зависимость от скорости и лишает прав физического поля магнитное поле, а также исключает необходимость использование СТО, т.к. все существующие явления в электродинамике находят своё объяснение без её использования.
Понятие магнитного поля как реального вектора существует с тех пор, как учёные заметили, сколь организованно ведут себя железные опилки вблизи магнитов или кольцевых токов. Такое их поведение казалось почти очевидным следствием наличия какого-то силового вектора, действующего на них. И таким вектором было признано магнитное поле. Однако, очевидное не всегда является реальным. Оказывается, что такое поведение железных опилок связано совсем не с существованием магнитного поля как физического вектора, а с тем, что токи обладают потенциальной энергией по отношению к другу к другу, и эта энергия для случая устойчивого равновесия всегда стремится к минимуму. Именно по этой причине железные опилки, в которых отдельные атомы представляют микроскопические кольцевые токи, и ведут себя таким образом. Все эти вопросы рассмотрены в работах [1-9] и с их появлением закончился очень важный и очень противоречивый этап в развитии современной физики, и перед ней открываются новые неизведанные горизонты. Но история физики и человеческого прогресса говорит нам о том, что такие события не могут быть осознанны обществом сразу, так было с Джордано Бруно, так было с Коперником и Галилеем.
Продолжая рассмотрение этого вопроса, нельзя не заметить, что использование векторов-фантомов приводит к большой неоднозначности при формулировке законов электродинамики. Поскольку всегда можно положить
(1)
(2)
то уравнения Максвелла можно записать в терминах новых потенциалов:
(3)
(4)
Для каждого из введённых потенциалов можно получить волновое уравнение, в частности
(5)
и считать, что в пространстве распространяются не магнитные и электрические поля, а поле электрического векторного потенциала.
При этом, как легко видеть из соотношений (1 – 4), магнитное и электрическое поле определятся через этот потенциал соотношениями:
(6)
Пространственная производная ![]() и локальная производная по времени
и локальная производная по времени ![]() связаны волновым уравнением (5).
связаны волновым уравнением (5).
Таким образом, использование только одного электрического векторного потенциала позволяет полностью решить задачу о распространении электрического и магнитного полей. Учитывая (6), теперь вектор Пойнтинга можно записать только через вектор ![]() :
:
Характерным является то, что при таком подходе обязательным условием распространения является наличие в данной точке пространства, как временных, так и пространственных производных одного и того же потенциала.
Данную задачу можно решить и по-другому, записав волновое уравнение для магнитного векторного потенциала:
(7)
При этом магнитное и электрическое поля будут определяться соотношениями:
Вектор Пойнтинга в данном случае может быть найден из следующего соотношения:
Пространственная производная ![]() и производная по времени
и производная по времени ![]() связаны волновым уравнением (7).
Но можно поступить и по-другому, введя, например, электрические и магнитные токи
связаны волновым уравнением (7).
Но можно поступить и по-другому, введя, например, электрические и магнитные токи
Для этих токов тоже могут быть записаны уравнения:
Эта система по своему виду и заключенной в ней информации ничем не отличается от уравнений Максвелла, и можно считать, что в пространстве распространяются магнитные или электрические токи. И решение задачи распространения при помощи данного метода опять будет содержать в себе полную информацию о процессах распространения.
Рассмотренный процесс введения новых векторных полей можно распространять в обе стороны до бесконечности, вводя все новые векторные поля. Таким образом, существует бесконечное множество возможных записей электродинамических процессов, но все они равноценны по заключенной в них информации. Такой подход был впервые продемонстрирован в работе [1].
Литература
- 1. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 2. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков,
Константа, 2003.- 72 с.
- 3. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- 4. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 5. Менде Ф. Ф. К вопросу о возникновении вторичных электрических полей при протекании через сверхпроводники постоянных токов. - Харьков, 1992.- 28 с. Рукопись депонирована в ВИНИТИ 05.11.92, № 3182-В92. Деп.
- 6. Менде Ф. Ф. К вопросу о зависимости величины заряда электронов от
скорости при протекании через сверхпроводники постоянных токов. Препринт 1–93. МГП НИИ КП при НТК ФТИНТ АН Украины, 1993 г. - 45 с.
- 7. Mende F. F. Experimental corroboration and theoretical interpretation of
dependence of charge value on DC flow velocity through superconductors. Proceedings International Conference “Physics in Ukraine”, Kiev, 1993.
- 8. Mende F. F. Conception of the scalar-vector potential in contemporary
electrodynamics, arXiv, physics/0506083.
- 9. Менде Ф. Ф. Непротиворечивая электродинамика и угроза ядерного
космического терроризма. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-9