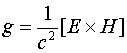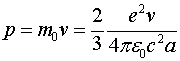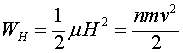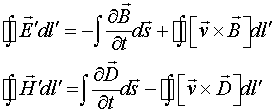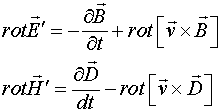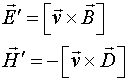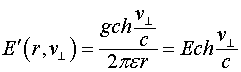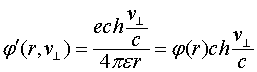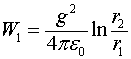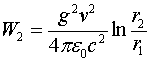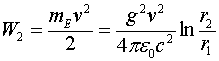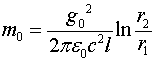Скалярно-векторный потенциал и проблема электромагнитной массы
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
В соответствии с современной концепцией электромагнетизма движущийся заряд, вместе с которым движутся его электрические поля, создаёт вокруг себя магнитное поле. Поток электрической мощности определяется при этом вектором Пойнтинга
Такое поле обладает также импульсом, плотность которого определяется соотношением [1]
(1.1)
Следует отметить, что для написания этого соотношения нет каких-то глубоких физических обоснований, а оно получено эвристическим путём, опираясь на эксперименты, которые указывают на то, что электромагнитные волны оказывают давление на те предметы, на которые они падают. В работе [1] показано, что интегрирование соотношения (1) даёт возможность получить полный импульс электрического поля движущегося заряда
(1.2)
где ![]() ,
, ![]() ,
, ![]() - заряд электрона, его скорость и радиус соответственно.
- заряд электрона, его скорость и радиус соответственно.
Из соотношения (1.2) следует, что электромагнитная масса электрона ![]() , обусловленная наличием движущихся электрических полей, определяется равенством
, обусловленная наличием движущихся электрических полей, определяется равенством
(1.3)
Недостаток такого рассмотрения заключается в том, что при движении электрона его энергетические свойства и эффективная масса зависят не только от свойств самого электрона, но и от окружающих его цепей. Приведём простой пример.
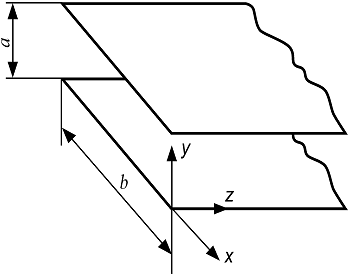
Рассмотрим двухпроводную длинную линию, состоящую из двух сверхпроводящих плоскостей (рис.1)
Рис. 1 Двухпроводная линия, состоящая из двух параллельных сверхпроводящих плоскостей
Если по проводникам такой линии течёт постоянный ток, то магнитное поле на внутренних поверхностях плоскостей, равное удельному току, можно определить из соотношения:
![]()
(1.4)
где 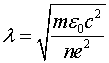 - глубина проникновения магнитного поля в сверхпроводник;
- глубина проникновения магнитного поля в сверхпроводник; ![]() ,
, ![]() - заряд и масса электрона,
- заряд и масса электрона, ![]() - плотность электронов.
Если подставить значение глубины проникновения в соотношение (1.4), то получим неожиданный результат:
- плотность электронов.
Если подставить значение глубины проникновения в соотношение (1.4), то получим неожиданный результат:
Оказывается, что величина магнитного поля вовсе не зависит от величины зарядов носителей тока, а зависит от их массы.
Таким образом, удельная энергия магнитных полей
(1.5)
в данном случае равна удельной кинетической энергия движения зарядов. Но магнитное поле, связанное с движением носителей тока в поверхностном слое сверхпроводника, существует не только на его поверхности и в скин-слое. Объём, занимаемый магнитными полями, несоизмеримо больший, чем объём скин-слоя. Если обозначить длину линии, изображённой на рис. 1, как ![]() , то объём скин-слоя в сверхпроводящих плоскостях линии составит
, то объём скин-слоя в сверхпроводящих плоскостях линии составит ![]() . Энергию магнитных полей в этом объёме определяем из соотношения:
. Энергию магнитных полей в этом объёме определяем из соотношения:
Энергия же магнитных полей, накопленная между плоскостями линии и связанная с движением зарядов в скин-слое, составит:
(1.6)
Если учесть, что глубина проникновения магнитного поля в сверхпроводниках составляет несколько сотен ангстрем, то при макроскопических размерах линии можно считать, что полную энергию магнитных полей в ней определяет соотношение (1.6).
Поэтому, образование магнитных полей ![]() между плоскостями линии, которые возникают в связи с движением зарядов в скин-слое, требует таких же затрат энергии, как если бы весь объём линии был заполнен частицами, движущимися со скоростью
между плоскостями линии, которые возникают в связи с движением зарядов в скин-слое, требует таких же затрат энергии, как если бы весь объём линии был заполнен частицами, движущимися со скоростью ![]() , плотность которых и масса составляют соответственно
, плотность которых и масса составляют соответственно ![]() и
и ![]() .
.
Очевидно, что эффективная масса электрона по сравнению с массой свободного электрона возрастает при этом в ![]() раз. Это является следствием того, что механическое движение электронов приводит не только к накоплению их кинетической энергии в скин-слое, но, ввиду зависимости их скалярного потенциала от скорости, в линии происходит также накопление потенциальной энергии, градиент которой даёт силу, действующую на проводящие плоскости линии. Таким образом, становится понятной природа таких параметров как индуктивность и эффективная масса электрона, которые в данном случае зависят, в основном, не от массы свободных электронов, а от конфигурации проводников, по которым эти электроны двигаются.
раз. Это является следствием того, что механическое движение электронов приводит не только к накоплению их кинетической энергии в скин-слое, но, ввиду зависимости их скалярного потенциала от скорости, в линии происходит также накопление потенциальной энергии, градиент которой даёт силу, действующую на проводящие плоскости линии. Таким образом, становится понятной природа таких параметров как индуктивность и эффективная масса электрона, которые в данном случае зависят, в основном, не от массы свободных электронов, а от конфигурации проводников, по которым эти электроны двигаются.
Динамические потенциалы и поля движущихся зарядов
В современной классической электродинамике отсутствуют соотношения, дающие возможность записать электрические и магнитные поля при переходе из одной инерциальной системы в другую. Такие преобразования получают, используя ковариантные преобразования Лоренца. Возникает вопрос, можно ли в классической электродинамике в рамках преобразований Галилея получить такие преобразования. Указанные преобразования можно получить, если записать законы индукции, используя полные производные полей. Такой подход физически понятен, т.к. производные полей по времени можно получить не только за счёт частных производных по этому параметру, но и за счёт движения в пространственно меняющихся полях.
Как показано в работах [2-6] законы индукции, записанные в полных производных имеют симметричный вид:
(2.1)
или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [2]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [2]. Электрическое поле 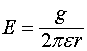 за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [2-6]:
(2.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
Электромагнитная масса полей движущихся зарядов в концепции скалярно-векторного потенциала
Принято считать, что кинетическая энергия электронов и других заряженных частиц определяется той разностью потенциалов ![]() , при помощи которой эти частицы были ускорены.
, при помощи которой эти частицы были ускорены.
Но в случае электронного пучка всегда имеется замкнутая цепь, по которой электроны возвращаются обратно к источнику питания. С другой стороны, вокруг электронного потока всегда имеется радиальное электрическое поле, которое исчезает при попадании пучка в мишень. Это поле тоже имеет энергию, которая должна выделяться в таком процессе. Поэтому возникает два вопроса. Влияют ли внешние цепи, как в случае со сверхпроводящей линией, на эффективную массу электронов и имеют ли какое-то отношение электрические поля, окружающие электронный поток, к наблюдаемой массе электронов.
Рассмотрим проводящую трубу, имеющую заглушку с одной стороны, по оси которой движется электронный поток (рис. 2). Электронный поток ускоряется разностью потенциалов между катодом и анодом. Внутри трубы поток движется с постоянной скоростью.
Рис. 2. Электронный поток внутри пустотелого анода.
Если на единицу длины электронного потока, движущегося внутри пустотелого анода, приходится заряд ![]() , то скалярный потенциал пучка, с учётом его зависимости от скорости, запишется
, то скалярный потенциал пучка, с учётом его зависимости от скорости, запишется
где ![]() - скорость зарядов в пучке.
- скорость зарядов в пучке.
Учитывая только два первых члена разложения гиперболического косинуса в ряд, находим электрическое поле пучка:
(3.1)
Учитывая, что удельная энергия электрического поля определяется соотношением
(3.2)
можно найти энергию электрических полей, приходящуюся на единицу длины электронного пучка. В цилиндрической системе координат элемент объёма единичной длины составляет
(3.3)
Учитывая (3.1 – 3.3), находим энергию электрического поля, приходящуюся на элемент объёма ![]()
(3.4)
Для нахождения энергии пучка, приходящуюся на единицу его длины, проинтегрируем (3.4) по радиусу и углу, пренебрегая членом ![]() :
:
(3.5)
В этом соотношении ![]() - радиус электронного пучка, а
- радиус электронного пучка, а ![]() - внутренний радиус трубы. Видно, что энергия, хотя и слабо, зависит от отношения радиусов. Поэтому с практической точки зрения для получения максимальной энергии пучка следует брать это отношение максимальным.
- внутренний радиус трубы. Видно, что энергия, хотя и слабо, зависит от отношения радиусов. Поэтому с практической точки зрения для получения максимальной энергии пучка следует брать это отношение максимальным.
Из соотношения (3.5) видно, что энергия электрического поля электронного пучка состоит из двух частей. Первая из них характеризует поле неподвижного потока и от скорости не зависит
Вторая часть, как и кинетическая энергия, имеет квадратичную зависимость от скорости
Она и даёт кинетическую энергию заряда, которая может быть охарактеризована электромагнитной массой, связанной с наличием радиальных электрических полей заряда, зависящих от скорости:
Откуда получаем:
(3.6)
В данном соотношении ![]() это величина электрической массы, приходящаяся на единицу длины
это величина электрической массы, приходящаяся на единицу длины ![]() , а
, а ![]() - величина заряда, приходящегося на ту же длину. Введя обозначения
- величина заряда, приходящегося на ту же длину. Введя обозначения 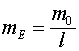 и
и  , где
, где ![]() и
и ![]() - масса и заряд единицы длины, перепишем соотношение (3.6):
- масса и заряд единицы длины, перепишем соотношение (3.6):
Сравнивая (3.6) и (1.3) легко видеть, что структура этих соотношений одинакова и электрические поля электрического пучка имеют массу электрического происхождения. Однако получили мы это соотношение, не вводя ни вектора Пойнтинга, ни магнитного поля, а воспользовавшись концепцией зависимости скалярного потенциала заряда от его относительной скорости.
Список литературы
- 1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, том 6 Электродинамика, М: Мир, 1977.
- 2. Менде Ф. Ф. К вопросу о возникновении вторичных электрических полей при протекании через сверхпроводники постоянных токов. - Харьков, 1992.- 28 с. Рукопись депонирована в ВИНИТИ 05.11.92, № 3182-В92. Деп.
- 3. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с.
- 4. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- 5. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 6. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.