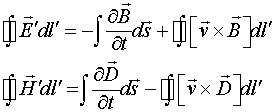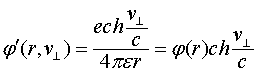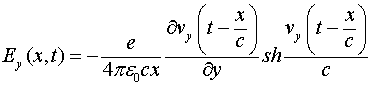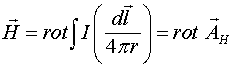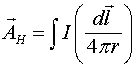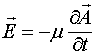Скалярно-векторный потенциал и проблема излучения
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
Одним из самых загадочных процессов в электродинамике является излучение электромагнитных волн. Очень странным обстоятельством является то, что электромагнитную волну заряд излучает не в направлении своего движения, а в направлении нормальном к такому движению. Это обстоятельство и рассматривается сторонниками эфирных теорий как доказательство существования эфира. Сам заряд имеет силовые линии электрического поля, расходящиеся радиально от него, тем более напряженность таких полей обратно пропорциональна квадрату расстояния, в то время как электрические поля излучения направлены нормально к электрическим полям самого заряда и убывают обратно пропорционально расстоянию, т.е. гораздо медленнее, чем электрические поля самого заряда.
Концепция скалярно-векторного потенциала и здесь даёт ясную физическую картину происходящего.
Динамические потенциалы и поля движущихся зарядов
Тот путь, который будет продемонстрирован в этой статье, касающийся введения в законах индукции полных производных полей, прошел в значительной части в своё время ещё Герц. Правда, он не вводил понятие векторных потенциалов, а оперировал только полями, но это не умаляет его заслуг. Герц ошибался лишь в том, что считал электрические и магнитные поля инвариантами скорости.
Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами, а также электромагнитными волнами, которые генерируются неподвижными и движущимися источниками таких волн. Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
Как уже отмечалось, в классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной [1].
В данном статье будет сделана попытка найти физически обоснованные причин силового взаимодействия токонесущих систем. Первый шаг, продемонстрированный в работах [2-5], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы записываются следующим образом:
(1.1)
или
(1.2)
Для постоянных полей эти соотношения имеют вид:
(1.3)
В соотношениях (1.1-1.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (1.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (1.1), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (1.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле  за пределами заряженного длинного стержня, на единицу длины которого приходится заряд g, убывает по закону
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд g, убывает по закону ![]() , где r - расстояние от центральной оси стержня до точки наблюдения.
, где r - расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле E начать двигать со скоростью Δv другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью Δv, то уже за счет движения в поле ΔH появится добавка к электрическому полю
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью Δv, то уже за счет движения в поле ΔH появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда e, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [1-4]:
(1.4)
где φ(r) - скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда.
Законы электро-электрической индукции
Поскольку любой процесс распространения электрических полей и потенциалов всегда связан с запаздыванием, введём запаздывающий скалярно-векторный потенциал, считая, что поле этого потенциала распространяется в данной среде со скоростью света:
(2.1)
где  – составляющая скорости заряда g, нормальная к вектору
– составляющая скорости заряда g, нормальная к вектору ![]() в момент времени
в момент времени  , r – расстояния между зарядом и точкой, в которой определяется поле, в момент времени t.
, r – расстояния между зарядом и точкой, в которой определяется поле, в момент времени t.
Используя соотношение ![]() , найдём поле в точке 1 (рис. 1) .
, найдём поле в точке 1 (рис. 1) .
Рис. 1. Схема формирования индуцированного электрического поля.
Градиент числового значения радиуса вектора ![]() есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси x и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая: 1) точка истока фиксирована и
есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси x и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая: 1) точка истока фиксирована и ![]() рассматривается как функция положения точки наблюдения; и 2) точка наблюдения фиксирована и
рассматривается как функция положения точки наблюдения; и 2) точка наблюдения фиксирована и ![]() рассматривается как функция положения точки истока.
рассматривается как функция положения точки истока.
Будем считать, что заряд e совершает колебательное движение вдоль оси y, в окрестности точки 0, которая является точкой наблюдения, а точкой истока является фиксированная точка 1 и ![]() рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
При условии, что амплитуда колебаний заряда значительно меньше, чем расстояние до точки наблюдения, можно считать радиус вектор постоянная величина. При этом условии получаем:
(2.2)
где x - какая-то фиксированная точка на оси x.
Учитывая, что
из (2.2) получаем:
(2.3)
Это и есть полный закон излучения движущегося заряда.
Если взять только первый член разложения  , то из (2.3) получим
, то из (2.3) получим
(2.4)
где  - запаздывающее ускорение заряда.
- запаздывающее ускорение заряда.
Это соотношение является волновым уравнением и определяет как амплитудные, так и фазовые характеристики волны электрического поля, излучаемого движущимся зарядом.
Если в качестве направления излучения взять вектор, лежащий в плоскости xy, и составляющий с осью y угол α, то соотношение (2.4) принимает вид:
(2.5)
Соотношение (2.5) определяет диаграмму направленности излучения. Поскольку в данном случае есть осевая симметрия относительно оси y , то можно вычислить полную диаграмму направленности рассмотренного излучателя. Эта диаграмма соответствует диаграмме направленности дипольного излучателя.
Поскольку  - запаздывающий векторный потенциал, то соотношение (2.5) можно переписать
- запаздывающий векторный потенциал, то соотношение (2.5) можно переписать
Опять получено полное совпадение с уравнениями запаздывающего векторного потенциала в классической электродинамики, но векторный потенциал введён здесь не эвристическим феноменологическим способом, а с использованием понятия запаздывающего скалярно-векторного потенциала. Нужно отметить одно важное обстоятельство: в уравнениях Максвелла электрические поля, представляющие волну, вихревые. В данном же случае электрические поля носят градиентный характер.
Продемонстрируем ещё одну возможность, которую открывает соотношение (2.5). Известно, что в электродинамике существует такое понятие, как электрический диполь и дипольное излучение, когда заряды, колеблющиеся в электрическом диполе, излучают электромагнитные волны. Два заряда с противоположными знаками имеют дипольный момент:
(2.6)
где вектор ![]() направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
Следовательно
и
Подставляя данное соотношение в выражение (2.5), получаем закон излучения колеблющегося диполя.
(2.7)
Это также очень хорошо известное соотношение [7].
Таким образом, в процессе колебания электрического диполя создаются электрические поля двух видов. Во-первых, это электрические индукционные поля излучения, представляемые соотношениями (2.4), (2.5) и (2.6), связанные с ускорением заряда. С другой стороны, вокруг колеблющегося диполя образуются электрические поля статического диполя, которые изменяются во времени в связи с тем, что расстояние между зарядами зависит от времени. Суммарное же значение поля, вокруг такого диполя определяют как суперпозицию полученных полей.
Законы (2.4), (2.5), (2.7) - это законы прямого действия, в которых уже нет ни магнитных полей, ни векторных потенциалов. Т.е. те строительные леса, которыми являлись магнитное поле и магнитный векторный потенциал уже сняты и они нам больше не нужны.
Используя соотношение (2.5) можно получить законы отражения и рассеивания как для одиночных зарядов, так и, для любого их количества. Если какой-либо заряд или группа зарядов подвергаются действию внешнего (стороннего) электрического поля, то такие заряды начинают осуществлять вынужденное движение, и каждый из них излучает электрические поля в соответствии с соотношением (2.5). Суперпозиция электрических полей, излучаемых всеми зарядами, является электрической волной.
Если на заряд действует стороннее электрическое поле ![]() , то ускорение заряда определяют как:
, то ускорение заряда определяют как:
С учётом этого соотношение (2.7) принимает вид
(2.8)
где коэффициент 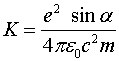 может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
Волне электрического поля (2.5) сопутствует волна тока смещения:
Если заряд осуществляет своё движение под воздействием стороннего электрического поля ![]() , то ток смещения в дальней зоне записывают:
, то ток смещения в дальней зоне записывают:
(2.9)
Суммарная волна, которая представляет распространение электрических полей (2.8) и токов смещения (2.9), может быть названа электротоковой. В этой волне ток смещения отстаёт от волны электрического поля на ![]() . Впервые этот термин и определение такой волны было дано в работе [2].
. Впервые этот термин и определение такой волны было дано в работе [2].
Параллельно с электрическими волнами можно ввести магнитные волны, если положить, что
Введённое таким образом магнитное поле является вихревым. Сравнивая (2.9) и (2.10) получаем:
Интегрируя это соотношение по координате, находим значение магнитного поля
(2.11)
Таким образом, соотношения (2.8), (2.9) и (2.11) могут быть названы законами электро-электрической индукции, т.к. дают непосредственную связь между прикладываемыми к заряду сторонними электрическими полями и полями индуцируемыми этим зарядом в его окрестности. Сам же заряд выступает в данном случае в роли своеобразного трансформатора, обеспечивающего такое преизлучение.
Магнитное поле, которое можно вычислить при помощи соотношения (2.11), направлено нормально и к электрическому полю и к направлению распространения, а их отношение в каждой точке пространства составляет:
где Z - волновое сопротивление свободного пространства.
Волновое сопротивление определяет активную мощность потерь на единичной площадке, расположенной нормально к направлению распространения волны:
Поэтому электротоковая волна, пересекая такую площадку, переносит через неё мощность, определяемую данным соотношением, что находится в согласии с теоремой Пойнтинга о потоке мощности электромагнитной волны. Поэтому, для нахождения всех параметров, характеризующих волновой процесс, распространения и переноса энергии посредством полей, достаточно рассмотрения лишь электротоковой волны и знания волнового сопротивления пространства. При этом совсем не обязательно вводить такое понятие, как «магнитное поле» и его векторный потенциал, хотя ничего незаконного в этом нет. В такой постановке соотношения, полученные для электрического и магнитного поля, полностью удовлетворяют теореме Гельмгольца. Эта теорема гласит, что всякое однозначное и непрерывное векторное поле ![]() , обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции
, обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции ![]() и ротора некоторой векторной функции
и ротора некоторой векторной функции ![]() , дивергенция которой равна нулю:
, дивергенция которой равна нулю:
Следовательно, должно существовать чёткое разделение полей на градиентные и вихревые. Видно, что в полученных выражениях для индуцируемых полей такое разделение имеется. Электрические поля носят градиентный характер, а магнитные – вихревой.
Таким образом, построение электродинамики нужно было начинать с признания зависимости скалярного потенциала от скорости, как это предлагал Вебер. Но в том-то и дело, что природа очень глубоко прячет свои секреты, и, чтобы прийти к такому простому выводу, пришлось пройти путь длиной почти в два столетия. Металлические опилки, которые так дружно выстраивались вокруг полюсов магнита, прямым образом указывали на наличие каких-то силовых полей потенциального характера, но на это не обратили внимания, поэтому и оказалось, что все разглядели только верхушку айсберга, значительная часть которого оставалась невидимой почти двести лет.
С учётом всего сказанного следует полагать, что в основе подавляющего большинства статических и динамических явлений в электродинамике лежит одна единственная формула (2.1), предполагающая зависимость скалярного потенциала заряда от скорости его движения. Из неё следует и статическое взаимодействие зарядов, и законы силового взаимодействия в случае их взаимного движения, и законы излучения и рассеивания. Такой подход позволил объяснить с позиций классической электродинамики следующие явления: фазовая аберрация и поперечный эффект Доплера, которые в рамках существующей классической электродинамики объяснения не находили. После всего сказанного можно снять строительные леса, такие как магнитное поле и магнитный векторный потенциал, которые не позволяют вот уже почти двести лет увидеть здание электродинамики во всём его величии и красоте.
Заметим, однако, что одно из основных уравнений индукции (2.4) можно было получить прямо из закона Ампера, ещё задолго до того, как появились уравнения Максвелла. Закон Ампера, выраженный в векторной форме, определяет магнитное поле в точке x,y,z в следующем виде:
где I - ток в элементе ![]() ,
, ![]() - вектор, направленный из
- вектор, направленный из ![]() в точку x,y,z.
в точку x,y,z.
Можно показать, что
и, кроме того, что
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
где
(2.12)
Замечательным свойством этого выражения является то, что векторный потенциал зависит от расстояния до точки наблюдения как ![]() . Именно это свойство и позволяет получить законы излучения.
. Именно это свойство и позволяет получить законы излучения.
Поскольку ![]() , где g количество зарядов, приходящееся на единицу длины проводника, из (21.12) получаем:
, где g количество зарядов, приходящееся на единицу длины проводника, из (21.12) получаем:
Для одиночного заряда e это соотношение принимает вид:
а поскольку
то
(2.13)
Для одиночного заряда это соотношение выглядит следующим образом:
(2.14)
Если в соотношениях (2.13) и (2.14) учесть, что потенциалы распространяются с конечной скоростью и учесть запаздывание  , и с учётом, что для вакуума
, и с учётом, что для вакуума 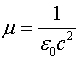 , эти соотношения примут вид:
, эти соотношения примут вид:
(2.15)
(2.16)
Соотношения (2.15) и (2.16) представляют, как показано выше (см. (2.4), волновые уравнения. Отметим, что эти уравнения - это решение уравнений Максвелла, но в данном случае они получены непосредственно из закона Ампера, вообще не прибегая к уравнениям Максвелла. Остаётся только задать вопрос, почему электродинамика в своё время не пошла этим путём?
Литература
- 1. Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967, - 664 – с.
- 2. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с. ISBN – 966-7983-55-2.
- 3. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 4. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- 5. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.
- 6. 14. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 7. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.