Попов А.И: Измерение скорости ракеты к моменту отделения первой ступени
| 1. Краткая история американской лунной ракеты | 4. Операция «Кроссроуд»: охрана призрака |
| 2. Измерение скорости ракеты на 110-112с полёта | 5. 1970 год: находка в Атлантике |
| 3. Измерение скорости ракеты к моменту отделения первой ступени | 6. Ракета «Сатурн-5» - «не более чем миф» |
Как сказано выше, возможность точно измерить скорость ракеты мы получили благодаря кинохронике NASA. Речь идет примерно о 160-й секунде полёта, - за 2-3с до того, как, по расписанию NASA, от ракеты отделяется первая ступень.
Почитаем описание этого отрезка полёта в воспоминаниях ветерана советской космонавтики академика РАН Б.Е. Чертока:[1] «21 декабря 1968 года, суббота, хорошая погода, но праздничного настроения не было. В НИИ-88 мы любовались стартом «Сатурна-5» с «Аполлоном-8». Старт даже на телевизионном экране возбуждал чувства восхищения... При разделении первой и второй ступеней все окутывается выплесками дыма и пламени. Создается впечатление, что произошел взрыв, — но через секунды яркий чистый факел устремляется дальше».
Посмотрим, как всё это выглядит по кинохронике NASA на примере 30-секундного клипа NASA[2] о полёте «лунной» ракеты А-11 (илл.1). Мы полагаем, что принципиальная схема полёта «Сатурнов-Аполлонов» (в данном случае А-8 и А-11) на стадии запуска была в главных чертах одинакова. Клип включает в себя несколько секунд полёта ракеты до «взрыва», сам «взрыв» и примерно 20 секунд после него.

На самом деле, как показывает покадровый анализ кинохроники NASA, этот странный «взрыв» происходит не в момент отделения первой ступени (как о том пишет Б. Черток), а примерно за 3с до этого. В этой главе мы не будем вдаваться в причины этого «взрыва». Нам важно то, что, благодаря именно этому «взрыву», мы получили возможность в указанный момент времени измерить скорость ракеты относительно окружающего воздуха. По американским данным[3] ракета перед отделением первой ступени достигает скорости
 NASA = 2, 4 км/с относительно окружающего воздуха (1)
NASA = 2, 4 км/с относительно окружающего воздуха (1)
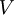 NASA = 2, 4 км/с относительно окружающего воздуха (1)
NASA = 2, 4 км/с относительно окружающего воздуха (1)
Он показал, что ракеты летит примерно в 2 раза медленнее и сделал вывод, что такая медленная ракета не могла достичь Луны.[6][7][8][9] Аналогичные результаты получены авторами.[10][11] Работы[6][7][8][9][10] подверглись критике со стороны защитников NASA.[12] Поскольку полемика интересует достаточно узкий круг читателей, то она отнесена в приложение 2, а здесь мы познакомимся с тремя методами измерения скорости ракеты в момент «взрыва» и сразу после него.
Содержание
1. Метод «по конусу Маха»
Конус Маха. Читатель, незнакомый с этим понятием, легко поймёт сущность этого физического явления, если посмотрит на картину мчащегося катера (илл.2). Если его скорость больше скорости распространения волн на воде, то за ним образуется характерный треугольный шлейф из отбрасываемой в стороны воды.
Примерно то же самое происходит и в воздухе, если через него летит объект (самолёт, ракета) со скоростью, превышающёй скорость звука, то есть, скорость волн плотности в воздухе. За таким объектом образуется след с границей из отброшенного уплотнённого воздуха. Только след не треугольный, а конический, потому что явление происходит не на плоскости, как в случае с катером, а в объёме. Он и называется конусом Маха. Чем быстрее мчится катер, тем острее будет треугольный след за ним. Точно так же, чем быстрее летит ракета, тем острее будет угол конуса Маха. По величине этого угла можно определить скорость ракеты относительно воздуха.
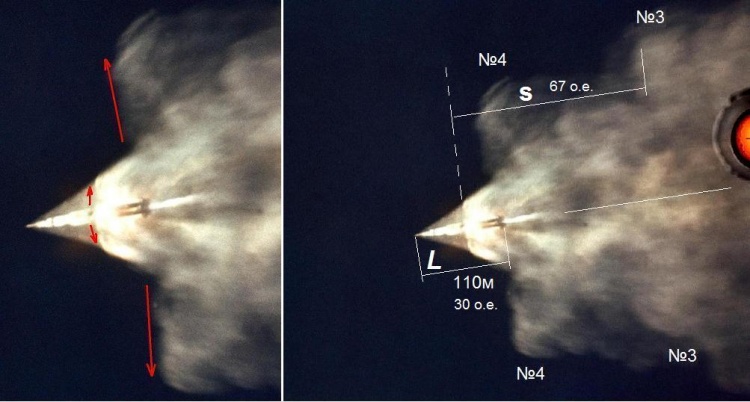
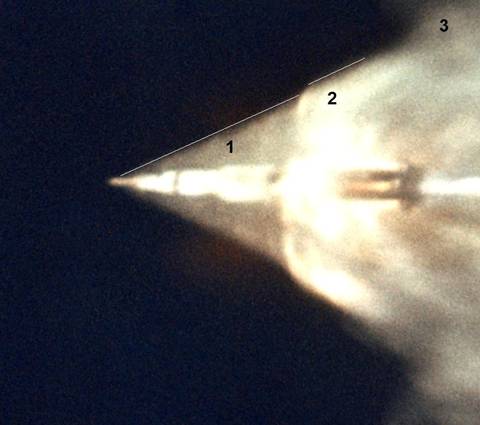
На илл.3 показан уникальный снимок американской «лунной» ракеты, снятый за несколько секунд до отделения первой ступени. Он сделан с наблюдательного самолёта NASA (ALOTS)[13][14][15][16][17][18][19][20] и отличается значительно более высоким качеством по сравнению с другими фото-киноматериалами NASA на ту тему.
Эффектный конус, обрамляющий ракету, и есть конус Маха. Граница конуса является ударной волной, на фронте которой плотность воздуха резко возрастает. Нам повезло, что конус Маха виден, поскольку обычно воздух вокруг ракеты прозрачен. Но на илл.3 ракета снята в очень необычный момент, когда она окружена облаком от некоего «взрыва» - того самого, о котором писал Б.Е. Черток. Не будем отвлекаться и рассуждать о причине этого «взрыва». Нам важно лишь то, что частицы дыма рассеивают солнечные лучи и делают конус видимым. При этом дым не может проникнуть через барьер скачка плотности наружу и покинуть конус Маха. Тем самым освещённый дым прекрасно очерчивает конус.

 при вершине конуса определяется простой формулой:[22][23]
при вершине конуса определяется простой формулой:[22][23]
 (2)
(2)
где 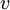 — скорость ракеты,
— скорость ракеты,  — скорость звука в среде, величина
— скорость звука в среде, величина  называется числом Маха и часто используется ниже.
называется числом Маха и часто используется ниже.
Легко измерить этот угол. И, казалось бы, ничто не мешает нам определить величину М. Однако формула (2) справедлива, если вектор скорости ракеты перпендикулярен лучу зрения снимающей камеры. Если же угол этот угол не прямой (например, самолёт «смотрит» вдогонку ракете), то конус Маха будет казаться менее острым, чем он есть на самом деле. В приложении 1 показано, как учитывается это искажение. А здесь мы сразу даём соответствующий результат: при рассмотрении конуса Маха ракеты под прямым углом он выглядел бы так, как показано на илл.4.
Измеряя катет и гипотенузу прямоугольного треугольника на илл.4, находим  = 0,33, откуда по формуле (2) вычисляем:
= 0,33, откуда по формуле (2) вычисляем:
 или
или 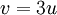 (3)
(3)
Остаётся подставить в (3) значение скорости звука на высоте отделения первой ступени. Скорость звука не так уж сильно зависит от высоты. Так, согласно[24] в диапазоне высот от 0 до 80 км она изменяется примерно на10%. Тем не менее, попробуем учесть и эту зависимость. Для этого нужно уточнить значение высоты, на которой происходит отделение первой ступени. Согласно NASA отделение это происходит на высоте 66 км.[3] Но после знакомства с результатами предыдущей главы у нас нет основания доверять эти данным. Ракета, которая начала свой полёт со скоростью в 2-3 раза медленнее, чем это необходимо по графику самого NASA, не может достичь такой высоты. Логично считать, что и высота отделения первой ступени будет, по крайней мере, в 2-3 раза меньше. То есть – примерно 20-30км. Это подтверждается и независимой оценкой, сделанной автором[25] на основе изучения совершенно других физических факторов. Скорость звука на высотах 20-30км составляет около 300м/с.[24] Этому значению скорости соответствует:
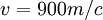 (4)
(4)
2. Метод «по отставанию дымов»
На илл.5 показаны без перерыва 12 кадров клипа[2] от момента 8,96с до момента 9,42с (общее время ~ 0,45с). Обратите внимание на форму одного из выбросов дыма. Он отмечен цветными точками. На первых двух кадрах (красные точки) его форма заметно меняется, следовательно, он находится в движении. На третьем кадре (9,04с) изменения формы уже мало заметны, а начиная примерно с кадра (9,08с), форма практически стабилизируется. Трудно представить, что дымовое облако может мчаться за ракетой, преодолевая сопротивление воздуха, но сохраняя при этом форму. Это говорит о том, что, начиная с кадра «9,08с» облако можно считать практически неподвижным по сравнению с быстрым перемещением ракеты. Поэтому относительно него можно измерять продвижение ракеты.
Для этого достаточно сравнить всего два кадра с остановившимися дымами из серии илл.5 - первый (9,08с) и последний (9,42с), где отмеченный клуб дыма ещё попадает в поле зрения. Эти кадры обведены на илл.5 синими рамками. На илл.6 для удобства сравнения они показаны рядом и в увеличенном масштабе. Здесь приведены значения нескольких размеров в относительных единицах (о.е) и размер ракеты в м. Ракета на кадре (9,42с) видна с разрешением, которое оставляет желать лучшего. Поэтому требуется пояснить, и как определён её относительный размер (27 о.е.) и почему её абсолютный размер на данном кадре указан, как 105м, хотя известно, что полная длина ракеты от хвоста до кончика передней иглы составляет 110м.
Обратимся за помощью опять к единственному кадру приличного разрешения (илл.3), но посмотрим его с увеличением. Это сделано на илл.7. Сопоставление формы дымового облака вокруг ракеты на илл.5 (9,04с) и на илл.7 показывает, что хорошее изображение со всей очевидностью изъято из той же самой киноплёнки, из которой вырезан изучаемый клип. Зачем NASA ухудшила качество изображения, представляя клип,[2] мы здесь обсуждать не будем.Границу ракеты справа на илл.7 достаточно точно обозначает начало ровной струи газов, вырывающихся из хвостовой части. По аналогии именно так указана правая граница ракеты на илл.6.
Граница ракеты слева на илл.7 тоже очевидна. Это остриё иглы САС ракеты (САС – система аварийного спасения). А вот на илл.6 из-за плохого качества кадра мы не можем быть уверены в том, что мы видим слева. Ведь игла САС на илл.6 неразличима. Во что трансформировалось её изображение вследствие плохого разрешения? Или она просто не видна, и тогда видимый размер ракеты следует принять не 110м, а 100м – то есть короче на длину этой иглы. Или она слилась с ракетой в общий контур, и тогда видимый размер ракеты остаётся равным 110м. Автор выбрал «золотую» середину и принял видимый размер ракеты на илл.6 равным 105м. Отметим, что в таком случае принимаемая видимая длина ракеты отличается всего на ±5% от обоих названных случаев.
Тогда получается, что ракета пролетела расстояние  . Это произошло за время 0,34с. Отсюда второй метод даёт следующее значение для скорости ракеты относительно окружающего её воздуха:
. Это произошло за время 0,34с. Отсюда второй метод даёт следующее значение для скорости ракеты относительно окружающего её воздуха:
 (5)
(5)
3. Метод «по боковым выбросам взрывных продуктов»
В качестве третьего метода определения v автор данной статьи использовал наблюдения за теми выбросами продуктов упомянутого «взрыва», которые происходят перпендикулярно направлению полёта ракеты. Сначала разберём идею метода на простом примере (илл.8).
Вот летит боевой вертолёт и для своей защиты от зенитных самонаводящихся ракет через определённые промежутки времени 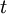 пускает вправо и влево тепловые ракеты. Скажем, сначала он выпустил ракету 1, а через время
пускает вправо и влево тепловые ракеты. Скажем, сначала он выпустил ракету 1, а через время 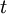 - ракету 2. Обе тепловые ракеты оставили белые следы. Расстояние s между этими следами можно определить, если известна длина
- ракету 2. Обе тепловые ракеты оставили белые следы. Расстояние s между этими следами можно определить, если известна длина 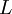 вертолёта. И если мы смогли засечь промежуток времени
вертолёта. И если мы смогли засечь промежуток времени 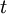 , то ничто не мешает определить скорость полёта вертолёта, как
, то ничто не мешает определить скорость полёта вертолёта, как  .
.
Оказывается, что в момент «взрыва» вокруг лунной ракеты справа и слева от неё образуются боковые дымовые выбросы, причём они выбрасываются с некоей периодичностью. Чтобы увидеть эти выбросы вновь обратимся к клипу.[2] В предыдущем разделе изучен выход ракеты из дымового облака и удаление от него. Теперь мы вернёмся на секунду раньше и посмотрим «взрыв» от его начала и до конца (илл.9,10). На илл.6 слева ракета показана за ~0,3с до «взрыва» (точное время на этом кадре не так уж важно). На следующих четырёх кадрах видно, как за 0,16с облако «взрыва» закрыло практически всю ракету. Это первая вспышка «взрыва».
Последний кадр из илл.9 (8,08с) открывает следующую последовательность кадров (илл.10). Через 0,12с облако, лишённое поступлений новых порций вещества теряет резкие черты (8,20с). Ещё через 0,14с заметны новые выбросы вещества (8,34с). Это - вторая вспышка. И вновь облако «оплывает», лишённое свежей «подпитки» (8,48с). Ещё через 0,14с следует третья вспышка (8,62с). Последней будет четвёртая вспышка (8,88с). Одинаковые характерные фазы, определяемые по виду передней части облака, отмечены на илл.10 белой рамкой вокруг отметки времени. Временной интервал между вспышками составляет 0,26?0,28с. После четвёртой вспышки облако, лишённое новых порций вещества, тормозится набегающим потоком воздуха и перестаёт следовать за ракетой. Из него показывается голова ракеты (9,04с), вокруг которой образуется уже знакомый нам конус Маха.
Но где же те боковые выбросы, которые так необходимы для реализации идеи метода? На илл.9,10 их не увидишь: слишком плохое у них качество. Они сослужили свою службу тем, что показали, что во время взрыва дымы выбрасываются через примерно равные промежутки времени (~1/4с), как те тепловые ракеты, что показаны на илл.8. Но, чтобы разглядеть, в каком преимущественном направлении выбрасываются дымы при «взрыве», нужно лучшее качество изображения. Эту возможность нам предоставляет всё тот же уникальный кадр с хорошим разрешением. На илл.11 показаны те его фрагменты, которые интересны для реализации третьего метода.
На левом фрагменте мы видим, что продукты сгорания взрыва в виде ярких белых струй вырываются перпендикулярно корпусу ракеты, то есть вбок. Характерные боковые рукава из дыма, напоминающие мохнатые лапы плюшевой игрушки, это тоже выбросы продуктов сгорания, но выброшенные на несколько мгновений раньше. Они тоже имеют преимущественное направление вбок. Их разделяет тёмная «талия» провала в дымах. Она соответствует минимуму взрывной активности между двумя вспышками.
Первый рукав по ходу ракеты – от вспышки №4, предыдущий – от вспышки №3. Вспышка №3 уже закончилась. Вспышка №4 произошла только что и ещё не закончилась. Она ещё горит в средней части ракеты, образуя яркую белую юбочку из продуктов горения. Но эти остатки продуктов горения уже не вырвутся наружу. Сила напора их недостаточна и они зажаты набегающим воздухом, формирующим в данный момент конус Маха. Продолжим штриховой линией начальное направление движения этих остаточных продуктов, что понять, где была бы граница выброса №4, если бы ему не мешали тиски конуса Маха.
Пользуясь длиной ракеты (110м), как масштабом, находим расстояние между боковыми выбросами №3 и №4 s ~ 245м. Временной интервал между вспышками №3 и №4 известен - 0,26с (илл.13). Деля 245м на 0,26 сек, получаем скорость «лунной» ракеты относительно окружающего её воздуха:
 (6)
(6)
4. Усреднение по трём методам
В данной статье тремя различными методами определены три значения (4,5,6) для скорости «лунной» ракеты в момент, предшествующий разделению первой и второй ступеней. Каждый из этих методов имеет свои достоинства и недостатки. Учитывая это, автор умышленно не привёл погрешности значений скорости ракеты 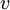 , найденных по каждому отдельно взятому методу. Ошибку определим после усреднения по всем трём методам. Это усреднение даёт следующий конечный результат:
, найденных по каждому отдельно взятому методу. Ошибку определим после усреднения по всем трём методам. Это усреднение даёт следующий конечный результат:
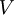 изм = (960 ± 50) м/с (7)
изм = (960 ± 50) м/с (7)
Это в 2,5 раза меньше того, что сообщает NASA. Весьма малая погрешность среднего показывает на то, что методы взаимно подтвердили друг друга. Так что результатом наших измерений явилась не оценка значения скорости «лунной» ракеты, как это часто пытаются представить защитники NASA, а её весьма точное измерение ( ±5%).
С.Г. Покровский в своих работах[6][7][8][9] даёт 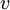 =1,2 км/с, то есть на 20% больше, чем значение (7). На самом деле, соответствие результатов данной статьи и,[6][7][8][9] по-видимому, ещё лучше. Дело в том, что Покровский принял для расчёта сильно завышенное значение скорости звука
=1,2 км/с, то есть на 20% больше, чем значение (7). На самом деле, соответствие результатов данной статьи и,[6][7][8][9] по-видимому, ещё лучше. Дело в том, что Покровский принял для расчёта сильно завышенное значение скорости звука 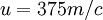 . Если результат Покровского пересчитать к скорости звука 300м/с, то получится как раз значение (7).
. Если результат Покровского пересчитать к скорости звука 300м/с, то получится как раз значение (7).
Куда летели эти ракеты?
Итак, ракета действительно летит в 2,5 раза медленнее и на значительно меньшей высоте, чем о том говорит NASA. Полагая, что ракета движется приблизительно равноускоренно, можно показать, что достигаемая высота примерно пропорциональна достигаемой скорости. Это означает, что высота, на которой происходит «взрыв» (и следующее за ним отделение первой ступени) в 2,5 раза меньше той, что указывает NASA (66 км). То есть истинная высота описываемого события примерно равна всего лишь 25 км. Следует отметить, что ко времени написания настоящей главы появились и более жёсткие оценки по высоте полёта ракеты. То есть высота полёта ракеты ещё ниже.[26] Автор оставляет их за скобками рассмотрения только по одной причине: пусть эти новые данные «устоятся» и пройдут через критическое обсуждение. Хотя очень возможно, что они более правильны. Время покажет. Но и без учёта этих новых результатов весьма сомнительно, что путь такой ракеты лежит на Луну. Чтобы показать это, достаточно напомнить, что кинетическая энергия движущегося тела определяется известной школьной формулой  . И если реальная скорость ракеты к моменту отделения первой ступени в 2,4 раза меньше официального значения, то её кинетическая энергия будет в 5,5 раз меньше. То есть ракета набрала менее 20% от кинетической энергии, необходимой для осуществления реального полёта. Какая уж тут Луна! Поэтому, начиная с этого момента, мы слова лунная ракета будем писать только с использованием кавычек. Спорный вопрос, могла ли такая ракета выйти даже на околоземную орбиту. Скорее всего, конец её пути гораздо ближе – в водах Атлантического океана. А кому захочется закончить свой жизненный путь полётом на ракете-макете в воды Атлантики? Так что наиболее вероятно, что стартовавшая ракета-макет падала в Атлантику и была беспилотной. Так что американцам было, что скрывать об этой ракете. И они это делали. Об этом рассказано в следующей главе.
. И если реальная скорость ракеты к моменту отделения первой ступени в 2,4 раза меньше официального значения, то её кинетическая энергия будет в 5,5 раз меньше. То есть ракета набрала менее 20% от кинетической энергии, необходимой для осуществления реального полёта. Какая уж тут Луна! Поэтому, начиная с этого момента, мы слова лунная ракета будем писать только с использованием кавычек. Спорный вопрос, могла ли такая ракета выйти даже на околоземную орбиту. Скорее всего, конец её пути гораздо ближе – в водах Атлантического океана. А кому захочется закончить свой жизненный путь полётом на ракете-макете в воды Атлантики? Так что наиболее вероятно, что стартовавшая ракета-макет падала в Атлантику и была беспилотной. Так что американцам было, что скрывать об этой ракете. И они это делали. Об этом рассказано в следующей главе.
Приложение 1.
Восстановление истинного угла  при вершине конуса Маха для случая, когда ракета летит под косым углом к лучу зрения камеры
при вершине конуса Маха для случая, когда ракета летит под косым углом к лучу зрения камеры
Снимок илл.3а сделан с самолёта, показанного на илл.12.[13][14][15][16][17][18][19][20] На схеме илл.12 показан общий случай, когда угол между вектором скорости ракеты и лучом зрения камеры отличается от прямого на некоторый угол  . Истинные значения длины ракеты и её скорости обозначены как
. Истинные значения длины ракеты и её скорости обозначены как 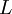 и
и 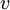 . Наблюдаемые с самолёта проекции этих величин обозначены, как
. Наблюдаемые с самолёта проекции этих величин обозначены, как 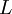 н и
н и 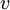 н. Очевидно, что
н. Очевидно, что
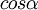 =
= 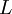 н /
н / 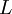 (8)
(8)
Чтобы определить 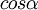 , воспользуемся тем, что ракета – это, в основном, цилиндрическое тело. Видимый же диаметр цилиндра
, воспользуемся тем, что ракета – это, в основном, цилиндрическое тело. Видимый же диаметр цилиндра 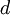 не зависит от его ориентации в пространстве. Разделив величины
не зависит от его ориентации в пространстве. Разделив величины 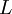 н и
н и 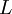 на не зависящую от угла
на не зависящую от угла  величину
величину 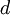 , получим из (8) простую формулу:
, получим из (8) простую формулу:
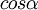 = (
= (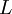 н
н (9)
(9)
Отношения  и
и 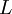 н
н легко измерить. Вид «лунной» ракеты общеизвестен (илл.13а). Её габариты соответствуют
легко измерить. Вид «лунной» ракеты общеизвестен (илл.13а). Её габариты соответствуют  . Отношение
. Отношение 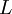 н
н  измерим по снимку илл.13б. Поскольку он недостаточно резок, то на результате измерения сказывается восприятие конкретного человека. Для исключения этого фактора
измерим по снимку илл.13б. Поскольку он недостаточно резок, то на результате измерения сказывается восприятие конкретного человека. Для исключения этого фактора 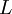 н и
н и 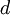 измерили независимо 6 человек (табл. илл.13б). При этом никакие «указания» в виде размеров, проставленных для читателя на илл.13, добровольным помощникам не давались. Усреднённое по шести людям значение
измерили независимо 6 человек (табл. илл.13б). При этом никакие «указания» в виде размеров, проставленных для читателя на илл.13, добровольным помощникам не давались. Усреднённое по шести людям значение 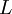 н
н  оказалось равным 7,9. Отсюда вычисляем по формуле (9)
оказалось равным 7,9. Отсюда вычисляем по формуле (9) 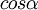 =
=  (
( = 440). Поэтому все размеры в направлении полёта ракеты кажутся нам меньше их реальных значений в
= 440). Поэтому все размеры в направлении полёта ракеты кажутся нам меньше их реальных значений в  раза, то есть в 1,4 раза. Мы можем очень просто преодолеть это искажение с помощью компьютера. Чтобы узнать, как выглядел бы конус Маха ракеты под прямым углом зрения, надо на снимке илл.3б растянуть масштаб вдоль вектора скорости в 1,4 раза. Результат этой операции и показан на илл.4.
раза, то есть в 1,4 раза. Мы можем очень просто преодолеть это искажение с помощью компьютера. Чтобы узнать, как выглядел бы конус Маха ракеты под прямым углом зрения, надо на снимке илл.3б растянуть масштаб вдоль вектора скорости в 1,4 раза. Результат этой операции и показан на илл.4.
Отметим, что для методов «по отставанию дымов» и «по боковым выбросам» нет необходимости учитывать фактор  . Дело в том, что изучаемые в них явления имеют общую цилиндрическую симметрию в противоположность только что рассмотренному случаю (конус Маха и цилиндр ракеты). Поэтому все визуальные искажения действуют на все явления и объекты, изучаемые по двум последним методам, одинаково.
. Дело в том, что изучаемые в них явления имеют общую цилиндрическую симметрию в противоположность только что рассмотренному случаю (конус Маха и цилиндр ракеты). Поэтому все визуальные искажения действуют на все явления и объекты, изучаемые по двум последним методам, одинаково.
Приложение 2.
О двух тезисах критики метода 1 (по конусу Маха) со стороны защитников NASA
Тезис №1. Кандидат геолого-минералогических наук, геофизик А.М. Тюрин пишет:[12] «Принципиальное замечание к статье А.И. Попова ([10] – А.П.) я уже привел: прямое применение формулы Маха для оценки скорости ракеты некорректно. Конфигурация фронта ударной волны от тел разной формы приведены в [Альбом]». Ну что ж, от критика, если он сведущ в поднятых им вопросах, логично ожидать, что он рассчитает число М корректно в противовес «некорректному» расчёту Попова. Увы, уважаемый геофизик ограничился тем, что провёл линии образующих конуса, нашёл угол ? равным 18о, и на этом его практический вклад в теорию вопроса закончился. А это настораживает. Советы давать любят очень многие, желающих же и умеющих делать гораздо меньше. Да, компетентен ли критик в затронутом им же вопросе?
А вот другой критик - Л. Георгиев из Технического Университета г. Варна, тоже сомневаясь в применимости простой формулы (2), не в пример А.М. Тюрину летом 2010 года сделал свой «точный расчёт». Этот расчёт, насыщенный многоэтажными формулами, графиками, и номограммами, Л. Георгиев прислал Попову А.И. и Покровскому С.Г. по е-мейл.[30]
Ну и что же дали эти «уточнения»? Как и следовало ожидать из простых физических соображений, гора точных расчётов «родила мышь». Автор данной статьи получил М = 3, Л. Георгиев - М = 2,86. На самом деле и это небольшое отличие (5%) связано с субъективными данными каждого автора, но никак не с математикой. Дело в том, что у любого автора одни только геометрические измерения угла конуса Маха (илл.4) и отношения 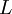 н
н  (илл.13б) дадут примерно такую же погрешность.
(илл.13б) дадут примерно такую же погрешность.
Например, по Попову угол ? на илл.4 равен 19,3о. Георгиев провёл линии вдоль конуса слегка иначе, и у него угол ? получился 20,8о. Для такого угла из простой формулы (2) получается значение М= 2,83, что только на 1% меньше, чем у Георгиева. Так что отличия в М возникли не из-за различий в математическом подходе, а из-за того, кто как проведёт ограничительные линии конуса. Размытые контуры конуса Маха оставляют известную свободу для личного восприятия. Поэтому правильнее брать некий средний угол по измерениям различных авторов, Давайте так и поступим. Тюрин определил ? как 18о, Попов – 19,3о, Георгиев – 20,3о. Среднее значение - 19,4о. Так чьё значение надёжнее, если у Попова измеренный угол ? отличается от среднего на 0,1о, а у Тюрина и Георгиева – на 1,4о?
А ведь есть ещё и второй субъективный фактор, который связан с определение отношения  н
н  . Здесь Попов для уменьшения влияния субъективного фактора воспользовался помощью шести помощников (илл.13б), а Л. Георгиев, похоже, положился только на своё личное зрительное восприятие. Но поскольку истинная скорость ракеты оказалась меньше официальной в 2 с лишним раза, то эти небольшие расхождения в подходе к геометрическим измерениям не столь уж и существенны. В физике увлечение такими совершенно несущественными мелочами иногда называют «ловлей блох». Именно этим занимается А.М. Тюрин и тем самым заставляет это делать и нас.
. Здесь Попов для уменьшения влияния субъективного фактора воспользовался помощью шести помощников (илл.13б), а Л. Георгиев, похоже, положился только на своё личное зрительное восприятие. Но поскольку истинная скорость ракеты оказалась меньше официальной в 2 с лишним раза, то эти небольшие расхождения в подходе к геометрическим измерениям не столь уж и существенны. В физике увлечение такими совершенно несущественными мелочами иногда называют «ловлей блох». Именно этим занимается А.М. Тюрин и тем самым заставляет это делать и нас.
Сказанное означает, что при одинаковом определении угла ? простая формула (2) даёт тот же результат по М, что и пространный расчёт Л. Георгиева. Что касается работы Л. Георгиева, то она всё же принесла определённую пользу в том плане, что, её автор, сам не желая того, доказал ненужность его громоздкого «точного» подхода к решению очень простой задачи определения скорости ракеты. Критику же А.М. Тюрина, не содержащую собственного расчёта М, и неверную по существу, можно считать совершенно бесполезной.
Тезис №2. Получив практически полное совпадение с Поповым по числу М, Л. Георгиев решил помочь NASA иным способом. Он пишет:[31] «M=2,9, но температура и состав газов сильно влияют. Газы (имеются в виду горячие газы от «взрыва» - А.П.) не только достигли, но и обошли фронт. Теперь они возвращаются назад, но в скачке всё ещё стоит значительная их часть. В июне этого года я смоделировал ракету "Сатурн-5" в этот момент программой "Fluent" и получил число Маха 2,9. Но температура смеси газов гораздо большая, чем температура набегающего воздуха (вероятно тысячи градусов!), а, следовательно, и скорость звука, прямо пропорциональная квадратному корню температуры, а отсюда и скорость самой ракеты, тоже значительно выше. Следовательно, без определения температуры и состава газов такой метод расчета скорости ракеты ничего не дает. Лучше использовать точные значения NASA».
Итак, поскольку у Георгиева значение М=2,9, то есть практически то же самое, что и у Попова, то надо максимально завысить скорость звука  . (Напомним:
. (Напомним:  ). И пошёл в ход аргумент о «тысячах градусов» с конечным призывом положиться на честность NASA. Но и этот тезис не выдерживает простого взгляда на картину конуса у острия ракеты. Посмотрим её ещё раз и выделим на ней три области: 1, 2 и 3.
). И пошёл в ход аргумент о «тысячах градусов» с конечным призывом положиться на честность NASA. Но и этот тезис не выдерживает простого взгляда на картину конуса у острия ракеты. Посмотрим её ещё раз и выделим на ней три области: 1, 2 и 3.
Область 1. Здесь относительно слабые остаточные продукты от «взрыва» за границу скачка плотности воздуха не прорвались. Снаружи границы конуса – холодный окружающий воздух, а именно в нём и распространяется ударная волна конуса Маха. Естественно со скоростью звука соответствующей температуре этой холодной среды (~350 м/с). О каких тысячах градусов рассуждает Георгиев, глядя на участок 1, трудно понять. Область 1 – это область классического неискажённого конуса Маха. Именно её мы и использовали для расчёта.
Область 2 не использовалась нами для расчёта, но знакомство с ней позволит дополнительно убедиться в правильности понимания общей физической картины. Здесь от тела ракеты в поперечном направлении бьют яркие, плотные и явно горячие продукты «взрыва». Ничего похожего в области 1 не видно. Тем не менее, фронт уплотнения воздуха, но они не «обошли» его, как о том пишет Георгиев. Набегающий поток зажал их в тиски скачка уплотнения. При этом граница уплотненного воздуха чуть отодвинулась, но не изменила своего направления. Следовательно, скорости и направления распространения ударной волны на участках 1 и 2 одинаковы. Но ведь газы и дымы в области 2, очевидно, горячее, чем в области 1. Следовательно, температура газов внутри конуса существенного влияния на границы конуса не оказывает. И это естественно. Потому что, как сказано, ударный фронт конуса Маха движется наружу и через окружающий холодный воздух. Поэтому скорость его равна скорости звука именно в этом холодном воздухе (~350 м/с). Пока что всё происходит не так, как о том пишет Георгиев.
Область 3. Здесь, действительно, фронт конуса прорван, да и сам конус просто уничтожен. Но нам от этого «ни холодно, ни жарко». Потому что конус Маха не изучают там, где его нет. Мы проделали свои измерения в области 1 по чистому, неискажённому конусу Маха. Так что рассуждения Л. Георгиева о прорывах фронта, о тысячах градусов температуры к нашим измерениям и расчётам отношения не имеют.
Автор благодарит специалиста по газодинамике, профессора МИФИ, физика-теоретика, доктора физико – математических наук Боговалова А.В., взявшего на себя труд рецензирования первого раздела главы, включая приложения. Также автор благодарит Соловьяна А.Г. за помощь в оформлении иллюстративных материалов.
Примечания
- ↑ , Черток Б.Е. Ракеты и люди. Книга 4. Лунная гонка – М.: Машиностроение, 1999.-576с Глава 9.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 клип
- ↑ 3,0 3,1 APOLLO/SATURN V POSTFLIGHT TRAJECTORY - AS-506 команда на отделение первой ступени согласно NASA проходит на высоте 66км (по Table 3-III) и 66,7км (по Table 3-IV) в момент времени (162,3с по Table 3-I и по Table 3-IV), скорость в момент разделения 2,77 км/с, что за вычетом скорости вращения Земли составляет примерно 2,4км/с относительно окружающего воздуха. Ошибка цитирования Неверный тег
<ref>: название «D» определено несколько раз для различного содержимого - ↑ [1]
- ↑ [2]
- ↑ 6,0 6,1 6,2 6,3 С.Г. Покровский. Попасть на Луну американцы не могли // Актуальные проблемы современной науки. 2007. № , с.152-166.
- ↑ 7,0 7,1 7,2 7,3 Попасть на Луну американцы не могли
- ↑ 8,0 8,1 8,2 8,3 «Уточнённая оценка скорости «Сатурна-5»
- ↑ 9,0 9,1 9,2 9,3 [3] Ошибка цитирования Неверный тег
<ref>: название «J» определено несколько раз для различного содержимого Ошибка цитирования Неверный тег<ref>: название «J» определено несколько раз для различного содержимого Ошибка цитирования Неверный тег<ref>: название «J» определено несколько раз для различного содержимого - ↑ 10,0 10,1 10,2 [4]
- ↑ [5]
- ↑ 12,0 12,1 А.М. Тюрин. «К вопросу об оценке скорости ракеты «Сатурн-5»»
- ↑ 13,0 13,1 6Мб - снимок илл.2
- ↑ 14,0 14,1 41Кб - снимок илл.2
- ↑ 15,0 15,1 - краткое описание условий съёмки снимка илл.2. Высота полёта самолёта, расстояние до ракеты и др.
- ↑ 16,0 16,1 (A-LOTS - Airborne Lightweight Optical Tracking System) Общее описание самолётной оптической системы наблюдения
- ↑ 17,0 17,1 (ARIA 61-0327 June 1967 - Bob Burns Randy Losey). Самолёт-носитель системы.
- ↑ 18,0 18,1 (A-LOTS Pod - John GourleyRandy Losey)
- ↑ 19,0 19,1 (PanAm Clipper Randy Losey). Место установки системы.
- ↑ 20,0 20,1 См. также: Airborne Telescope Observations
- ↑ [6]
- ↑ [7]
- ↑ [8]
- ↑ 24,0 24,1 [9]
- ↑ [10]
- ↑ А Кудрявец
- ↑ [11]
- ↑ [12]
- ↑ [13]
- ↑ Latchezar I. Georgiev. A goniometric rocket velocity computation algorithm
- ↑ [14]