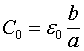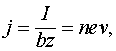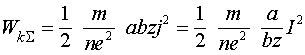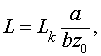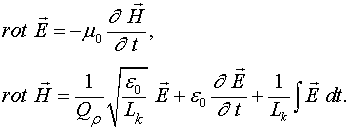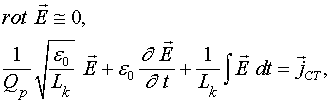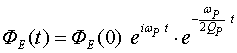Поперечный плазменный резонанс и электромагнитное излучение ядерного взрыва
| Ф.Ф. Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Введение
При ядерных взрывах возникает электромагнитное излучение в очень широком диапазоне частот от жесткого рентгеновского излучения до радиочастотного. Если излучение в рентгеновском и световом диапазоне можно объяснить излучением отдельных атомов и молекул в раскалённой плазме ядерного взрыва, то удовлетворительного объяснения природы излучения в радиодиапазоне пока нет. Такое излучение может быть следствием каких-то коллективных процессов, приводящих к образованию колеблющихся электрических диполей. Известно, что в плазме могут иметь место плазменные ленгмюровские колебания, однако эти колебания являются продольными и излучать электромагнитные волны не могут. Ниже будет показано, что в ограниченной незамагниченной плазме может иметь место и поперечный плазменный резонанс, результатом которого и может быть радиочастотное излучение http://arxiv.org/abs/physics/0506081 .
Поперечный плазменный резонанс в незамагниченной плазме
Теперь покажем, как плохое понимание физики процессов, имеющих место в проводящих средах, привело к тому, что оказалось незамеченным интересное физическое явление, которое может быть названо поперечный плазменный резонанс в незамагниченной плазме. Это, ранее неизвестное явление, может иметь важные технические приложения http://fmnauka.narod.ru/asd.pdf.
Известно, что ленгмюровский резонанс является продольным. Но продольный резонанс не может излучать поперечные радиоволны. Однако при взрывах ядерных зарядов, в результате которых образуется очень горячая плазма, имеет место электромагнитное излучение в очень широком диапазоне частот, вплоть до длинноволнового радиодиапазона. На сегодняшний день нет тех физических механизмов, которые смогли бы объяснить возникновение такого излучения. О существовании в незамагниченной плазме каких-либо других резонансов, кроме ленгмюровского, ранее известно не было, но в ограниченной плазме может существовать и поперечный резонанс, и частота такого резонанса совпадает с частотой ленгмюровского резонанса, т.е. эти разонансы являются вырожденными. Именно этот резонанс может быть причиной излучения радиоволн при взрывах ядерных зарядов.
Для выяснения условий возбуждения такого резонанса рассмотрим длинную линию, состоящую из двух идеально проводящих плоскостей, как показано на рис.1
Рис. 1 Двухпроводная линия, состоящая из двух идеально проводящих плоскостей
Погонная (приходящаяся на единицу длины) емкость и индуктивность такой линии без учёта краевых эффектов определяются соотношениями:
Поэтому с ростом длины линии ее суммарная емкость
 и суммарная индуктивность
и суммарная индуктивность  увеличиваются пропорционально ее длине.
увеличиваются пропорционально ее длине.
Если в разомкнутую линию поместить плазму, носители заряда в которой могут двигаться без трения, и в поперечном направлении пропустить через плазму ток ![]() , то заряды в связи с наличием у них массы, двигаясь с определенной скоростью, будут накапливать кинетическую энергию. Заметим, что здесь не рассматриваются технические вопросы, как и каким образом можно разместить плазму между плоскостями линии. В данном случае рассматриваются только принципиальные вопросы, касающиеся ранее неизвестного поперечного плазменного резонанса в незамагниченной плазме.
Поскольку поперечная плотность тока в такой линии определяется соотношением
, то заряды в связи с наличием у них массы, двигаясь с определенной скоростью, будут накапливать кинетическую энергию. Заметим, что здесь не рассматриваются технические вопросы, как и каким образом можно разместить плазму между плоскостями линии. В данном случае рассматриваются только принципиальные вопросы, касающиеся ранее неизвестного поперечного плазменного резонанса в незамагниченной плазме.
Поскольку поперечная плотность тока в такой линии определяется соотношением
то суммарная кинетическая энергия всех движущихся зарядов будет записана:
(1.1)
Соотношение (1.1) связывает кинетическую энергию, накопленную в линии, с квадратом тока, поэтому коэффициент, стоящий в правой части этого соотношения перед квадратом тока, является суммарной кинетической индуктивностью линии.
(1.2)
Таким образом, величина
(1.3)
представляет удельную кинетическую индуктивность. Соотношение (1.3) получено для случая постоянного тока, когда токовое распределение является однородным.
В дальнейшем для большей наглядности полученных результатов, наряду с математическим их представлением, будем пользоваться методом эквивалентных схем. Отрезок, рассмотренной линии, длинной ![]() может быть представлен в виде эквивалентной схемы, показанной на рис. 2 (а).
может быть представлен в виде эквивалентной схемы, показанной на рис. 2 (а).
Из соотношения (2) видно, что в отличие от ![]() и
и ![]() величина
величина ![]() с ростом
с ростом ![]() не увеличивается, а уменьшается. Связано это с тем, что с ростом
не увеличивается, а уменьшается. Связано это с тем, что с ростом ![]() количество параллельно включенных индуктивных элементов растет.
количество параллельно включенных индуктивных элементов растет.
Эквивалентная схема участка линии, заполненной бездиссипативной плазмой, показана на рис. 2 (б). Сама линия при этом будет эквивалентна параллельному контуру с сосредоточенными параметрами:
последовательно с которым включена индуктивность
Но если вычислить резонансную частоту такого контура, то окажется, что эта частота вообще ни от каких размеров не зависит, действительно:
Получен очень интересный результат, который говорит о том, что резонансная частота рассмотренного макроскопического резонатора не зависит от его размеров. Может создаться впечатление, что это ленгмюровский резонанс, т.к. полученное значение резонансной частоты в точности соответствует значению частоты ленгмюровского резонанса. Но известно, что такой резонанс характеризует продольные волны, в то время как в длинной линии имеют место только поперечные волны. В этом случае величина фазовой скорости в направлении равна бесконечности и волновой вектор ![]() .
.
Рис. 2.
- а – эквивалентная схема отрезка двухпроводной линии;
- б – эквивалентная схема отрезка двухпроводной линии, заполненной бесдиссипативной плазмой;
- в - эквивалентная схема отрезка двухпроводной линии, заполненной диссипативной плазмой.
При этом волновое число определяется соотношением:
(1.4)
а групповая и фазовая скорости
(1.5)
(1.6)
где  - скорость света в вакууме.
- скорость света в вакууме.
Для данного случая фазовая скорость электромагнитной волны равна бесконечности, что соответствует поперечному резонансу на плазменной частоте. Следовательно, в каждый момент времени распределение полей и токов в такой линии однородно и не зависит от координаты ![]() , а ток в плоскостях линии в направлении
, а ток в плоскостях линии в направлении ![]() отсутствует. Это, с одной стороны, означает, что индуктивность
отсутствует. Это, с одной стороны, означает, что индуктивность ![]() не будет оказывать влияния на электродинамические процессы в такой линии, а вместо проводящих плоскостей могут быть использованы любые плоскости или устройства, ограничивающие плазму. Ещё раз отметим, что в данном случае обсуждается только принципиальная сторона вопроса, т.к., например, газоразрядную плазму ограничить для данных целей плоскостями нельзя, т.к. на эти плоскости будут оседать заряды. Возможно, это должна быть плазма в твердом теле, или газоразрядная плазма в магнитной ловушке или плазма ядерного взрыва, ограниченная границами облака взрыва.
не будет оказывать влияния на электродинамические процессы в такой линии, а вместо проводящих плоскостей могут быть использованы любые плоскости или устройства, ограничивающие плазму. Ещё раз отметим, что в данном случае обсуждается только принципиальная сторона вопроса, т.к., например, газоразрядную плазму ограничить для данных целей плоскостями нельзя, т.к. на эти плоскости будут оседать заряды. Возможно, это должна быть плазма в твердом теле, или газоразрядная плазма в магнитной ловушке или плазма ядерного взрыва, ограниченная границами облака взрыва.
Из соотношений (1.4) , (1.5) и (1.6) нетрудно видеть, что в точке ![]() имеет место поперечный резонанс с бесконечной добротностью. При наличии потерь в резонаторе будет иметь место затухание, а в длинной линии в этом случае
имеет место поперечный резонанс с бесконечной добротностью. При наличии потерь в резонаторе будет иметь место затухание, а в длинной линии в этом случае ![]() , и в линии будет распространяться затухающая поперечная волна, направление распространения которой будет нормально направлению движения зарядов. Следует отметить, что факт существования такого резонанса ранее осознан не был и другими авторами не описан.
, и в линии будет распространяться затухающая поперечная волна, направление распространения которой будет нормально направлению движения зарядов. Следует отметить, что факт существования такого резонанса ранее осознан не был и другими авторами не описан.
Перед тем, как перейти к более подробному рассмотрению данного вопроса, остановимся на энергетических процессах, имеющих место в рассмотренной линии в случае отсутствия потерь.
Характеристическое сопротивление плазмы, дающее отношение поперечных компонент электрического и магнитного полей, определяется соотношением
где  - характеристическое (волновое) сопротивление вакуума.
- характеристическое (волновое) сопротивление вакуума.
Полученное значение ![]() характерно для поперечных электрических волн в волноводах. Видно, что когда
характерно для поперечных электрических волн в волноводах. Видно, что когда ![]() , то
, то ![]() , а
, а ![]() . В том случае, когда
. В том случае, когда ![]() >
> ![]() в плазме существует и электрическая и магнитная составляющая поля. Удельная энергия этих полей запишется:
в плазме существует и электрическая и магнитная составляющая поля. Удельная энергия этих полей запишется:
Таким образом, энергия, заключенная в магнитном поле, в  раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что данное рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волн электрического и магнитного полей, несущих электрическую и магнитную энергии, в плазме существует еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается:
раз меньше, чем энергия, заключенная в электрическом поле. Отметим, что данное рассмотрение, которое является традиционным в электродинамике, является не полным, т.к. при этом не учтен еще один вид энергии, а именно кинетическая энергия носителей заряда. Оказывается, что кроме волн электрического и магнитного полей, несущих электрическую и магнитную энергии, в плазме существует еще и третья - кинетическая волна, несущая кинетическую энергию носителей тока. Удельная энергия этой волны записывается:
Таким образом, полная удельная энергия записывается как
Следовательно, для нахождения полной энергии, аккумулированной в единице объема плазмы, учет только полей ![]() и
и ![]() недостаточен. В точке
недостаточен. В точке ![]() выполняются соотношения:
выполняются соотношения:
т.е. магнитное поле в плазме отсутствует, и плазма представляет макроскопический электромеханический резонатор с бесконечной добротностью, резонирующий на частоте ![]() .
.
Поскольку при частотах ![]() >
>![]() волна, распространяющаяся в плазме, несет на себе три вида энергии: магнитную, электрическую и кинетическую, то такую волну можно назвать электромагнитокинетической. Кинетическая волна представляет из себя волну плотности тока
волна, распространяющаяся в плазме, несет на себе три вида энергии: магнитную, электрическую и кинетическую, то такую волну можно назвать электромагнитокинетической. Кинетическая волна представляет из себя волну плотности тока  . Эта волна сдвинута по отношению к электрической волне на угол
. Эта волна сдвинута по отношению к электрической волне на угол ![]() .
.
До сих пор рассматривался физически нереализуемый случай, когда потери в плазме отсутствуют, что соответствует бесконечной добротности плазменного резонатора. Если потери имеются, причем совершенно не важно какими физическими процессами такие потери обусловлены, то добротность плазменного резонатора будет конечной величиной. Для такого случая уравнения Максвелла будут иметь вид:
(1.7)
Наличие потерь учитывается членом ![]() , причем, употребляя возле проводимости индекса
, причем, употребляя возле проводимости индекса ![]() , тем самым подчеркивается, что нас не интересует сам механизм потерь, а интересует только сам факт их существования. Величину
, тем самым подчеркивается, что нас не интересует сам механизм потерь, а интересует только сам факт их существования. Величину ![]() определяет добротность плазменного резонатора. Для измерения
определяет добротность плазменного резонатора. Для измерения ![]() следует выбрать отрезок линии длиной
следует выбрать отрезок линии длиной ![]() , величина которого значительно меньше длины волны в диссипативной плазме. Такой отрезок будет эквивалентен контуру с сосредоточенными параметрами:
, величина которого значительно меньше длины волны в диссипативной плазме. Такой отрезок будет эквивалентен контуру с сосредоточенными параметрами:
(1.8)
(1.9)
(1.10)
где ![]() – проводимость, подключенная параллельно
– проводимость, подключенная параллельно ![]() и
и ![]() .
.
Проводимость и добротность в таком контуре связаны соотношением:
откуда, учитывая (1.8 – 1.10), получаем:
(1.11)
Таким образом, измеряя собственную добротность плазменного резонатора, можно определить ![]() . Используя (1.2) и (1.11) получим:
. Используя (1.2) и (1.11) получим:
(1.12)
Эквивалентная схема такой линии, заполненной диссипативной плазмой, представлена на рис. 2 (в).
Рассмотрим решение системы уравнений (1.12) в точке ![]() , при этом, поскольку
, при этом, поскольку
Получаем
Эти соотношения и определяют волновые процессы в точке резонанса.
Если потери в плазме, заполняющей линию малы, а к линии подключен сторонний источник тока, то можно положить:
(1.13)
где ![]() – плотность сторонних токов.
– плотность сторонних токов.
Проинтегрировав (1.13) по времени и разделив обе части на ![]() , получим
, получим
(1.14)
Если (1.14) проинтегрировать по поверхности нормальной к вектору ![]() и ввести электрический поток как
и ввести электрический поток как ![]() получим:
получим:
(1.15)
Уравнение (1.15) является уравнением гармонического осциллятора с правой частью, характерное для двухуровневых лазеров [1]. Если источник возбуждения отключить, то соотношение (1.14) представляет “холодный” лазерный резонатор, в котором колебания будут затухать по экспоненциальному закону
т.е. макроскопический электрический поток ![]() будет осцилировать с частотой
будет осцилировать с частотой ![]() , время релаксации при этом определяется соотношением:
, время релаксации при этом определяется соотношением:
Задача создания лазера заключается теперь лишь в умении возбудить такой резонатор.
Если резонатор возбуждается сторонними токами, то такой резонатор для этих токов представляет полосовой фильтр с резонансной частотой равной плазменной частоте с полосой пропускания  .
.
Другим важным практическим применением поперечного плазменного резонанса является возможность его использование для разогрева и диагностики плазмы. Если добротность плазменного резонатора велика, что может быть получены высокие уровни электрических полей, а значит и высокие энергии носителей зарядов.
Таким образом, мы установили, что в незамагниченной ограниченной плазме может иметь место поперечный плазменный резонанс, который и может служить источником излучения, частота которого зависит от плотности плазмы. В процессе эволюции облака взрыва ядерного заряда плотность плазмы колеблется в самых широких пределах, следовательно, и излучаемые такой плазмой частоты могут варьироваться в самых широких пределах.
Однако возникает ещё один важный вопрос. Для возникновения колебаний в ограниченной плазме недостаточно наличия самой плазмы, нужны ещё и механизмы, которые приводят к начальному пространственному коллективному разделению (неустойчивости) больших групп зарядов, которые в последующем и будут осуществлять затухающий колебательный процесс дипольного характера, приводящих к излучению.
Механизм плазменных неустойчивостей в облаке взрыва ядерного заряда
Топология электрического импульса термоядерного взрыва, произведённого в космосе, показана на рис. 2.
Рис. 2. Экспериментальная зависимость амплитуды электрического импульса ядерного взрыва от времени.
Особенностью импульса является его очень маленькая длительность, которая составляет порядка 100 нс. Это означает, что за такое короткое время происходит и детонация ядерного топлива и его охлаждение до температур значительно ниже тех, которые имеют место в момент детонации. Поскольку основное тепловое излучение идёт с поверхности облака, то очевидным является большой градиент температур в самом облаке. С точки зрения представлений современной электродинамики и теории относительности, такие градиенты тоже не могут дать зарядового разделения, поскольку в СТО заряд является инвариантом скорости.
Однако концепция скалярно-векторного потенциала, представленная в работах http://fmnauka.narod.ru/asd.pdf http://arxiv.org/abs/physics/0402084 , указывает на то, что заряд не является инвариантом скорости, а зависит от его относительной скорости. Коротко напомним эту концепцию.
Законы магнитоэлектрической и электромагнитной индукции имеют симметричную форму и записываются следующим образом:
(2.1)
или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея. Штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе http://fmnauka.narod.ru/asd.pdf . Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе http://fmnauka.narod.ru/asd.pdf . Электрическое поле 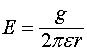 за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом :
(2.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда.
Но такая зависимость скалярного потенциала от скорости означает и зависимость от неё самого заряда. Именно это обстоятельство и приводит к зарядовому разбалансу в плазме, в которой имеются большие градиенты температур. Именно этот зарядовый разбаланс и его эволюция в процессе дальнейшей быстрой эволюции температурных градиентов в плазме и приводит к неустойчивостям, возбуждающим поперечные плазменные колебания в облаке ядерного взрыва.
Следует сказать, что подобный процесс имеет место и на поверхности Солнца, где имеются мощные магнитные поля. Эти поля являются результатом того, что отдельные участки солнечной поверхности имеют разную температуру и в связи с зарядовым разбалансом, который мы объяснили выше, между такими участками текут большие токи, которые и создают указанные поля.
Литература
- 1. Ярив А. Квантовая электродинамика и нелинейная оптика. М: Сов. радио, 1973.- 454 с.