Обсуждение:В чём просчитались теоретики, введя обобщённый импульс движущегося заряда
Работа неверна. При переходе от известной функции Лагранжа для взаимодействия заряженной частицы с электромагнитным полем,
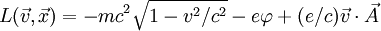 - см формулу (23.10) из критикуемой работы, и обозначения там же - в данном случае, когда Лагранжиан вообще не может быть разделен на кинетическую и потенциальную энергию, грубо ошибочно полагать, что
- см формулу (23.10) из критикуемой работы, и обозначения там же - в данном случае, когда Лагранжиан вообще не может быть разделен на кинетическую и потенциальную энергию, грубо ошибочно полагать, что 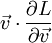 "по определению, есть удвоенная кинетическая энергия". Следует сначала ввести полную энергию, то есть функцию Гамильтона, чтобы разговор об энергии был бы хоть сколь-нибудь предметным. По определению, вводя функцию Гамильтона по известной общей формуле (следую формуле (16,6) из Л.Д.Дандау и Е.М.Лифшиц, Теория поля, М.: Наука, 1972.), получаем:
"по определению, есть удвоенная кинетическая энергия". Следует сначала ввести полную энергию, то есть функцию Гамильтона, чтобы разговор об энергии был бы хоть сколь-нибудь предметным. По определению, вводя функцию Гамильтона по известной общей формуле (следую формуле (16,6) из Л.Д.Дандау и Е.М.Лифшиц, Теория поля, М.: Наука, 1972.), получаем:
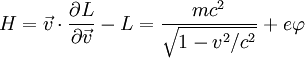
(3)
Второй член в этой формуле согласно Л.Д.Дандау и Е.М.Лифшиц, Теория поля, М.: Наука, 1972 (см (19,2)) может быть назван потенциальной энергией, а первый, с некоторыми оговорками - кинетической. Таким образом смехотворное "опровержение" известного выражения для обобщенного импульса в [1] вызвана полным непониманием, что это вообще такое - обобщенный импульс и энергия.
Еще более смехотворно рассуждение о включение в потенциальную энергию члена
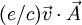 , который, как мы видим из (3), вообще не входит в энергию. Последний общеизвестный факт тесно связан с другим общеизвестным фактом, что (равное ротору от вектор-потенциала) магнитное поле не совершает работу над движущимся зарядом. Тем самым, разумеется, опровергается и соответствующее место в монографии Ф.Ф.Менде. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике. Харьков: НТМТ, 2010 - которая, впрочем, обессмысливается значительно раньше, чем в ней вводится "потенциальная энергия вектор-потенциала".
, который, как мы видим из (3), вообще не входит в энергию. Последний общеизвестный факт тесно связан с другим общеизвестным фактом, что (равное ротору от вектор-потенциала) магнитное поле не совершает работу над движущимся зарядом. Тем самым, разумеется, опровергается и соответствующее место в монографии Ф.Ф.Менде. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике. Харьков: НТМТ, 2010 - которая, впрочем, обессмысливается значительно раньше, чем в ней вводится "потенциальная энергия вектор-потенциала".