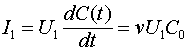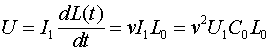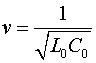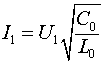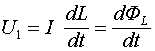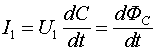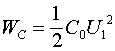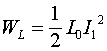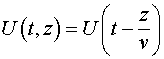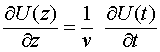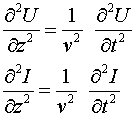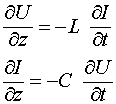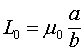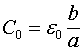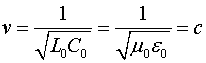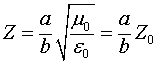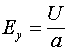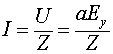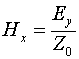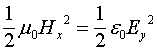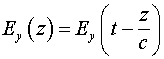Новый способ получения волнового уравнения
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
До сих пор в электродинамике и радиотехнике было известно только два способа вывода волнового уравнения. Первый основан на использовании уравнений Максвелла, второй - телеграфных уравнений. Как в том, так и в другом случае для записи волновых уравнений необходимо знание вторых производных по времени и координате электрических и магнитных полей, если речь идёт о свободном пространстве, или таких же производных напряжений и токов, если речь идёт о длинных линиях. Но как быть, если, например, эти производные равны нулю? Ответа на этот вопрос ранее не было.
Процессы, рассмотренные в § 10-12 работы http://fmnauka.narod.ru/Pro1.pdf, касаются цепей с сосредоточенными параметрами, когда распределение разностей потенциалов и токов в рассмотренных элементах можно считать однородным. Однако имеются цепи, например длинные линии, в которых разности потенциалов и токи не являются пространственно однородными. Эти процессы описываются волновыми уравнениями, которые могут быть получены из уравнений Максвелла или при помощи телеграфных уравнений, но физика самого явления нам не ясна.
Воспользуемся результатами, полученными в указанных параграфах для рассмотрения процессов, происходящих в длинных линиях, в которых емкость и индуктивность являются распределенными параметрами. Предположим, что погонная (приходящаяся на единицу длины) емкость и индуктивность такой линии составляют соответственно ![]() и
и ![]() . Если к такой линии подключить источник постоянного напряжения
. Если к такой линии подключить источник постоянного напряжения ![]() , то фронт этого напряжения будет распространяться в линии с какой-то скоростью
, то фронт этого напряжения будет распространяться в линии с какой-то скоростью ![]() , и текущая координата этого фронта определится соотношением
, и текущая координата этого фронта определится соотношением ![]() . При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
. При этом суммарная величина заряженной ёмкости и величина суммарной индуктивности, по которой протекает ток, отсчитываемые от начала линии до места нахождения фронта напряжения, будут изменяться по закону:
Источник напряжения ![]() будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением должен течь ток:
будет при этом заряжать увеличивающуюся емкость линии, для чего от источника к заряжаемой линии в соответствии с соотношением должен течь ток:
(1) Этот ток будет протекать через проводники линии, обладающие индуктивностью. Но, поскольку индуктивность линии в связи с движением фронта напряжения, тоже увеличивается, на ней будет наблюдаться падение напряжения:
Но падение напряжения на проводниках линии по абсолютной величине равно напряжению, приложенному к её входу, поэтому в последнем выражении следует допустить, что ![]() . С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения
. С учетом этого сразу находим, что скорость движения фронта напряжения при заданных погонных параметрах и при наличии на входе линии постоянного напряжения ![]() должна составлять
должна составлять
(2)
Это выражение соответствует скорости распространения электромагнитных колебаний в самой линии. Следовательно, если к бесконечно длинной линии подключить источник напряжения, то в ней будет иметь место саморасширение и ёмкостного и индуктивного потоков, заполняющих линию энергией, и скорость фронта постоянного напряжения и тока будет равна скорости распространения электромагнитных колебаний в такой линии. Такую волну будем называть электротоковой. Интересно отметить, что полученный результат не зависит от вида функции ![]() , т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (2). Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью
, т.е. к линии может быть подключен как источник постоянного напряжения, так и источник, напряжение которого меняется по любому закону. Во всех этих случаях величина локального значения напряжения на входе линии будет распространяться вдоль неё со скоростью описываемой соотношением (2). Этот результат мог быть до сих пор получен только путём решения волнового уравнения, но в данном случае он указывает на физическую причину такого распространения, и даёт физическую картину самого процесса. Он показывает, что сам процесс распространения связан с энергетическими процессами заполнения линии ёмкостной и индуктивной энергией. Этот процесс происходит таким образом, что фронт волны, распространяясь со скоростью ![]() , оставляет за собой линию, заряженную до разности потенциалов
, оставляет за собой линию, заряженную до разности потенциалов ![]() , что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток
, что соответствует заполнению линии электростатической энергией электрического поля. На участке же линии от источника напряжения и до фронта волны течет ток ![]() , что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
, что соответствует заполнению линии на этом участке энергией, которая связана с движением зарядов по проводникам линии, обладающих индуктивностью.
Величину тока в линии можно получить, подставив значения скорости распространения фронта волны, определяемого соотношением (2), в соотношение (1).
Сделав эту подстановку, получим
где 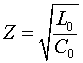 - волновое сопротивление линии.
- волновое сопротивление линии.
В данном случае
Так точно
Видно, что правила потока и для индуктивной и для ёмкостной самоиндукции соблюдаются и в этом случае.
Таким образом, процессы распространения разности потенциалов вдоль проводников длинной линии и постоянного тока в ней являются связанными и взаимно дополняющими друг друга, и существовать друг без друга не могут. Такой процесс можно называть ёмкостно-индуктивной самопроизвольной параметрической самоиндукцией. Такое название связано с тем, что расширение потоков происходят самопроизвольно и характеризуют скорость процесса заполнения линии энергией. Из выше изложенного становится понятной связь между энергетическими процессами и скоростью распространения фронтов волны в длинных линиях. Поскольку при излучении электромагнитных волн свободное пространство тоже является передающей линией, то подобные законы должны характеризовать и распространение в таком пространстве.
Что будет, например, в том случае, если в качестве одного из проводников длинной линии взять спираль, или как это принято называть, длинный соленоид. Очевидно, в этом случае скорость распространения фронта напряжения в такой линии уменьшится, поскольку погонная индуктивность линии увеличится. При этом такому распространению будет сопутствовать процесс распространения не только внешних, по отношению к соленоиду полей и токов, но и процесс распространения магнитного потока внутри самого соленоида и скорость распространения такого потока будет равна скорости распространения электромагнитной волны в самой линии.
Зная ток и напряжение в линии, можно вычислить удельную энергию, заключенную в погонной ёмкости и индуктивности линии. Эти энергии будут определяться соотношениями:
(3)
(4)
Теперь обсудим вопрос о длительности фронта электротоковой волны и о том, какое пространство этот фронт будет занимать в самой линии. Ответ на первый вопрос определяется свойствами самого источника напряжения, т.к. локальная производная ![]() на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время
на входе линии зависит от переходных процессов в самом источнике и в том устройстве, при помощи которого такой источник подключается к линии. Если процесс установления напряжения на входе линии будет длиться какое-то время ![]() , то в линии он займет участок длиной
, то в линии он займет участок длиной ![]() . Если к линии приложить напряжение, меняющееся со временем по закону
. Если к линии приложить напряжение, меняющееся со временем по закону ![]() , то это же значение функции будет наблюдаться в любой точке линии на расстоянии
, то это же значение функции будет наблюдаться в любой точке линии на расстоянии ![]() от ее начала с запаздыванием
от ее начала с запаздыванием ![]() .
.
Таким образом, функция
(5)
может быть названа функцией распространения, т.к. она устанавливает связь между локальными временными и пространственными значениями функции в линии. Длинная линия является устройством, которое локальные производные напряжения по времени на входе линии превращает в пространственные производные в самой линии. На основании функции распространения (5) можно установить связь между локальными и пространственными производными в длинной линии. Очевидно, что
Важно отметить, что сам процесс распространения в данном случае обязан естественному саморасширению электрического поля и тока в линии, и он подчиняется правилам параметрической самоиндукции. Во-вторых, для решения волновых уравнений длинных линий
(6)
полученных из телеграфных уравнений
требуется знание вторых производных напряжений и токов.
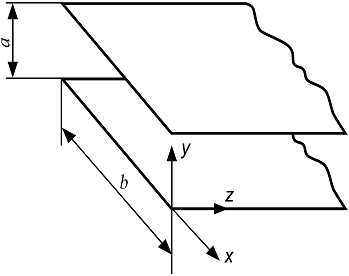
Но как быть, если на вход линии подаётся напряжение, у которого вторая производная равна нулю (случай, когда напряжение источника меняется по линейному закону)? Ответа на этот вопрос уравнения (6) не дают. Используемый метод даёт простой ответ на такой вопрос. При рассмотрении процессов в длинной линии фигурировали такие понятия как погонная емкость и индуктивность, а также токи и напряжения в линии. Однако в электродинамике, основанной на уравнениях Максвелла, нет таких понятий как емкость и индуктивность, а есть понятия электрической и магнитной проницаемости среды. В проведенном рассмотрении также отсутствовали такие понятия как электрические и магнитные поля. Покажем, как перейти от таких категорий как «погонная индуктивность и ёмкость», и «ток» и «напряжение» в линии к таким понятиям как «диэлектрическая и магнитная проницаемость», а также «электрическое и магнитное поле». Для этого возьмем простейшую конструкцию линии, расположенную в вакууме, как показано на рис. 1.
Рис. 1 Двухпроводная линия, состоящая из двух идеально проводящих плоскостей
Будем считать, что ![]() >>
>>![]() и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
и краевые эффекты можно не учитывать. Тогда между погонными параметрами линии и магнитной и диэлектрической проницаемостями будет существовать следующая связь:
(7)
(8)
где ![]() и
и ![]() - магнитная и диэлектрическая проницаемость вакуума.
Фазовая скорость в такой линии будет определяться соотношением:
- магнитная и диэлектрическая проницаемость вакуума.
Фазовая скорость в такой линии будет определяться соотношением:
где ![]() - скорость распространения света в вакууме.
- скорость распространения света в вакууме.
Волновое сопротивление рассмотренной линии будет равно:
где 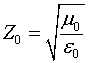 - волновое сопротивление свободного пространства.
- волновое сопротивление свободного пространства.
Кроме этого при соблюдении условия ![]() получаем равенство
получаем равенство ![]() . Это означает, что магнитная проницаемость
. Это означает, что магнитная проницаемость ![]() играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство
играет роль продольной удельной индуктивности вакуума. В этом случае соблюдается также равенство ![]() . Это означает, что диэлектрическая проницаемость
. Это означает, что диэлектрическая проницаемость ![]() играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и
играет роль поперечной удельной ёмкости вакуума. В такой интерпретации и ![]() , и
, и ![]() приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
приобретают ясный физический смысл и, так же как в длинной линии, обеспечивают процесс распространения электромагнитной волны в свободном пространстве.
Рассмотрение электромагнитной волны в длинной линии можно рассматривать как заполнение пространства, находящегося между её проводниками, особым видом материи, которую представляют электрические и магнитные поля. Математически можно считать, что эти поля сами обладают удельной энергией и при их помощи можно передавать энергию по линиям передач. Если же рассматривать процессы, протекающие при излучении электромагнитных волн при помощи какой-либо антенны, то его можно рассматривать также как заполнение свободного пространства этим видом материи. Однако геометрический вид полей и токов в этом случае будет сложнее, поскольку всегда будут присутствовать как поперечные, так и продольные составляющие полей. Такой подход исключает необходимость применения, для описания распространения электромагнитных волн, такой субстанции как эфир.
Если к рассмотренной линии бесконечной длины, или линии нагруженной волновым сопротивлением, подключить источник постоянного напряжения ![]() , то напряженность поля в линии составит:
, то напряженность поля в линии составит:
а ток, текущий в линию от источника питания, будет определяться соотношением:
(9)
Магнитное поле в линии будет равно удельному току, протекающему в линии 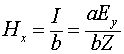 .
Подставляя сюда значение
.
Подставляя сюда значение ![]() , получаем
, получаем
(10)
Такая же связь между электрическим и магнитным полем существует и для случая поперечных электромагнитных волн, распространяющихся в свободном пространстве.
Сравнивая выражения для энергий, нетрудно видеть, что удельные энергии могут быть выражены через электрические и магнитные поля
(11)
Это означает, что удельная энергия, накопленная в магнитном и электрическом поле в такой линии одинакова. Если значения этих энергий умножить на объемы, занимаемые полями, то полученные величины совпадают с выражениями (3,4).
Таким образом, приходим к выводу, что в рассмотренной линии распространяются такие же поперечные плоские волны, как и в свободном пространстве. Причем этот вывод получен не путём решения уравнений Максвелла, а путём рассмотрения динамических процессов, которые отнесены к разряду параметрической самоиндукции. Особенностью такой линии будет то, что в ней, в отличие от свободного пространства, могут распространяться постоянные магнитные и электрические поля, а этот случай не может быть рассмотрен путем решения уравнений Максвелла.
Следовательно, условно можно считать, что длинная линия является устройством, которое при подключении к ней источника постоянного напряжения заполняется двумя видами энергии: электрической и магнитной. Удельные плотности этих энергий равны, а поскольку и электрическая и магнитная энергии заполняют одинаковые объемы, то и общая энергия, накопленная в этих полях одинакова. Особенностью данной линии является то, что при протекании в линии постоянного тока распределение электрического и магнитного полей в ней является однородным. Нетрудно показать, что сила, действующая на проводники такой линии, равна нулю. Это следует из соотношения (11), в котором его правая и левая части представляют удельные силы, приложенные к плоскостям линии. Но электрическая и магнитная силы имеют разные знаки, поэтому они компенсируют друг друга. Этот вывод касается и передающих линий любой другой конфигурации.
Если к линии приложить напряжение, меняющееся со временем по любому закону![]() , то по аналогии с (5) можно записать
, то по аналогии с (5) можно записать
(12)
Аналогичное соотношение будет и для магнитных полей.
Очевидно, что произведение ![]() представляет мощность
представляет мощность ![]() , передаваемую через поперечное сечение линии в направлении
, передаваемую через поперечное сечение линии в направлении ![]() . Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим
. Если в этом соотношении ток и напряжение заменить через напряженности магнитного и электрического полей, то получим ![]() . Произведение
. Произведение ![]() представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
представляет абсолютную величину вектора Пойнтинга, представляющего удельную мощность, передаваемую через поперечное сечение линии единичной площади. Конечно, все это можно записать и в векторной форме.
Таким образом, все выводы, полученные на основании рассмотрения процессов в длинной линии двумя методами, совпадают. Поэтому и в дальнейшем, не рискуя допустить ошибки принципиального характера, можно для описания процессов в длинных линиях с успехом пользоваться такими параметрами, как распределенная индуктивность и ёмкость. Конечно, при этом следует понимать, что ![]() и
и ![]() это некоторые интегральные характеристики, не учитывающие структуру полей.
это некоторые интегральные характеристики, не учитывающие структуру полей.
Следует отметить, что с практической точки зрения, применение параметров ![]() и
и ![]() имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.
имеет важное значение, т.к. могут быть приближенно решены задачи, которые при помощи уравнений Максвелла решить нельзя. Это, например, случай, когда проводниками передающей линии являются спирали.