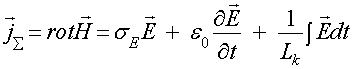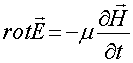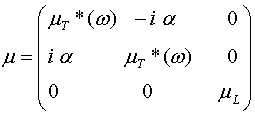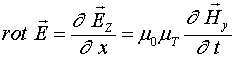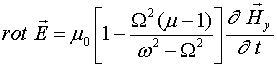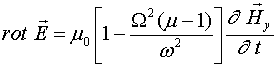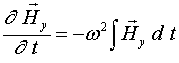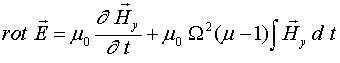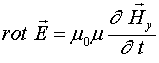Кинетическая ёмкость
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Введение
Все привыкли думать, что любое механическое движение всегда является инерционным и не может мгновенно прекратиться после снятия силы его побуждающей. Однако это не так. Прецессионное движение волчка, осуществляющего прецессионное движение в поле силы тяжести, является безинерционным и мгновенно прекращается в случае утраты опоры его оси. В этом легко убедиться, быстро убрав из под волчка его опору. При своём свободном падении волчек продолжает вращаться, однако его ось прекращает прецессию и остаётся в том положении, в котором находилась в момент потери опоры.
В электродинамике инерционные свойства заряда сопоставляют с его кинетической индуктивностью. Однако известно, что в магнитном поле атомы или молекулы, имеющие магнитный момент, тоже осуществляют прецессионное движение, которое является безинерционным и мгновенно прекращается при снятии магнитного поля. И если инерционные свойства зарядов описываются их кинетической индуктивностью, то возникает вопрос, какими параметрами описывается безинерционное прецессионное движение магнитных моментов в магнитном поле.
Кинетическая емкость
Второе уравнение Максвелла для проводящих сред имеет вид:
(1)
где ![]() - проводимость,
- проводимость, ![]() - диэлектрическая проницаемость вакуума,
- диэлектрическая проницаемость вакуума, ![]() - кинетическая индуктивность свободных зарядов.
- кинетическая индуктивность свободных зарядов.
Уравнение (1) даёт суммарную плотность тока в проводящей среде. Первое слагаемое правой части представляет резистивный ток, второе – ток смещение и третье слагаемое представляет ток проводимости.
В то же время, первое уравнение Максвелла записывается следующим образом:
где ![]() - магнитная проницаемость среды. Видно, что уравнения (1) и (2) несимметричны.
- магнитная проницаемость среды. Видно, что уравнения (1) и (2) несимметричны.
Несколько улучшить симметрию этих уравнений можно введя в уравнение (2) член линейный по магнитному полю, учитывающий тепловые потери в магнетиках в переменных полях:
где ![]() - проводимость магнитных токов. Но вот интеграла такого типа, который имеется в правой части уравнения (1), в данном уравнении нет. В то же время нам известно, что атом, обладающий магнитным моментом
- проводимость магнитных токов. Но вот интеграла такого типа, который имеется в правой части уравнения (1), в данном уравнении нет. В то же время нам известно, что атом, обладающий магнитным моментом ![]() , помещённый в магнитное поле, и осуществляющий в нём прецессионное движение, имеет потенциальную энергию
, помещённый в магнитное поле, и осуществляющий в нём прецессионное движение, имеет потенциальную энергию ![]() . Поэтому потенциальная энергия может накапливаться не только в электрических полях, а и в прецессионном движении магнитных моментов, которое не обладает инерцией. Аналогичный случай имеется и в механике, когда гироскоп, прецессирующий в поле внешних сил, накапливает потенциальную энергию. По определению механическое прецессионное движение также является безинерционным и сразу же прекращается после снятия внешних сил. Например, если из под прецессирующего волчка, вращающегося в поле земного тяготения, быстро убрать опору, то он начнёт падать, сохраняя в пространстве то направление своей оси, которое было в момент, когда была убрана опора. Такая же ситуация имеет место и для случая прецессирующего магнитного момента. Его прецессия является безинерционной и прекращается в момент снятия магнитного поля.
. Поэтому потенциальная энергия может накапливаться не только в электрических полях, а и в прецессионном движении магнитных моментов, которое не обладает инерцией. Аналогичный случай имеется и в механике, когда гироскоп, прецессирующий в поле внешних сил, накапливает потенциальную энергию. По определению механическое прецессионное движение также является безинерционным и сразу же прекращается после снятия внешних сил. Например, если из под прецессирующего волчка, вращающегося в поле земного тяготения, быстро убрать опору, то он начнёт падать, сохраняя в пространстве то направление своей оси, которое было в момент, когда была убрана опора. Такая же ситуация имеет место и для случая прецессирующего магнитного момента. Его прецессия является безинерционной и прекращается в момент снятия магнитного поля.
С учётом сказанного можно ожидать, что при описании прецессионного движения магнитного момента во внешнем магнитном поле в правой части соотношения (3) может появиться слагаемое того же типа, что и в соотношении (1). Только вместо ![]() будет стоять
будет стоять ![]() , т.е. кинетическая ёмкость, характеризующая ту потенциальную энергию, которую имеет прецессирующий магнитный момент в магнитном поле:
, т.е. кинетическая ёмкость, характеризующая ту потенциальную энергию, которую имеет прецессирующий магнитный момент в магнитном поле:
(4)
Впервые такое представление первого уравнения Максвелла с учётом кинетической ёмкости было дано в работе [1].
Посмотрим, может ли реализоваться такой случай на практике, и что из себя представляет кинетическая ёмкость. Резонансные процессы в плазме и диэлектриках характеризуются тем, что в процессе колебаний происходит попеременное преобразование электростатической энергии в кинетическую энергию движения зарядов и наоборот. Такой процесс может быть назван электрокинетическим и все устройства: лазеры, мазеры, фильтры и т.д., которые используют этот процесс, могут быть названы электрокинетическими. Наряду с этим существует и другой тип резонанса – магнитный. Если пользоваться существующими представлениями о зависимости магнитной проницаемости от частоты, то не трудно показать, что такая зависимость связана с наличием магнитного резонанса. Чтобы показать это, рассмотрим конкретный пример ферромагнитного резонанса. Если намагнитить феррит, приложив постоянное поле ![]() параллельно оси
параллельно оси ![]() , то по отношению к внешнему переменному полю среда будет выступать как анизотропный магнетик с комплексной проницаемостью в виде тензора [2]
, то по отношению к внешнему переменному полю среда будет выступать как анизотропный магнетик с комплексной проницаемостью в виде тензора [2]
где
(4)
есть собственная частота прецессии, а
(5)
есть намагниченность среды. Учитывая (4) и (5) для ![]() , можно записать
, можно записать
(6)
Получилось, что магнитная проницаемость магнетика зависит от частоты, и могут возникнуть подозрения, что, как и в случае с плазмой, здесь есть какой-то подвох.
Если считать, что электромагнитная волна распространяется вдоль оси ![]() и имеются компоненты полей
и имеются компоненты полей ![]() и
и ![]() , то первое уравнение Максвелла примет вид:
, то первое уравнение Максвелла примет вид:
Учитывая (6), получим
(7)
Полагая ![]() и учитывая, что в этом случае
и учитывая, что в этом случае
из (7) получаем
или
(8)
Для случая ω<<Ω находим
Величину
которая введена в соотношении (8) назовем кинетической емкостью.
С чем связано существование этого параметра, и каков его физический смысл? Если направление магнитного момента не совпадает с направлением внешнего магнитного поля, то вектор такого момента начинает прецессировать вокруг вектора магнитного поля с частотой Ω. Магнитный момент ![]() обладает при этом потенциальной энергией
обладает при этом потенциальной энергией ![]() . Эта энергия подобно энергии заряженного конденсатора является потенциальной, потому что прецессионное движение, хотя и является механическим, однако, оно безинерционно и мгновенно прекращается при снятии магнитного поля. При наличии же магнитного поля прецессионное движение продолжается до тех пор, пока не будет израсходована накопленная потенциальная энергия, и вектор магнитного момента не станет параллельным вектору магнитного поля.
. Эта энергия подобно энергии заряженного конденсатора является потенциальной, потому что прецессионное движение, хотя и является механическим, однако, оно безинерционно и мгновенно прекращается при снятии магнитного поля. При наличии же магнитного поля прецессионное движение продолжается до тех пор, пока не будет израсходована накопленная потенциальная энергия, и вектор магнитного момента не станет параллельным вектору магнитного поля.
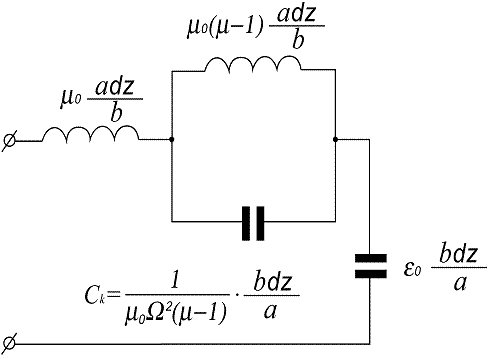
Эквивалентная схема рассмотренного случая приведена на рис. 1. В точке ![]() =Ω имеет место магнитный резонанс, при этом μτ*(ω)→ − бесконечность. Резонансная частота макроскопического магнитного резонатора, как легко видеть из эквивалентной схемы, также не зависит от размеров линии и равна Ω. Таким образом, параметр
=Ω имеет место магнитный резонанс, при этом μτ*(ω)→ − бесконечность. Резонансная частота макроскопического магнитного резонатора, как легко видеть из эквивалентной схемы, также не зависит от размеров линии и равна Ω. Таким образом, параметр
не является частотно зависимой магнитной проницаемостью, а включает в себя m0, m и Сk, которые включены в соответствии с эквивалентной схемой, изображенной на рис. 1.
Нетрудно показать, что в данном случае имеет место распространение трех волн: электрической, магнитной и волны, несущей потенциальную энергию, которая связана с прецессией магнитных моментов вокруг вектора ![]() .
.
Рис. 1. Эквивалентная схема двухпроводной линии, заполненной магнетиком.
По этой причине такие волны могут быть названы электромагнитнопотенциальными. Все устройства, в которых используются такие волны, также могут быть названы электромагнитнопотенциальными.
До появления работы [1] в электродинамике такое понятие, как кинетическая ёмкость не использовалось, хотя это реальный параметр имеет очень понятную физическую интерпретацию.
Литература
- 1. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 2. Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн. М: Наука, 1989.- 543 с.