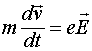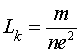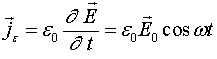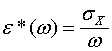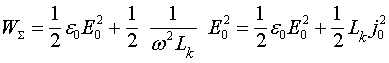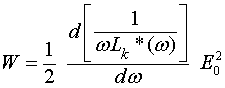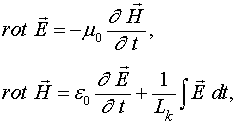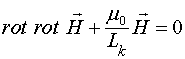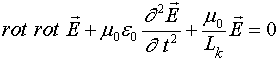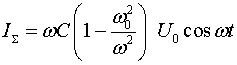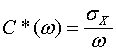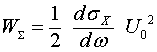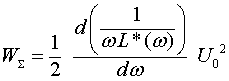Как Ландау перепутал интеграл гармонической функции с её производной
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Казалось бы, такая мелочь, всего то знаком отличается интеграл гармонической функции от её производной. Это уже даже школьникам известно. Но забыл Ландау об этом, и с его подачи эта мелочь всю физику вверх дном перевернула. А дело было так. Открываем работу [1], и нас сразу удивляет тот факт, что в девятой главе, где начинается рассмотрение диэлектриков в переменных электрических полях, не вводится понятие диэлектрической проницаемости среды в таких полях (это понятие мы введём ниже). Дальше хуже. В §78 вводится диэлектрическая проницаемость проводников и диэлектриков на больших частотах. При этом утверждается, что на очень высоких частотах нет никакой разницы между диэлектриками и проводниками, и используется следующая методика (далее все соотношения будут записываться в системе СИ). Записывается уравнение движения для свободного заряда
(1)
и находится его смещение при воздействии переменного электрического поля
Затем говорится, что поляризация ![]() есть дипольный момент единицы объёма, и полученное значение смещения вводится в поляризацию
есть дипольный момент единицы объёма, и полученное значение смещения вводится в поляризацию
В данном случае рассматривается точечный заряд, и эта операция означает введение электрического дипольного момента для двух точечных зарядов с противоположными знаками, расположенными на расстоянии ![]()
Этот шаг вызывает недоумение, поскольку рассматривается газ свободных электронов, но чтобы говорить об электрическом дипольном моменте, нужно иметь в этой среде для каждого электрона заряд противоположного знака, отнесённый от него на расстояние ![]() . Такой подход верен для диэлектриков, где заряды связаны. В данном же случае рассматривается газ свободных электронов, в котором отсутствуют заряды противоположных знаков. Далее следует стандартная процедура, когда введённый таким незаконным способом вектор поляризации вводится в диэлектрическую проницаемость
. Такой подход верен для диэлектриков, где заряды связаны. В данном же случае рассматривается газ свободных электронов, в котором отсутствуют заряды противоположных знаков. Далее следует стандартная процедура, когда введённый таким незаконным способом вектор поляризации вводится в диэлектрическую проницаемость
а поскольку плазменная частота определяется соотношением
сразу записывается вектор индукции
При таком подходе получается, что коэффициент пропорциональности между электрическим полем и электрической индукцией
называемый Ландау диэлектрической проницаемостью, зависит от частоты.
Именно такой подход и привёл к тому, что все начали считать, что величина, стоящая в этом соотношении перед вектором электрического поля, есть зависящая от частоты диэлектрическая проницаемость, и электрическая индукция, в свою очередь, тоже зависит от частоты. И об этом говорится во всех, без исключения, фундаментальных работах по электродинамике материальных сред.
Теперь покажем, как нужно правильно рассматривать этот вопрос. Используя выражение для плотности тока
(2)
из (1) получаем ток проводимости
(3)
В соотношении (2) и (3) величина ![]() представляет плотность электронов. Введя обозначение
представляет плотность электронов. Введя обозначение
(4)
находим
(5)
В данном случае величина ![]() представляет удельную кинетическую индуктивность носителей заряда [2-6]. Ее существование связано с тем, что заряд, имея массу, обладает инерционными свойствами. Для случая гармонических полей
представляет удельную кинетическую индуктивность носителей заряда [2-6]. Ее существование связано с тем, что заряд, имея массу, обладает инерционными свойствами. Для случая гармонических полей ![]() соотношение (5) запишется:
соотношение (5) запишется:
(6)
Из соотношения (5) и (6) видно, что ![]() представляет индуктивный ток, т.к. его фаза запаздывает по отношению к напряжённости электрического поля на угол
представляет индуктивный ток, т.к. его фаза запаздывает по отношению к напряжённости электрического поля на угол ![]() .
.
Если рассматриваемые электроны находятся в вакууме, то при нахождении суммарного тока нужно учитывать и ток смещения
Видно, что этот ток носит ёмкостной характер, т.к. его фаза на ![]() опережает фазу напряжённости электрического поля. Таким образом, суммарная плотность тока составит [2]:
опережает фазу напряжённости электрического поля. Таким образом, суммарная плотность тока составит [2]:
Или
(7)
В соотношении (7) величина, стоящая в скобках, представляет суммарную реактивную проводимость данной среды ![]() и состоит, в свою очередь, из емкостной
и состоит, в свою очередь, из емкостной ![]() и индуктивной
и индуктивной ![]() проводимости
проводимости
Соотношение (7) можно переписать и по-другому:
где 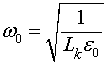 - плазменная частота плазменных колебаний.
- плазменная частота плазменных колебаний.
И здесь возникает большой соблазн назвать величину
(8)
зависящей от частоты диэлектрической проницаемостью плазмы, что и делает Ландау. Но это неправильно, т.к. данный математический символ является сборным параметром, в который одновременно входит диэлектрическая проницаемость вакуума и удельная кинетическая индуктивность зарядов. Записав соотношение (8) Ландау ввёл в один коэффициент одновременно и производную и интеграл гармонической функции. При этом производная представляет реактивный ток смещения в проводнике и определяется диэлектрической проницаемостью вакуума, а интеграл определяет реактивный ток проводимости и определяется кинетической индуктивностью носителей зарядов.
С целью дальнейшей конкретизации рассмотрения вопросов дисперсии введём определение понятия диэлектрической проницаемости среды для случая переменных полей.
Если рассмотреть любую среду, в том числе и плазму, то плотность токов (в дальнейшем будем сокращённо говорить просто ток) будет определяться тремя составляющими, зависящими от электрического поля. Ток резистивных потерь будет синфазен электрическому полю. Ёмкостной ток, определяемый первой производной электрического поля по времени, будет опережать напряженность электрического поля по фазе на ![]() . Этот ток называется током смещения. Ток проводимости, определяемый интегралом от электрического поля по времени, будет опережать электрическое поле по фазе на
. Этот ток называется током смещения. Ток проводимости, определяемый интегралом от электрического поля по времени, будет опережать электрическое поле по фазе на ![]() . Все три указанные составляющие тока и будут входить во второе уравнение Максвелла и других составляющих токов быть не может. Причём все эти три составляющие токов в обязательном порядке будут присутствовать в любых немагнитных средах. Поэтому вполне естественно, диэлектрическую проницаемость любой среды определить как коэффициент, стоящий перед тем членом, который определяется производной электрического поля по времени во втором уравнении Максвелла. При этом следует учесть, что диэлектрическая проницаемость не может быть отрицательной величиной. Это связано с тем, что через этот параметр определяется энергия электрических полей, которая может быть только положительной.
. Все три указанные составляющие тока и будут входить во второе уравнение Максвелла и других составляющих токов быть не может. Причём все эти три составляющие токов в обязательном порядке будут присутствовать в любых немагнитных средах. Поэтому вполне естественно, диэлектрическую проницаемость любой среды определить как коэффициент, стоящий перед тем членом, который определяется производной электрического поля по времени во втором уравнении Максвелла. При этом следует учесть, что диэлектрическая проницаемость не может быть отрицательной величиной. Это связано с тем, что через этот параметр определяется энергия электрических полей, которая может быть только положительной.
Не введя такого чёткого определения диэлектрической проницаемости, Ландау и начинает рассмотрение поведения плазмы в переменных электрических полях. При этом он не выписывает отдельно ток смещения и ток проводимости, один из которых определяется производной, а другой интегралом, а сваливает эти два тока в одну кучу, вводя диэлектрическую проницаемость плазмы. Делает он это по той причине, что в случае гармонических колебаний вид функции, определяющей и производную и интеграл, одинаков, а отличаются функции лишь знаком. Производя такую операцию, Ландау не понимает, что в случае гармонических электрических полей в плазме существуют два различных тока, один из которых является током смещения, и определяется диэлектрической проницаемостью вакуума и производной от электрического поля. Другой ток является током проводимости и определяется удельной кинетической индуктивностью и интегралом от электрического поля. Причём эти два тока противофазны. А поскольку оба тока зависят от частоты, причём один из них зависит от частоты линейно, а другой обратно пропорционально частоте, то между ними имеет место конкуренция. При низких частотах преобладает ток проводимости, при высоких, наоборот, преобладает ток смещения. В случае же равенства этих токов, что имеет место на плазменной частоте, имеет место резонанс токов.
Подчеркнём, что в принципе, с математической точки зрения, так как поступил Ландау, поступать можно, но при этом теряется постоянная интегрирования, которая необходима для учёта начальных условий при решении интегродифференциального уравнения, определяющего плотность тока в материальной среде.
Верна и другая точка зрения. Соотношение (7) можно переписать и по-другому:
и ввести другой математический символ
В данном случае также возникает соблазн назвать эту величину зависящей от частоты кинетической индуктивностью. Но эту величину называть индуктивностью тоже нельзя, поскольку это также сборный параметр, который включает в себя не зависящие от частоты кинетическую индуктивность и диэлектрическую проницаемость вакуума.
Таким образом, можно записать:
или
Но это всего лишь символическая математическая запись одного и того же соотношения (7). Оба уравнения эквивалентны, и по отдельности математически полностью характеризуют рассмотренную среду. Но с физической точки зрения ни ![]() , ни
, ни ![]() диэлектрической проницаемостью или индуктивностью не являются. Физический смысл их названий заключается в следующем:
диэлектрической проницаемостью или индуктивностью не являются. Физический смысл их названий заключается в следующем:
т.е. ![]() представляет суммарную реактивную проводимость среды, деленную на частоту, а
представляет суммарную реактивную проводимость среды, деленную на частоту, а
представляет обратную величину произведения реактивной проводимости на частоту.
Как нужно поступать, если в нашем распоряжении имеются величины ![]() и
и ![]() , а нам необходимо вычислить полную энергию, заключённую в единице объёма. Естественно подставлять эти величины в формулы, определяющие энергию электрических полей
, а нам необходимо вычислить полную энергию, заключённую в единице объёма. Естественно подставлять эти величины в формулы, определяющие энергию электрических полей
и кинетическую энергию носителей зарядов
(9)
нельзя, просто потому, что эти параметры не являются ни диэлектрической проницаемостью, ни индуктивностью. Нетрудно показать, что в этом случае полная энергия, заключённая в единице объёма, может быть получена из соотношения
(10)
откуда получаем
Тот же результат получим, воспользовавшись формулой
Приведенные соотношения показывают, что энергия, заключённая в единичном объёме проводника состоит из потенциальной энергии электрических полей и кинетической энергии носителей зарядов.
При рассмотрении любых сред нашей конечной задачей является нахождение волнового уравнения. В данном случае эта задача уже практически решена. Уравнения Максвелла для этого случая имеют вид:
(11)
где ![]() и
и ![]() – диэлектрическая и магнитная проницаемость вакуума.
– диэлектрическая и магнитная проницаемость вакуума.
Система уравнений (11) полностью описывает все свойства проводников. Из неё получаем
(12)
Для случая полей, не зависящих от времени, уравнение (12) переходит в уравнение Лондонов
где 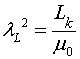 – лондоновская глубина проникновения.
– лондоновская глубина проникновения.
Таким образом, можно заключить, что уравнения Лондонов являясь частным случаем уравнения (12), и не учитывают токов смещения в среде. Поэтому они не дают возможности получить волновые уравнения, описывающие процессы распространения электромагнитных волн в сверхпроводниках.
Для электрических полей волновое уравнение в этом случае выглядит следующим образом:
Для постоянных полей можно записать
Следовательно, постоянные электрические поля проникают в сверхпроводник таким же образом, как и магнитные, убывая по экспоненциальному закону. Плотность же тока при этом растёт по линейному закону
Проведенное рассмотрение показало, что диэлектрическая проницаемость проводников и плазмы равна диэлектрической проницаемости вакуума и эта проницаемость от частоты не зависит. Этому параметру обязано накопление в плазме потенциальной энергии. Кроме того, такую среду характеризует ещё и кинетическая индуктивность носителей зарядов и этот параметр ответственен за накопление в плазме кинетической энергии.
Таким образом, получены все необходимые характеристики, характеризующие процесс распространения электромагнитных волн в рассмотренных проводящих средах. Однако в отличие от общепринятой методики [1] при таком рассмотрении нигде не вводился вектор поляризации, а в основу рассмотрения положено уравнение движения и при этом во втором уравнении Максвелла выписываются все составляющие плотностей токов в явном виде.
В радиотехнике существует простой метод представления радиотехнических элементов и материальных сред при помощи эквивалентных схем. Этот метод является очень наглядным и даёт возможность представлять в виде таких схем элементы, как с сосредоточенными, так и с распределёнными параметрами. Использование этого метода позволяет нам лучше понять, почему были допущены такие существенные физические ошибки в работе Ландау при введении понятия зависящей от частоты диэлектрическая проницаемость плазмы.
Чтобы показать, что единичный объём проводника или плазмы по своим электродинамическим характеристикам эквивалентен параллельному резонансному контуру с сосредоточенными параметрами, рассмотрим параллельный резонансный контур, когда емкость ![]() и индуктивность
и индуктивность ![]() включены параллельно. Связь между напряжением
включены параллельно. Связь между напряжением ![]() , приложенным к контуру, и суммарным током
, приложенным к контуру, и суммарным током ![]() , текущем через такую цепь, имеет вид
, текущем через такую цепь, имеет вид
где  – ток, текущий через емкость, а
– ток, текущий через емкость, а  – ток, текущий через индуктивность.
– ток, текущий через индуктивность.
Для случая гармонического напряжения ![]() получаем
получаем
(13)
Величина, стоящая в скобках, представляет суммарную реактивную проводимость ![]() рассмотренной цепи и состоит, в свою очередь, из емкостной
рассмотренной цепи и состоит, в свою очередь, из емкостной ![]() и индуктивной
и индуктивной ![]() проводимости
проводимости
Соотношение (13) можно переписать следующим образом:
где 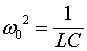 – резонансная частота параллельного контура.
– резонансная частота параллельного контура.
И здесь, также как и в случае плазмы, возникает соблазн, назвать величину
(14)
зависящей от частоты ёмкостью. С математической (подчеркиваю, с математической, но не с физической) точки зрения ведении такого символа совершенно естественно, однако недопустимым является присвоение ему предлагаемого названия, т.к. этот параметр никакого отношения к истинной ёмкости не имеет и включает в себя одновременно и ёмкость и индуктивность контура, которые от частоты не зависят.
Верна и другая точка зрения. Соотношение (13) можно переписать и по-другому:
и считать, что рассматриваемая цепь вообще не имеет емкости, а состоит только из зависящей от частоты индуктивности
(15)
Но, так же как и ![]() , величину
, величину ![]() называть индуктивностью нельзя, поскольку это тоже сборный параметр, включающий в себя одновременно ёмкость и индуктивность, которые от частоты не зависят.
называть индуктивностью нельзя, поскольку это тоже сборный параметр, включающий в себя одновременно ёмкость и индуктивность, которые от частоты не зависят.
Используя выражения (14) и (15), запишем:
(16)
или
(17)
Соотношения (16) и (17) эквивалентны, и по отдельности математически полностью характеризуют рассмотренную цепь. Но с физической точки зрения ни ![]() , ни
, ни ![]() емкостью и индуктивностью не являются, хотя и имеют ту же размерность. Физический смысл их названий заключается в следующем:
емкостью и индуктивностью не являются, хотя и имеют ту же размерность. Физический смысл их названий заключается в следующем:
т.е. ![]() представляет суммарную реактивную проводимость данной цепи, деленную на частоту, а
представляет суммарную реактивную проводимость данной цепи, деленную на частоту, а
является обратной величиной произведения суммарной реактивной проводимости на частоту.
Накапливаемая в ёмкости и индуктивности энергия, определяется из соотношений
(18)
(19)
Каким образом следует поступать для вычисления энергии, накопившейся в контуре, если в нашем распоряжении имеются ![]() и
и ![]() ? Конечно, вставлять эти соотношения в формулы (18) и (19) нельзя уже хотя бы потому, что эти величины могут быть как положительными, так и отрицательными, а энергия, накопившаяся в емкости и индуктивности, всегда положительна. Но если для этих целей пользоваться указанными параметрами, то нетрудно показать, что суммарная энергия, накопленная в контуре, определяется выражениями:
? Конечно, вставлять эти соотношения в формулы (18) и (19) нельзя уже хотя бы потому, что эти величины могут быть как положительными, так и отрицательными, а энергия, накопившаяся в емкости и индуктивности, всегда положительна. Но если для этих целей пользоваться указанными параметрами, то нетрудно показать, что суммарная энергия, накопленная в контуре, определяется выражениями:
(20)
или
(21)
или
(22)
Если расписать уравнения (2.19) или (2.20) и (2.21), то получим одинаковый результат, а именно:
где ![]() – есть амплитуда напряжения на ёмкости, а
– есть амплитуда напряжения на ёмкости, а ![]() – амплитуда тока, текущего через индуктивность.
– амплитуда тока, текущего через индуктивность.
Если сравнить соотношения, полученные для параллельного резонансного контура и для проводников, то можно видеть, что они идентичны, если сделать замену ![]() ,
, ![]() ,
, ![]() и
и ![]() . Таким образом, единичный объём проводника, при однородном распределении электрических полей и плотностей токов в нём, эквивалентен параллельному резонансному контуру с указанными сосредоточенными параметрами. При этом ёмкость такого контура численно равна диэлектрической проницаемости вакуума, а индуктивность равна удельной кинетической индуктивности.
. Таким образом, единичный объём проводника, при однородном распределении электрических полей и плотностей токов в нём, эквивалентен параллельному резонансному контуру с указанными сосредоточенными параметрами. При этом ёмкость такого контура численно равна диэлектрической проницаемости вакуума, а индуктивность равна удельной кинетической индуктивности.
А теперь представим себе такую ситуацию. В аудиторию, где находятся специалисты, знающие радиотехнику, с одной стороны, и математики – с другой, приходит преподаватель и начинает доказывать, что нет в природе никаких индуктивностей, а существует только зависящая от частоты ёмкость и что она-то и представляет параллельный резонансный контур. Или, наоборот, что параллельный резонансный контур это зависящая от частоты индуктивность. С такой точкой зрения математики сразу согласятся. Однако радиотехники посчитают лектора человеком с очень ограниченными знаниями. Именно в таком положении оказались сейчас те учёные и специалисты, которые ввели в физику частотную дисперсию диэлектрической проницаемости.
Примечания
Литература
- Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- Менде Ф. Ф., Спицын А. И. Поверхностный импеданс сверхпроводников. Киев, Наукова думка, 1985.- 240 с.
- Mende F. F. Transversal plasma resonance in a nonmagnetized plasma and possibilities of practical employment of it. arXiv, physics/0506081.