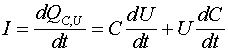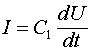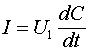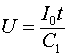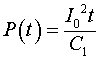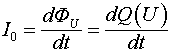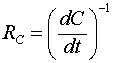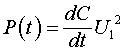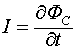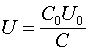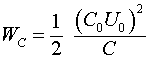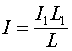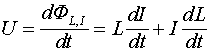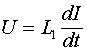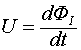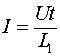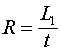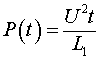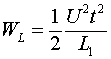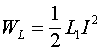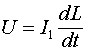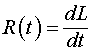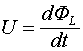Законы самоиндукции
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: | |
Введение
К законам самоиндукции следует отнести те законы, которые описывают реакцию таких элементов радиотехнических цепей, как ёмкость, индуктивность и сопротивление при гальваническом подключении к ним источников тока или напряжения. Эти законы являются основой теории электрических цепей. Результаты этой теории в отдельных случаях могут быть перенесены и на электродинамику материальных сред, т.к. такие среды могут быть представлены в виде эквивалентных схем с использованием таких элементов.
Движение или накопление зарядов в какой-либо цепи связано с потреблением энергии от источников питания, которые заставляют их менять своё местоположение или двигаться. Процессы взаимодействия источников питания с такими структурами регулируются законами самоиндукции.
Еще раз уточним само понятие самоиндукции. Под самоиндукцией будем понимать реакцию радиотехнических элементов с неизменными параметрами на подключение к ним источников напряжения или тока. К самоиндукции отнесём также тот случай, когда при наличии подключенного источника питания или накопленной в системе энергии могут меняться ее параметры. Такую самоиндукцию будем называть параметрической. В дальнейшем будем использовать такие понятия: как генератор тока и генератор напряжения. Под идеальным генератором напряжения будем понимать такой источник, который обеспечивает на любой нагрузке заданное напряжение, внутреннее сопротивление у такого генератора равно нулю. Под идеальным генератором тока будем понимать такой источник, который обеспечивает в любой нагрузке заданный ток, внутреннее сопротивление у такого генератора равно бесконечности. Идеальных генераторов тока и напряжения в природе не существует, поскольку и генераторы тока и генераторы напряжения имеют свое внутреннее сопротивление, которое и ограничивает их возможности.
Если к тому или другому элементу цепи подключить генератор тока или напряжения, то ответной реакцией такого элемента является противодействие изменению своего начального состояния и это противодействие всегда равно приложенному действию, что соответствует третьему закону Ньютона.
Ёмкостная самоиндукция
Если в нашем распоряжении имеется емкость ![]() , и эта емкость заряжена до разности потенциалов
, и эта емкость заряжена до разности потенциалов ![]() , то заряд
, то заряд ![]() , накопленный в емкости, определяется соотношением:
, накопленный в емкости, определяется соотношением:
Заряд ![]() , зависящий от величины ёмкости конденсатора и от разности потенциалов на нём, будем называть ещё потоком ёмкостной самоиндукции.
, зависящий от величины ёмкости конденсатора и от разности потенциалов на нём, будем называть ещё потоком ёмкостной самоиндукции.
Когда речь идет об изменении заряда, определяемого соотношением (2.1), то эта величина может изменяться путем изменения разности потенциалов при постоянной емкости, или изменением самой емкости при постоянной разности потенциалов, или и того и другого параметра одновременно.
Если величина емкости или разности потенциалов на ёмкости зависят от времени, то величина тока определяется соотношением:
Это выражение определяет закон ёмкостной самоиндукции. Таким образом, ток в цепи, содержащей конденсатор, можно получить двумя способами, изменяя напряжение на конденсаторе при постоянной его ёмкости или изменяя саму ёмкость при неизменном напряжении на конденсаторе, или производить изменение обоих параметров одновременно.
Для случая, когда емкость ![]() постоянна, получаем известное выражение для тока, текущего через емкость:
постоянна, получаем известное выражение для тока, текущего через емкость:
В том случае, если изменяется емкость, и на ней поддерживается неизменное напряжение ![]() , имеем:
, имеем:
Этот случай относиться к параметрической ёмкостной самоиндукции поскольку наличие тока связано с изменением такого параметра как ёмкость.
Рассмотрим следствия, вытекающие из соотношения (2.2).
Если к емкости подключить генератор постоянного тока ![]() , то напряжение на ней будет изменяться по закону:
, то напряжение на ней будет изменяться по закону:
Таким образом, емкость, подключенная к источнику постоянного тока, представляет для него активное сопротивление
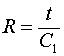 (2.5)
(2.5)
которое линейно зависит от времени. Следует отметить, что полученный результат является вполне очевидным, однако такие свойства ёмкости, которую принято считать реактивным элементом впервые были отмечены в работе [1].
С физической точки зрения это понятно, т.к., чтобы заряжать емкость, источник должен расходовать энергию.
Мощность, отдаваемая источником тока, определяется в данном случае соотношением:
Энергию, накопленную емкостью за время ![]() , получим, проинтегрировав соотношение (2.6) по времени:
, получим, проинтегрировав соотношение (2.6) по времени:
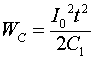 Подставляя сюда значение тока из соотношения (2.4), получаем зависимость величины накопленной в емкости энергии от текущего значения напряжения на ней:
Подставляя сюда значение тока из соотношения (2.4), получаем зависимость величины накопленной в емкости энергии от текущего значения напряжения на ней:
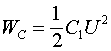 Используя для рассмотренного случая понятие потока электрической индукции
Используя для рассмотренного случая понятие потока электрической индукции
и используя соотношение (2.2), получаем:
т.е., если к постоянной емкости подключить источник постоянного тока, то величина тока будет равна производной потока ёмкостной индукции по времени.
Теперь будем поддерживать на емкости постоянное напряжение ![]() , а изменять саму ёмкость, тогда
, а изменять саму ёмкость, тогда
(2.9)
Видно, что величина
играет роль активного сопротивления. Этот результат тоже физически понятен, т.к. при увеличении емкости увеличивается накопленная в ней энергия, и таким образом, ёмкость отбирает у источника напряжения энергию, представляя для него активную нагрузку. Мощность, расходуемая при этом источником, определяется соотношением:
Из соотношения (2.11) видно, что в зависимости от знака производной расходуемая мощность может иметь разные знаки. Когда производная положительная, расходуемая мощность идёт на совершение внешней работы. Если производная отрицательная, то работу совершает внешний источник.
Опять, вводя понятие поток ёмкостной индукции
Соотношения (2.8) и (2.12) указывают на то, что независимо от того, каким способом изменяется поток, его производная по времени всегда равна току.
Рассмотрим еще один процесс, который ранее к законам индукции не относили, однако, он подпадает под наше расширенное определение этого понятия. Из соотношения (2.7) видно, что если поток, т.е. заряд, оставить неизменным (будем называть этот режим режимом замороженного ёмкостного потока, или замороженного заряда), то напряжение на емкости можно изменять путем ее изменения. В этом случае будет выполняться соотношение:
где ![]() и
и ![]() - текущие значения, а
- текущие значения, а ![]() и
и ![]() - начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
Напряжение на емкости и энергия, накопленная в ней, будут при этом определяться соотношениями:
- начальные значения этих параметров, имеющие место при отключении от емкости источника питания.
Напряжение на емкости и энергия, накопленная в ней, будут при этом определяться соотношениями:
(2.13)
Естественно, что данный процесс самоиндукции может быть связан только с изменением самой емкости, и поэтому он подпадает под определение параметрической самоиндукции.
Таким образом, имеются три соотношения (2.8), (2.12) и (2.13), которые определяют процессы ёмкостной самоиндукции. Будем называть их правилами ёмкостного потока. Соотношение (2.8) определяет ёмкостную самоиндукцию, при которой отсутствуют изменения емкости, и поэтому эта самоиндукция может быть названа просто ёмкостной самоиндукцией. Соотношения (2.3) и (2.9–2.11) предполагают наличие изменений емкости, поэтому процессы, соответствующие этими соотношениями, будем называть ёмкостной параметрической самоиндукцией.
Индуктивная самоиндукция
Перейдем теперь к рассмотрению процессов, происходящих в индуктивности. Введем понятие потока индуктивной самоиндукции
Если индуктивность закорочена, и выполнена из материала, не имеющего активного сопротивления, например из сверхпроводника, то
![]() где
где ![]() и
и ![]() - какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
- какие-то начальные значения этих параметров, которые имеются в момент короткого замыкания индуктивности при наличии в ней тока.
Этот режим будем называть режимом замороженного тока. При этом выполняется соотношение:
(3.1)
В рассмотренном режиме поток индукции остается неизменным, однако, в связи с тем, что ток в индуктивности может изменяться при ее изменении, такой процесс подпадает под определение параметрической самоиндукции. Энергия, накопленная в индуктивности, при этом будет определяться соотношением
Напряжение на индуктивности, равно производной потока индуктивной индукции по времени:
Рассмотрим случай, когда индуктивность ![]() постоянна, тогда
постоянна, тогда
(3.2)
Проинтегрировав выражение (3.2) по времени, получим:
Таким образом, индуктивность, подключенная к источнику постоянного напряжения, представляет для него активное сопротивление
(3.4)
которое уменьшается обратно пропорционально времени. Мощность, расходуемая при этом источником, определится соотношением:
(3.5)
Эта мощность линейно зависит от времени. Проинтегрировав соотношение (3.5) по времени, получим энергию, накопленную в индуктивности
(3.6)
Подставив в выражение (3.6) значение напряжения из соотношения (3.3), получаем:
Эта энергия может быть возвращена из индуктивности во внешнюю цепь, если индуктивность отключить от источника питания и подключить к ней активное сопротивление.
Теперь рассмотрим случай, когда ток ![]() , протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
, протекающий через индуктивность, постоянен, а сама индуктивность может изменяться. В этом случае получаем соотношение
(3.7)
Таким образом, величина
(3.8)
играет роль активного сопротивления.
Как и в случае электрического потока, активное сопротивление может быть (в зависимости от знака производной), как положительным, так и отрицательным. Это означает, что индуктивность может, как получать энергию извне, так и отдавать её.
Вводя обозначение ![]() и, учитывая (3.7), получаем:
и, учитывая (3.7), получаем:
(3.9)
Соотношения (3.1), (3.6) и (3.9) будем называть правилами индуктивной самоиндукции, или правилами потока индуктивной самоиндукции. Из соотношений (3.6) и (3.9) видно, что, как и в случае с ёмкостным потоком, способ изменения индуктивного потока не влияет на конечный результат, и его производная по времени всегда равна приложенной разности потенциалов. Соотношение (3.6) определяет индуктивную самоиндукцию, при которой отсутствуют изменения индуктивности, и поэтому она может быть названа просто индуктивной самоиндукцией. Соотношения (3.7,3.8) предполагают наличие изменений индуктивности, поэтому процессы, описываемые этими соотношениями, будем называть индуктивной параметрической самоиндукцией.
Литература
- 1. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5