Задача о вращающемся волчке: постановка, решение, приложения
| Петров Анатолий Михайлович | |
| Дата рождения: |
07.09.1937 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Учёное звание: |
старший научный сотрудник |
- Задача, поставленная Эйлером 250 лет назад, не имела общего решения из-за неадекватности общепринятой методологии замкнутых систем и векторно-тензорного математического аппарата
- «Говори, что знаешь,
- делай, что должен,
- пусть будет, чему быть!»
- Девиз конкурсной работы С.В.Ковалевской, лауреата премии 1889 года Парижской академии за исследование о вращении тяжёлого несимметричного волчка
Содержание
Кратко об истории вопроса
Существует некая историческая загадка в том, почему Л.Эйлер, будучи уже, по сути, знакóм с наиболее подходящим для описания вращений математическим аппаратом (получившим в середине ХIХ века название кватернионов), тем не менее, осуществил постановку задачи о вращающемся волчке (и потом безуспешно пытался решать эту задачу) в терминах упрощённого варианта того же аппарата, который к концу ХIХ века идейно оформился в самостоятельный раздел математики под названием векторной алгебры, а затем (не без влияния авторитета Эйлера!) полностью вытеснил из теоретической физики породившее этот аппарат исчисление кватернионов.
Выдающиеся математики прошлого: Жозеф Лагранж, Луи Пуансо, Шарль Эрмит, Гастон Дарбу, а из наших соотечественников С.В.Ковалевская и Н.Е.Жуковский, – посвятили заметную (некоторые – значительную) часть своего научного творчества задаче о вращающемся волчке, не подвергая, однако, сомнению математическую корректность эйлеровой постановки задачи. Ими были получены достаточно интересные в математическом отношении результаты на пути к решению поставленной Эйлером проблемы, однако адекватного решения задачи о волчке никому найти не удалось (Оникийчук В.Н. Великая тайна Леонарда Эйлера. – СПб.: НПО «Профессионал», 2007). Впрочем, факт отсутствия адекватного решения задачи о вращающемся волчке «официальная» наука оспаривает: мол, если нет общего аналитического решения задачи, то можно воспользоваться приближёнными методами вычислений, благо компьютерная техника достаточно развита и продолжает совершенствоваться. К тому же, аналитическое решение как таковое может и не потребоваться, когда проведено «качественное исследование» задачи.
.«Задача о движении твёрдого тела вокруг неподвижной точки занимает исключительное место в динамике. В этой области работали такие выдающиеся учёные, как Л.Эйлер, Ж.Лагранж, С. Пуассон, Ж.Лиувилль, К.Якоби, Г.Дарбу и многие другие. Важные результаты в этой области были получены русскими учёными С.В.Ковалевской, Н.Е.Жуковским, С.А.Чаплыгиным, В.А.Стекловым, A.M.Ляпуновым и др. Основные их достижения относятся к концу 19-го и началу 20-го века. В настоящее время по-прежнему не ослабевает интерес к этой задаче, так как разработаны современные методы для явного интегрирования уравнений и их топологического анализа. Задача о движении твёрдого тела привлекала внимание крупнейших математиков. Дело в том, что движение тела описывается системой обыкновенных нелинейных дифференциальных уравнений, так называемыми уравнениями Эйлера-Пуассона, для которой известны только три общих интеграла. Кроме того, Якоби доказана теорема, которая показывает, что для сведения задачи к квадратурам достаточно найти ещё один новый первый интеграл, не зависящий от времени. На поиск этого дополнительного интеграла потрачено немало сил. В некоторых специальных случаях удалось найти дополнительный интеграл, но до сих пор исследования в этом направлении продолжаются. Наглядное представление о движении твёрдого тела с помощью решений уравнений Эйлера-Пуассона оказалось трудным, так как эти решения обычно выражаются достаточно сложно. Поэтому большое значение имеет качественное исследование задачи о движении твёрдого тела»— [1]
Примечательно, что исследования в данной области в течение двух с половиной веков развивались не в направлении более глубокого и точного уяснения и отражения физической сути изучаемого явления, а исключительно в сторону развития (как правило, усложнения) некогда выбранного Эйлером математического инструментария. И даже разумность такого подхода обосновывается довольно курьёзным, однако негласно разделяемым некоторыми исследователями, «научным объяснением» причины и сущности гироскопического эффекта: оказывается, волчок и гироскоп ведут себя не каким-то иным, а именно наглядно демонстрируемым образом, потому что таковы законы векторной алгебры, описывающей их поведение!
Но, на деле, пока более надёжным, чем уравнения движения волчка, источником информации об особенностях гироскопического эффекта (в первую очередь, о направлении прецессии волчка) остаётся мнемоническое правило, сформулированное "отцом русской авиации" Н.Е.Жуковским, изучавшим также механику волчков и гироскопов: гироскопический момент стремится совместить вектор кинетического момента с вектором момента действующих физических сил по кратчайшему пути. А вот даже толково и просто объяснить, почему так происходит (т.е. раскрыть физический смысл явления) наука не может!
Заметим, что в теоретической физике такое положение вещей не является чем-то исключительным: аналогичным образом в электродинамике максвелловы уравнения, «переведённые» (точнее, редуцированные) с языка кватернионов на язык векторно-тензорной алгебры и утратившие, в результате этой операции, существенную часть своего физического содержания, не определяют, а, наоборот, «опираются» на выведенное из опыта мнемоническое «правило левой руки», указывающее направление движения электрического заряда в магнитном поле.
Так и сохраняют право на жизнь в современной науке «псевдорешения» научных проблем, как правило, разделяемые на три (с различным целевым назначением и не обязательно согласующиеся друг с другом) части: одна – для общения «посвящённых в тайну» учёных на понятном только им символическом языке, другая – для приближённых инженерно-технических расчётов, а третья – для широкого распространения и использования в системе общественного образования и просвещения. Причём, если бы проблема была действительно решена, то между этими частями не возникало бы наблюдаемых сегодня «барьеров взаимного непонимания», и, конечно, не случались бы казусы, подобные грубо ошибочному расчёту угловой скорости прецессии симметрического волчка в «классическом» учебном пособии, рекомендованном Министерством образования Российской Федерации для студентов физических специальностей университетов (Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. I. Механика. – 5-е изд., стереот. – М.: ФИЗМАТЛИТ, 2001, сс. 141-142).
Эйлерова постановка задачи и её критика
Итак, рассмотрим задачу о вращающемся волчке более детально, начиная с ключевого момента – с её постановки. Эйлерова постановка задачи механики о движении твёрдого тела вокруг неподвижной точки исходила из возможности описания данного движения дифференциальными уравнениями, для которых должны существовать не зависящие от времени интегралы, аналогичные вычисляемым для движения замкнутых систем. К отысканию таких интегралов движения и должно сводиться решение задачи.
Забегая вперёд, заметим, что такие интегралы движения для задачи о волчке, действительно, были найдены и именно аналитическим путём, однако лишь для некоторых форм твёрдых тел, получивших названия (по именам исследовавших их учёных) волчков Эйлера, Лагранжа и Ковалевской (в случае Гесса-Аппельрота получался вырожденный волчок Ковалевской). Для этих случаев поставленная Эйлером задача решалась с помощью аппарата эллиптических и гиперэллиптических функций, составивших основу теории интегрируемых движений твёрдого тела вокруг неподвижной точки («Интегрируемые волчки», [2]).
Каковы же основные допущения и ограничения эйлеровой постановки задачи о волчке? Прежде всего, это – безальтернативный выбор декартовой системы координат, оси которой (в случае связанной с телом и вращающейся вместе с ним системы координат) направляются по главным осям инерции тела. Если главные моменты инерции тела приняты равными постоянным величинам A, B, C, то, в выбранной системе координат, тензор инерции тела имеет диагональный вид:
- L=diag(A,B,C).
А далее следует весьма ответственный (но уже вынужденно безальтернативный) шаг: постулируется возможность векторного разложения на три составляющие по осям выбранной системы координат, во-первых, мгновенной угловой скорости вращения тела w=(p,q,r) и, во-вторых, кинетического момента тела K=(Ap, Bq, Cr).
Дифференцируя по времени каждую из составляющих кинетического момента и прибавляя к полученным результатам соответствующие проекции на оси координат векторного произведения угловой скорости и кинетического момента, Эйлер уравнивает эти суммы, принимаемые за компоненты внутреннего силового баланса, с проекциями Mx, My, Mz (на эти же оси координат) внешнего момента силы тяжести M. В результате получается векторно-тензорное уравнение, записываемое в виде системы трёх скалярных уравнений, называемых динамическими уравнениями Эйлера:
- Adp/dt + (C – B)qr = Mx; Bdq/dt + (A – C)rp = My; Cdr/dt + (B – A)pq = Mz.
В этой системе уравнений шесть неизвестных – помимо проекций мгновенной угловой скорости p, q, r на оси координат, это ещё и проекции α, β, γ вектора вертикальной оси неподвижной системы отсчёта, жёстко связанной с евклидовым пространством (в которой задан внешний момент силы тяжести M), на оси подвижной системы координат, жёстко связанной с телом. Если выразить единичный орт неподвижной системы координат через его координаты в системе, связанной с телом, то для α, β, γ получаем ещё три дифференциальных уравнения (как и выше, t – время):
- dα/dt = rβ – qγ; dβ/dt = pγ – rα; dγ/dt = qα – pβ
- называемые уравнениями Пуассона.
Заметим, что Mx=mg(z0β–y0γ), My=mg(x0γ–z0α), Mz=mg(y0α–x0β), где m – масса тела, g – ускорение свободного падения, (x0, y0, z0) – координаты смещения точки закрепления тела от его центра масс.
Совместно уравнения Эйлера-Пуассона определяют движение твёрдого тела с закреплённой точкой. Для этих уравнений известны три полных интеграла. Это интеграл энергии Ap² + Bq² + Cr² + 2mg(x0α + y0β + z0γ) = const, интеграл площадей (проекция вектора K на ось z не изменяется) Apα + Bqβ + Crγ = const, геометрический интеграл (сумма квадратов направляющих косинусов равна 1) α² + β² + γ² = 1.
Для интегрирования уравнений Эйлера-Пуассона достаточно найти ещё один первый интеграл, однако, он известен лишь в трёх специальных случаях, о которых уже говорилось выше: это волчки Эйлера, Лагранжа и Ковалевской.
Волчок Эйлера – специальный случай уравнений Эйлера-Пуассона, когда точка закрепления совпадает с центром тяжести тела. В этом случае уравнения Эйлера можно рассматривать отдельно от уравнений Пуассона (момент силы тяжести, действующей на тело, равен нулю, и кинетический момент тела неизменен). Из вида интегралов для этого случая следует, что инвариантное многообразие в трёхмерном пространстве – это пересечение эллипсоида и сферы; в то же время, составляющие кинетического момента выражаются через эллиптические функции Якоби.
Волчок Лагранжа – случай, когда два статических момента твёрдого тела равны (A = B), и координаты центра тяжести x0 = y0 = 0. Решение уравнений Эйлера-Пуассона для волчка Лагранжа выражается в эллиптических функциях.
Волчок Ковалевской – случай, когда A = B = 2C, y0 = z0 = 0, и уравнения Эйлера-Пуассона легко интегрируются, однако, для выяснения поведения решения в исходных переменных необходимо обратить преобразование Абеля. Задачу об обращении гиперэллиптических интегралов называют задачей обращения Якоби; она решается с использованием тэта-функций (Дубровин Б.А.. Нелинейные уравнения и тэта-функции. Успехи математических наук, 1981, т.36, n.2, с.11-80).
А теперь предоставим слово В.Н.Оникийчуку, раскрывшему «Великую тайну Леонарда Эйлера» (см. выше ссылку на его книгу):
“В 1880–1890-х годах французский математик Анри Пуанкаре доказал, что уравнения Эйлера-Пуассона всё-таки принципиально не интегрируются. Это означало, что никакие первые интегралы для этой задачи (кроме уже известных – Эйлера, Лагранжа и Ковалевской) в принципе не могут быть представлены какими-либо математическими формулами. За эту работу Анри Пуанкаре был награждён золотой медалью Королевской Шведской Академии наук (1889). Далее этот пессимистический вывод о принципиальной не интегрируемости уравнений Эйлера-Пуассона единодушно утверждался учёными Европы в XIX–ХХ веках. Разумеется, эту точку зрения разделяли и разделяют до сих пор российские учёные. В этом смысле данная проблема является «исчерпанной» в том смысле, что принята «окончательно» официальная точка зрения, что задача Эйлера-Пуассона принципиально не поддаётся аналитическому решению. По этой проблеме в СССР (России), а также за рубежом вышло много книг, и на эту тему защищены сотни кандидатских и докторских диссертаций. Ряд зарубежных и российских (советских) учёных за работы в этой области были удостоены высоких государственных наград. Самое невероятное в этой истории то, что эта задача полностью решается – вопреки уже всеобщей убеждённости в принципиальной невозможности решить эту задачу. Суть в том, что решения, которые предлагались за всю 250-летнюю историю этой задачи, полны противоречий, парадоксов и грубых «внутренних» нестыковок между собой. Эти обстоятельства и стали тем беспорядочным хаосом, который не дал возможности решить эту задачу до конца”.
В.Н.Оникийчук подробно разбирает историю вопроса и причины, по которым до настоящего времени задача о вращающемся волчке в постановке Эйлера не была решена. Однако проблема корректности самой постановки задачи остаётся за рамками его исследования, что оставляет открытым и вопрос о возможной альтернативе эйлеровой постановке задачи.
Понятно, что математики вправе ставить и решать (или пытаться решать) любые задачи, которые им диктует сам «материал» (количественно-пространственные соотношения, абстрагируемые из реального мира), с которым они профессионально работают. Но, если (и как только) у задачи, кроме условного обозначения или номера, появляется название с конкретным физическим содержанием, математик принимает на себя ответственность за адекватное отражение этого содержания.
В эйлеровой постановке задачи обращает на себя внимание полная симметрия динамических характеристик тела по отношению к измерениям пространства. Для твёрдого тела, начинающего своё движение с нулевых значений линейных и угловых скоростей относительно любого измерения трёхмерного физического пространства, это могло бы служить каким-то оправданием. Но ведь в названии задачи фигурирует понятие «вращающийся волчок», т.е. тело с чётко определёнными осью и плоскостью быстрого вращения. А это означает, что Эйлер в своей постановке задачи фактически проигнорировал важный качественный скачок, сопровождающий превращение движения из плоскостного в трёхмерное. Удивительно, что этот факт очень долгое время не привлекал внимания ни физиков-теоретиков, ни историков науки. Впрочем, в последнее время этот факт внимание дотошных «исследователей-любителей» (но не «официальной» науки!?) всё же привлёк.
«..."Механика Ньютона" (как, впрочем, и "классическая механика") могут быть справедливы лишь в формулировках "плоского движения", и лишь для физических тел, находящихся в плоскости движения планет Солнечной системы… И первый, и второй, и третий законы Ньютона, и закон тяготения тел – все они и получены, и справедливы только для плоского движения. Эйлер эту особенность подметил достаточно правильно, очень точно следовал Ньютону и тоже рассматривал лишь различные варианты плоского движения... Здесь нам следует заметить, что и Ньютон, и Эйлер, и Лагранж, и Эйнштейн (в отличие от Роберта Гука и Нильса Бора), в гораздо большей мере были математиками, а не физиками. И та "математизированная физика", которую мы сейчас изучаем в школе и ВУЗах, по сути является своеобразным коктейлем "результатов физических опытов" и "ошибок математических представлений" этих опытов... Уже давно следует признать, что излишняя математизация физики приводит к большому числу физических ошибок и логических парадоксов. И здесь следует лишь повторить ещё раз: физика - не математика, и никогда ею не станет… Эйлер столкнулся с достаточно серьёзной проблемой описания движения тела, которую он решить так и не смог. Проблема эта следующего содержания.Пункт 1. С одной стороны Эйлер отчётливо понимал, что рассматривать он имеет право лишь "плоское движение" тела, поскольку и Ньютон рассматривал лишь "плоское движение", и законы Кеплера сформулированы лишь для случая "плоского движения" небесных тел. Пункт 2. С другой стороны, вполне очевидно, что "плоское движение" мы имеем только в случае, когда вектор угловой скорости ортогонален вектору перемещения (или вектору скорости центра масс тела).
Пункт 3. С третьей стороны, несложно заметить, что любое "прямолинейное движение" твёрдого тела (не только "плоское движение", но и движение, которое не является "плоским") можно представить как суперпозицию прямолинейного движения центра масс и равномерного вращения этого тела вокруг его центра масс...
Проблема, с которой столкнулся Эйлер в данном случае, достаточно очевидна. В самом деле, если мы принимаем условия пунктов 1 и 2, то вынуждены отказаться от рассмотрения движений, указанных в пункте 3. Обратно, если мы принимаем условия пункта 3 то, вообще говоря, выходим за рамки удовлетворения условий пунктов 1 и 2. Эйлер нашёл весьма оригинальный (но физически не вполне верный) способ разрешения этой проблемы, который впоследствии стал традиционным для выяснения логических отношений между математикой и физикой. А именно. Эйлер не стал эту проблему "решать в лоб", а обратил внимание на тот факт, что "чисто вращательное" движение твёрдого тела всегда является плоским движением, поскольку вращение тела всегда происходит вокруг некоторой оси вращения. Следовательно, все точки тела, в этом случае, перемещаются в плоскости, перпендикулярной оси вращения. Поэтому вначале Эйлер рассмотрел только "вращательное движение тела" отдельно от "поступательного движения его центра масс". Но в этом случае, как несложно заметить, для определения "движения тела" необходимо задать не две, а три независимые координаты:
- 1.направление оси вращения, вместе с точкой центра масс тела;
- 2.величину и направление угла поворота вокруг оси вращения;
- 3.радиус-вектор интересующей нас точки тела с началом в центре масс этого тела.
Такое определение вращательного движения наиболее естественное. Казалось бы, всё просто и понятно. Задаём эти три независимые координаты, и получаем результат в виде вращательного движения. Но нет. Эйлер предпочёл эту процедуру выполнить несколько иначе... Эйлер проанализировал движение "волчка", и ввёл в рассмотрение "систему координат", отвечающую этому движению. Такой способ математического описания вращательного движения впоследствии получил название "метода Эйлера", а "система координат", отвечающая этому методу, стала называться "углами Эйлера"... "Метод Эйлера" является в настоящее время "базовым методом" описания "вращательного движения" в механике твёрдого тела (и не только в ней)... На первый взгляд здесь всё выполнено безукоризненно верно, и никаких ошибок нет. Тем не менее, именно в этом месте Эйлер допустил достаточно грубую физическую ошибку, которую с тех пор старательно переписывают все авторы из одного учебника физики в другой... Причина этой ошибки заключена в следующем... "Неподвижная система координат", связанная с центром основания прямого кругового конуса, не является в действительности "неподвижной", а является "неинерциальной системой отсчёта" (она вращается, что исключает для неё возможность быть "инерциальной"). Это в свою очередь, накладывает определённые ограничения на применение к этой системе координат "законов Ньютона" (а также законов сохранения энергии и импульса), поскольку в этой системе координат присутствуют силы инерции, которые мы должны учесть, но которые нам неизвестны, поскольку задача движения не решена. С другой стороны, если мы хотим, чтобы система координат, связанная с углами Эйлера была "инерциальной системой отсчёта" (например, движение в отсутствие действующих сил и моментов сил), то, по меньшей мере, один из углов Эйлера оказывается "избыточным". Короче говоря, если мы предполагаем, что представление Эйлера верно, то такая система координат не может быть "инерциальной". И наоборот, если система координат с углами Эйлера является "инерциальной", то хотя бы один из углов Эйлера является лишним в таком описании. Другими словами, в обоих случаях при описании движения методом Эйлера мы приходим к логическому противоречию, или "парадоксу Эйлера" описания движения твёрдого тела...
Таким образом, пытаясь преодолеть указанные выше логические проблемы в описании движения, Эйлер так и не смог решить проблему плоского движения в представлении Ньютона и Кеплера. Указанная ошибка Эйлера повлекла за собой целую серию ошибок в описании движения тела. Сюда относятся и понятие тензора инерции вращающегося тела, и разложение движения на поступательную и вращательную часть, и многие другие. Другими словами, "метод Эйлера" имеет далеко не столь общий смысл описания вращательного движения, который ему придают в современной механике».— Озолин Э.Э., 2005; [3]
Неадекватность методологии и математического аппарата
В критике "метода Эйлера" мы пойдём ещё дальше. При этом для наглядности воспользуемся занимательной игрушкой-головоломкой под названием «кубик Рубика», который удобен для наших целей тем, что все шесть его граней окрашены разным цветом. Только вращать его мы будем не «слоями», а целиком, как единое твёрдое тело.
Итак, поместим кубик в начало декартовой системы координат так, чтобы все три пары его цветных граней были перпендикулярны соответственно трём осям координат (x,y,z). Поворот кубика в пространстве будет состоять из трёх «элементарных» поворотов на 90º вокруг каждой из трёх осей координат (для определённости – против часовой стрелки).
Смысл эксперимента состоит в определении конечного результата «элементарных» поворотов кубика в зависимости от порядка их следования. Возможных вариантов (по числу перестановок «из трёх по три») всего шесть: (x,y,z), (x,z,y), (y,x,z), (y,z,x), (z,x,y), (z,y,x). А теперь всем желающим предоставляем возможность самим убедиться в том, что число различных конечных результатов трёх «элементарных» поворотов кубика тоже шесть!
Если же допустить совместные повороты не только против, но и по часовой стрелке, то к указанным шести добавятся ещё три новых результата (остальные три совпадут с уже встречавшимися среди предыдущих шести). В связи с этим возникает вопрос: если ни одному из трёх «элементарных» поворотов тела вокруг осей координат заранее не отдать предпочтения, т.е. не установить между ними строгой очерёдности, то на какой из шести (или девяти) возможных вариантов поворота следует «настраивать» уравнение движения?
Наблюдаемые в природе и технике физические процессы наложения друг на друга поворотов тел в перпендикулярных плоскостях (в отличие от их математических абстракций), спонтанно или по программе, но происходят в определённом порядке: одно из вращений оказывается первым (и основным), второе вращение, налагаясь на первое, становится нелинейно зависимым и не коммутирующим с ним, а третье вращение не коммутативно и не ассоциативно по отношению к двум предыдущим.
Выше мы рассматривали наложение конечных по величине поворотов в трёхмерном пространстве. Но аналогичная картина многозначности и неопределённости результатов наложения вращений друг на друга наблюдается и при сложении бесконечно малых величин (дифференциалов) поворотов в перпендикулярных плоскостях (что равноценно сложению угловых скоростей).
В итоге, мы должны признать, что принятый Эйлером постулат о возможности разложения вектора мгновенной угловой скорости на проекции по осям декартовой системы координат (как и обратного векторного их сложения по правилу параллелограмма или параллелепипеда) не адекватен поставленной физической задаче. На деле, эйлерова постановка задачи относится не к реальным физическим объектам (не к твёрдому телу и, тем более, не к вращающемуся волчку), а к некой математической абстракции этих объектов, представляющей интерес для «чистой математики», но не для теоретической механики (по крайней мере, не для механики макромира).
Наглядно можно убедиться в абсурдности попыток векторного сложения угловых скоростей вращений тела в трёх разных плоскостях, сопоставив величины угловых скоростей вращения вокруг своей оси, прецессии и нутации такого «большого волчка», каким является наш Земной шар.
«... Более 2000 лет назад было обнаружено явление прецессии, но объяснение его дал лишь в 1687 году Исаак Ньютон в своём бессмертном сочинении "Математические начала натуральной философии". Он правильно заключил, что вследствие суточного вращения вокруг оси Земля имеет форму слегка сплющенного у полюсов эллипсоида. Её можно рассматривать как шар с добавочной массой, расположенной вдоль экваториального пояса. Притяжение Земли Луной и Солнцем в этом случае можно разделить на две части: притяжение земного шара силой, приложенной к его центру, и притяжение экваториального пояса. Когда Луна 2 раза в месяц, а Солнце 2 раза в год отходят от плоскости земного экватора, их притяжение создаёт момент силы, стремящийся повернуть Землю так, чтобы её экватор проходил через эти светила... Быстрое вращение Земли (ведь точка её экватора перемещается со скоростью 465 м/с) создаёт гироскопический эффект, как у вращающегося волчка. Сила тяжести стремится повалить волчок, но вращение удерживает от падения, и его ось начинает движение по конусу с вершиной в точке опоры. Подобно этому, и земная ось описывает конус вокруг оси эклиптики, ежегодно отходя на 50,2" и совершая полный оборот почти за 26 000 лет. Хотя Луна имеет массу в 27 млн. раз меньше массы Солнца, но она настолько ближе к Земле, что ее действие в 2,2 раза сильнее действия Солнца. Таким образом, почти 70% прецессионного движения вызывается Луной. Луна и Солнце периодически изменяют свое положение относительно экватора. Склонение Солнца регулярно меняется в пределах ±23,5° с годичным периодом, склонение Луны меняется более сложно, в зависимости от положения узлов лунной орбиты, которые совершают один оборот по эклиптике за 18,6 года. Наклон лунной орбиты к эклиптике составляет 5° и, когда восходящий узел близок к точке весеннего равноденствия, наклон орбиты складывается с наклоном эклиптики, так что склонение Луны в течение месяца колеблется между ±28,5°. Через 9,3 года, когда к точке весеннего равноденствия подходит нисходящий узел, наклоны вычитаются, и склонение Луны меняется в пределах ±18,5°. Месячные изменения склонения Луны и годичные изменения склонения Солнца не успевают произвести значительного действия на прецессионное движение. Колебание же склонения Луны с периодом 18,6 года вызывает колебания земной оси с амплитудой 9,2", называемые нутацией. Это явление открыл английский астроном Джеймс Брадлей в 1745 году»— [4]
Ясно, что описание реальных вращений реального твёрдого тела в трёх плоскостях выходит за пределы возможностей векторно-тензорной алгебры, поскольку реальные динамические характеристики налагающихся друг на друга вращений (мгновенная угловая скорость, кинетический момент тела и др.) по осям декартовой системы координат не раскладываются и векторно не складываются. Однако никакими иными методами и средствами, для более тонкого анализа таких процессов, данный аппарат не располагает.
А существует ли вообще способ математически корректного описания и исследования таких процессов? Естественно, мы не будем принимать всерьёз предлагавшиеся известными математиками ещё в 30-е годы прошлого века, для применения в исследованиях вихревых движений, примитивные и, по большому счёту, не пригодные для решения такого рода задач методы теории вероятностей (в итоге, не оправдавшие возлагавшихся на них надежд и не давшие сколько-нибудь заметных положительных результатов).
Адекватное описание и количественно точное определение результатов наложения вращений друг на друга возможно лишь в (отвечающих реальным физическим закономерностям вращений) системах гиперкомплексных чисел, представляющих собой алгебры с делением, а, именно: некоммутативную алгебру кватернионов и неассоциативную алгебру октонионов (октав).
Заметим, что для самого Эйлера область математического знания, связанная с алгебрами с делением, отнюдь не была неведомой, Одним из свидетельств этого является оставленная им (в ряду других) «загадка» в виде широко известной кинематической формулы Эйлера, вывода которой он в своих трудах не привёл:
dx/dt = w×x
- где dx/dt – вектор линейной скорости произвольной частицы твёрдого тела,
- w – вектор угловой скорости тела,
- × – знак векторного умножения.
В терминах векторно-тензорного исчисления эта формула не выводится. А в комплексных числах, представляющих собой алгебру с векторным делением для плоскостного движения, вывод формулы трудностей не представляет. Так, если в трёхмерном физическом пространстве для произвольной точки траектории движения определена спрямляющая плоскость, образованная касательной и главной нормалью к траектории, то, принимая за начало подвижной системы координат мгновенный центр кривизны, получаем следующую взаимосвязь трёхмерной(!) координаты x (модуль которой равен радиусу кривизны траектории в данной точке) с линейной скоростью dx/dt и ускорением d²x/dt²:
- (d²x/dt²)/(dx/dt) = w ,
- (dx/dt)/w = x ,
- где w – вектор мгновенной угловой скорости.
Легко заметить, что второе выражение представляет собой не что иное, как «обращённую» (а правильнее сказать, «первородную») кинематическую формулу Эйлера, которую, в рамках ограниченных аналитических средств векторно-тензорной алгебры, автор формулы не имел возможности представить иначе, как в виде векторного произведения!
Не менее замечательна и первая из вышеприведённых формул, с которой Эйлер также был знакóм. Ведь это не что иное, как «первородная» формула для определения вращательной (вихревой) составляющей движения, которая (главным образом, трудами О.Хевисайда, «переводившего» максвелловы уравнения электродинамики с кватернионного на векторно-тензорный язык) превращена в «математического уродца» (с красивым названием, не отвечающим его реальному физическому и математическому содержанию!), а, именно, в оператор символического дифференцирования rotor («вихрь»).
Достаточно попытаться применить этот оператор к «полю скоростей» простейшего вихревого движения по винтовой линии, чтобы убедиться в его неспособности выделить вращательную (вихревую) составляющую движения, во-первых, однозначно (т.е. вне зависимости от выбранной системы координат), а, во-вторых, без побочных эффектов, не имеющих ни физического, ни математического объяснения и смысла.
Приведённые выше формулы Эйлера не только исчерпывающим образом описывают динамику плоскостной части движения, но и могут служить основой для включения в это описание второго вращения, имеющего смысл поворота плоскости (или оси) первого вращения. К сожалению (и по не объяснимым причинам), в эйлеровой постановке задачи о вращающемся волчке такая возможность осталась не реализованной. Вместо этого в динамических уравнениях Эйлера появился откровенный «ляпсус».
Действительно, главный момент инерции относительно оси быстрого вращения волчка (выше он был принят равным А), в отличие от двух других главных моментов инерции (величины В и С; обычно В=С), непосредственно входит в выражение для центробежных сил, создающих внутреннее динамическое напряжение в системе, и участвует в формировании кинетического момента, устойчивое положение которого в пространстве (при малой, по сравнению с быстрым вращением, и, к тому же, постоянной по величине скорости прецессии) представляет собой единственное препятствие для отклонения оси волчка от исходного положения (или от иного положения, занимаемого по ходу прецессии). Но из этого следует, что второй и третий главные моменты инерции (В и С), ввиду их ничтожно малого влияния на конечный результат решения задачи, в уравнения движения включаться не должны. Помимо искажения физической сути явления, это лишает уравнения движения волчка важного свойства линейности.
С другой стороны, некоммутативность второго и неассоциативность третьего вращений, отражаемые в уравнениях движения на языке алгебр с делением, отнюдь не влекут за собой неизбежную нелинейность уравнений, вопреки уже успевшему устояться в среде математиков представлению о тождественности понятий линейного и векторного пространств (последнего – в смысле и с позиций векторно-тензорной алгебры, не имеющей в своём «инструментарии» операции векторного деления).
Постановка и решение задачи в кватернионах
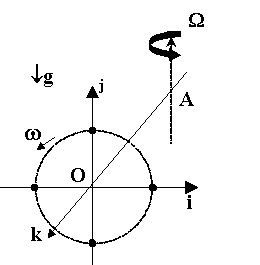
рис.1
Привяжем наши дальнейшие рассуждения и действия к конкретной модели вращающегося волчка. При этом, для начала рассмотрим предельное значение угла отклонения оси волчка (гироскопа) от вертикали, равное 90°, когда ось быстрого вращения горизонтальна (рис.1).
Принципиальную схему волчка представим в виде трёхмерной динамической системы, рабочая масса которой состоит из четырёх отдельных масс m, симметрично расположенных на расстояниях ±r от оси симметрии и начала координат О вдоль осей координат i, j и синхронно вращающихся вокруг оси k с постоянной угловой скоростью ω. Неподвижную точку А (центр прецессионного вращения) разместим на оси быстрого вращения k на расстоянии –R от начала координат.
Быстрое вращение рабочей массы в начальный момент времени происходит в плоскости (i,j). Оперирование в трёхмерном векторном пространстве (i,j,k) осуществляется по правилам кватернионного (некоммутативного) умножения:
ij=k; ji= –k; jk=i; kj= –i; ki=j; ik= –j; i²=j²=k²=ijk= –1.
Центробежные силы (для каждой из отдельных масс m равные по модулю величине mω²r) при вращении создают внутренне напряжённую динамическую структуру, реакцию которой на внешнее воздействие нам предстоит качественно и количественно оценить.
Выразим математически устойчивость вектора угловой скорости быстрого вращения волчка в пространстве. По вопросу о том, в какой системе координат и отсчёта следует описывать реакцию вращающегося твёрдого тела на внешнее воздействие, у теоретиков разногласий нет: внешнее воздействие следует рассматривать в жёстко связанной с телом (вращающейся вместе с ним) системе координат и отсчёта. Но при использовании алгебры с делением здесь появляется уточнение: при использовании такой системы координат в математической записи внешнего воздействия появляется эйлеров экспоненциальный множитель «обратного вращения» еxp(–kωt).
Далее, при кватернионном представлении второго вращения в математической записи внешнего воздействия (и в решении уравнения движения) должен появиться второй эйлеров экспоненциальный множитель, но уже с не известным заранее параметром – угловой скоростью прецессии. При этом мы сталкиваемся с достаточно громоздкими выкладками в процедуре кватернионного «умножения справа и слева» (см. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М.: «Наука», 1973, сс. 29-30).
Чтобы этого избежать, мы идём на упрощение задачи, отказываясь от представления траектории движения в целом и ограничиваясь рассмотрением движения центра масс волчка лишь в малой окрестности выбранной точки траектории.
Тогда малые смещения центра масс по дуге окружности заменяются малыми линейными перемещениями в касательной плоскости, а вращающий момент на входе динамической системы, отнесённый к величине плеча момента силы тяжести, приводится к линейному виду силового воздействия, т.е. к проекции силы тяжести, пропорциональной синусу угла наклона оси волчка к вертикали. Зная радиус прецессионного вращения, можно легко пересчитать найденное из решения уравнения движения линейное смещение центра масс волчка в величину угловой скорости прецессии.
Этим же приёмом упрощения кватернионных выкладок мы воспользуемся, когда потребуется рассмотреть прецессию волчка при произвольном угле наклона оси волчка к вертикали. Поскольку кватернионное умножение справа и слева оставляет проекции параметров движения волчка на вертикаль неизменными, то мы заранее эту часть кватернионных операций исключаем и анализируем только горизонтальную составляющую этих характеристик (так же, как это мы делаем для случая предельного значения угла наклона оси волчка, равного 90º, но только умножая плечо момента силы тяжести на синус угла отклонения оси волчка от вертикали).
Итак, необходимо математически выразить устойчивость направления оси волчка в пространстве. В неподвижной системе координат мы наблюдали бы статичную картину этого явления, которая не раскрывает существа имеющего место динамического равновесия внутренних и внешних сил (или моментов сил). Только во вращающейся системе координат представляется возможность отразить внутреннюю динамику волчка.
За основу принимаем экспериментально установленный факт безынерционности прецессии волчка: когда есть внешний вращающий момент – есть и прецессия; с прекращением внешнего воздействия прецессионное движение тут же прекращается; кроме того, при постоянном по величине внешнем воздействии скорость прецессии также постоянна.
Вышесказанное позволяет сделать вывод о том, что дифференциальное уравнение движения волчка будет иметь первый порядок. А теперь рассмотрим малое линейное отклонение центра масс волчка на величину α в касательной плоскости, перпендикулярной оси волчка, в произвольном направлении (для определённости – в направлении оси координат i на рис.1). Во вращающейся системе координат, с началом в исходной нулевой точке, в результате указанного отклонения центр масс волчка начнёт описывать окружность радиусом α вокруг начала координат, с обратным направлением вращения по отношению к внешне наблюдаемому.
То, что в неподвижной системе координат выглядит как статичная устойчивость оси волчка в пространстве, во вращающейся системе координат представляется внутренним динамическим балансом импульсов (или количества движения), удерживающих центр масс волчка на постоянной круговой орбите, что математически представляется выражением:
α еxp(kωt) = const.
Дифференцируя это выражение по времени, получаем, в отсутствие внешнего воздействия, однородное дифференциальное уравнение устойчивого динамического равновесия системы в виде баланса линейных компонентов моментов сил, приведённых к единичному моменту инерции волчка относительно оси быстрого вращения:
dα /dt + kωα = 0.
Приводя вращающий момент, создаваемый земным притяжением, к единичному моменту инерции волчка относительно оси быстрого вращения, решаем задачу о прецессии вращающегося волчка при принятых выше исходных данных:
–k(dα/dt) + ωα = –j(gR/ωr²) еxp(–kωt) (уравнение),
α = i(gRt/ωr²) еxp(–kωt) (решение).
Переводя результат решения задачи в невращающуюся систему координат (исключая из него множитель обратного вращения), убеждаемся в том, что движение представляет собой именно прецессию, т.е. медленное вращение системы в горизонтальной плоскости (на рис.1 – в положительном направлении оси i) с постоянной угловой скоростью Ω:
Ω = gR/ωr².
В случае произвольного угла наклона оси волчка к вертикали Θ, с уменьшением плеча момента силы тяжести происходит уменьшение угловой скорости прецессии пропорционально синусу указанного угла наклона:
Ω = gR sinΘ/ωr².
Если искусственно (в ограниченных условиями задачи пределах) увеличить внешний вращающий момент в вертикальной плоскости, то угловая скорость прецессии соответственно возрастёт. Ну, а если подобное внешнее воздействие будет иметь вид кратковременного импульса? Тогда, вследствие фазового сдвига на 90 градусов между направлениями внешнего силового воздействия и вызываемого им движения (с соответствующим обратным фазовым сдвигом динамической реакции системы, уравновешивающей внешнее воздействие), дополнительное движение волчка приобретёт характер незатухающего кругового движения центра масс вокруг точек траектории регулярной прецессии, как мгновенных центров ещё одного, третьего вращения, называемого нутацией.
Угловую скорость нутации W (при горизонтального расположения оси волчка) найдём, разделив ускорение свободного падения на вызываемую силой тяжести линейную скорость прецессии (для данной конструкции, или принципиальной схемы, прецессирующего волчка):
W=g/ΩR=ωr²/R², (R » r).
Особо подчеркнём, что все три вращения волчка (быстрое, прецессии и нутации) между собой динамически не связаны и механизмов взаимного обмена энергией, импульсом или моментом импульса не имеют (а ведь именно из такого ошибочного предположения исходит существующая методология анализа движения волчка, приводящая в итоге к формулам, не только не пригодным для инженерных расчётов, как, например, в «Математической энциклопедии», но и представляюшим собой откровенное издевательство над здравым смыслом и интеллектом студентов, как в «классическом» университетском учебном пособии «Механика» Ландау-Лифшица).
Заметим, что в данном случае движение центра масс происходит по поверхности равного гравитационного потенциала, без какого-либо накопления внутренней энергии или импульса системы. Тем не менее, основные признаки резонансного процесса – фазовый сдвиг на 90º выходной реакции относительно входного воздействия и линейный во времени рост результирующего углового смещения оси гироскопа – налицо.
Обратим также внимание ещё на одну важную особенность гироскопа (волчка) как интегратора входного воздействия: внешний вращающий момент –j4mgR преобразуется в линейно возрастающую во времени фазу Ωt поворота оси гироскопа. А что произойдёт при возникновении непреодолимой преграды прецессионному движению? В этом случае выходной вращающий момент в отражённом виде (со сменой знака направления воздействия на противоположный) возвращается в систему в виде нового входного воздействия –i4mgRΩt. Последнее интегрируется, при наличии свободы вертикального перемещения гироскопа, в движение вращающейся массы с угловым ускорением gR/r², означающим при R=r свободное падение с линейным ускорением g.
Этот результат решения в кватернионах задачи о волчке теоретически обосновывает наблюдаемый на опыте эффект утраты вращающейся массой гироскопических свойств при возникновении препятствия на пути прецессии. А, в более широком плане, это раскрывает «тайну», во-первых, связи силы трения и сопротивления внешней среды с первой производной, и, во-вторых, силы инерции со второй производной по времени от перемещения массы. Выясняется, в частности, физический смысл различного вида связей в веществе на молекулярном уровне. Так, в газовой, жидкой среде и в пограничных слоях твёрдых тел вращающиеся микроволчки свободно прецессируют, выполняя однократное интегрирование внешних воздействий. При этом возникают силы сопротивления, пропорциональные первой производной по времени от перемещения физического объекта. Когда же вращающимся микроволчкам становится «тесно» настолько, что они начинают препятствовать прецессии друг друга, они вынужденно превращаются в двойных интеграторов внешних воздействий. Так возникает локальный, а затем и общий для данного физического тела, эффект наличия массы со свойством инерции, отвечающим второму закону Ньютона.
Напомним, что «общепринятая» методология относит вращающийся волчок к замкнутым системам, а его прецессию – к «безатратным», т.е. с энергетической точки как бы вообще «не существующим» процессам. Однако перемещение центра масс волчка даже по поверхности равного гравитационного потенциала не может происходить «беспричинно», «беззатратно». И, естественно, при более сложной конфигурации системы возникает возможность, наряду с функцией уравновешивания внешнего воздействия, обеспечивать приток извне и накопление энергии в самóй динамической системе. В этом отношении трёхмерная гравитационно-резонансная система открывает новые и весьма широкие возможности для изобретательского и конструкторского творчества.
Есть и повод прямо сопоставить два принципиально отличающихся друг от друга подхода к проблеме вращающегося волчка (гироскопа) и достигаемых с их помощью конечных результатов: в одном случае мы имеем шесть нелинейных уравнений Эйлера-Пуассона (с шестью неизвестными), для которых не найдено общего аналитического решения (а когда и если таковое будет найдено, то ещё явственнее и очевиднее станет неадекватность, для данной задачи, применяемой методологии и математического аппарата); в другом случае мы получаем достаточно легко и просто решаемое линейное дифференциальное уравнение в кватернионах, единственным неизвестным векторным параметром которого является угловая скорость прецессии волчка.
Практические приложения задачи о волчке
История полезного применения необычного свойства волчка сохранять положение оси вращения в пространстве насчитывает уже более столетия.
«Слово "гироскоп", придуманное Леоном Фуко (1819-1868), состоит из двух греческих слов: "гирос" - вращение и "скопео" - наблюдать, смотреть. Итак, гироскоп - это "наблюдатель вращения". Сейчас гироскопы "наблюдают" вращение самых разнообразных объектов - кораблей, самолетов, ракет, спутников и многих других. Л.Фуко, создавая свой лабораторный прибор (гироскоп), хотел с его помощью наблюдать вращение Земли относительно абсолютного пространства... В качестве тела, предназначенного для быстрого вращения, Л.Фуко выбрал маховик, который был установлен в кардановом подвесе, названным так по имени Джероламо Кардано (1501-1576) - итальянского философа, врача, математика и техника (но приписываемый его авторству карданов подвес ещё в XIII веке был описан французским архитектором Уйларсом де Гонкуром).Уже первые опыты обнаружили ещё одно интересное свойство гироскопа - практическую безинерционность прецессионного движения маховика. Если к маховику мгновенно приложить и снять момент внешних сил (например, слегка ударить молоточком но внутреннему кольцу карданова подвеса), то также практически мгновенно возникнут и исчезнут угловая скорость прецессии и гироскопический момент... В результате внутреннее кольцо не повернётся вокруг своей оси. Всякое другое материальное тело в подобной ситуации продолжало бы двигаться по инерции, отклоняясь всё дальше от начального положения. У маховика гироскопа движение по инерции также есть, но оно. выражается не в одностороннем отклонении от начального положения, а в мелком, быстро затухающем дрожании около этого положения. Мелкое, быстро затухающее дрожание маховика называется нутацией, что в переводе с латинского языка означает "колебание".
В своих докладах Парижской академии наук Л.Фуко указал также на то, что маховик его прибора, лишённый одной степени свободы, должен стремиться совместить ось своего вращения с вектором абсолютной переносной скорости вращения основания. Теперь этот результат легко можно получить с помощью правила Н.Е.Жуковского, во времена же Л.Фуко это было неожиданным открытием. Впечатление ещё более усилилось, когда Л.Фуко пояснил, что с помощью гироскопа, имеющего только дне степени свободы, можно определять направление на Северный полюс Земли и широту места установки прибора... Лишив трёхстепенной гироскоп одной степени свободы, Л.Фуко открыл замечательное свойство двухстепенного гироскопа. Итак, в своих работах Л.Фуко указал на принципиальную возможность создания гироскопических приборов трёх различных назначений: свободного гироскопа, способного хранить неизменной ориентацию оси маховика в абсолютном пространстве, гироскопического компаса, гироскопического измерителя широты...
В 1886 году французский адмирал Флерие предложил новый прибор - секстан - для измерения географической широты местоположения корабля во время шторма, основой которого являлся быстро вращающийся волчок. Во время работы прибор удерживали за рукоятку в вертикальном положении. С помощью ручного насоса вовнутрь его через шланг накачивали сжатый воздух, который ударял направленными струями в боковую поверхность волчка и приводил его во вращение. При весе волчка в 175 г удавалось сообщить ему вращение со скоростью около 3000 об/мин. Для обеспечения вращения волчка неизменно в горизонтальной плоскости его центр тяжести располагали примерно на 1 мм ниже точки опоры. Приведённый во вращение волчок даже при отклонениях рукоятки от вертикального положения продолжал оставаться в горизонтальной плоскости, обеспечивая на качающемся корабле искусственный горизонт...
Без сомнения, установившиеся методы проектирования и технологические приёмы изготовления гироскопических компасов были в полной мере использованы самолётостроителями, что и оказало решающее влияние на сравнительно быстрое внедрение гироскопических приборов в авиацию. Так, уже в первую мировую войну русские военные самолёты были оборудованы гироскопическими указателями горизонта. Русская авиация не только не отставала от зарубежных стран в деле использования гироскопических приборов на самолёте, но часто являлась пионером их внедрения. Так, например, в 1917 г. русские лётчики А.Н.Журавченко и Г.Н.Алехнович совершили на самолёте "Илья Муромец" слепой полёт, выдерживая прямолинейный курс в заданном направлении по гироскопическому указателю поворотов...
Работы советских учёных А.Н.Крылова, Б.В.Булгакова, С.С.Тихменева, Г.В.Коренева, А.Р.Бонина, Г.О.Фридлендера и многих других в содружестве с выдающимися конструкторами Е.Ф.Антиповым, Е.В.Ольманом, Р.Г.Чичикяном, А.И.Марковым и другими талантливыми инженерами обеспечили оснащение советской авиации высококачественными гироскопическими приборами.
В двадцатых годах текущего столетия в дополнение к указателю поворотов создаются авиационные гироскопические указатели курса и горизонта, которые стали в настоящее время обязательными навигационными приборами самолёта любого типа. В начале тридцатых годов советские конструкторы Д.А.Браславский, М.М.Качкачян и М.Г.Эйлькинд первыми в мире разработали, построили и испытали гиромагнитный компас, получивший в настоящее время широкое распространение в авиации всех стран мира. Гироскопические приборы позволяют измерять углы, угловые скорости и ускорения при отклонении самолёта от заданного направления. Пользуясь гироскопическими приборами, определяют линейные скорости и ускорения движения самолёта. Наконец, они облегчают физический труд лётчика, управляя полётом самолета автоматически»— [5]
Казалось бы, резервы расширения областей применения гироскопических свойств волчка близки к исчерпанию. Однако постановка и решение задачи о волчках в кватернионах даёт развитию и практическому применению их необычных свойств принципиально новое направление. Оно вытекает из более глубокого уяснения физической сути гироскопического эффекта.
Гироскопический эффект оказывается возможным в силу того, что быстрое вращение создаёт внутренне напряжённую динамическую структуру, на которой внешнее силовое воздействие «размывается» по плоскости вращения так, что в любой момент времени оно не достаточно для мгновенного приведения массы во второе вращение. Только суммарное воздействие (проинтегрированное аналогично соответствующей математической процедуре и, при этом, с фазовым сдвигом на 90 градусов, поскольку процесс идёт по кругу) реализуется в наблюдаемое явление прецессии.
Волчок, подвешенный за один конец своей оси в гравитационном поле, никакой потенциальной энергией не обладает. Половина веса волчка «уничтожается» реакцией неподвижной опоры: сила тяжести есть, но в этой точке интеграл по пути движения (из-за полного отсутствия самого движения) тождественно равен нулю. Вторая половина веса волчка, давившая на вторую опору, после устранения опоры трансформируется во вращающий момент, перемещающий второй конец оси (а, значит, и центр тяжести всего волчка) по горизонтали, вдоль которой потенциал поля не изменяется, а, значит, и здесь никакой потенциальной энергии не затрачивается.
Но ведь перемещение центра тяжести волчка в пространстве всё-таки происходит, значит, реально ощутимое воздействие совершается, причём, именно силой гравитации (других сил здесь нет). Это происходит благодаря способности динамической системы трансформировать (сдвигать на 90 градусов по фазе вращения и, следовательно, в пространстве) вертикальный, статический баланс сил (тяжести и реакции опоры) в горизонтальный, динамический баланс моментов сил, где роли чётко разделены: момент силы тяжести осуществляет поворот оси волчка в горизонтальной плоскости, а ответная реакция волчка в виде силы инерции, трансформируясь из горизонтальной плоскости обратно в вертикальную (т.е. сдвигаясь по фазе ещё раз на 90 градусов), уравновешивает (уже не статически, как опора, а динамически, за счёт движения) оставшуюся без опоры половину веса волчка.
Никаких «фантазий» для объяснения этого процесса не требуется: всё чётко видно из решения дифференциального уравнения (но только составленного не в терминах векторно-тензорного исчисления, а в кватернионах или, в упрощённом виде, в комплексных числах). При этом, новые важные перспективы открывает не спонтанное (как в природе, вынужденной по необходимости переходить на двойное интегрирование внешних силовых воздействий по второму закону Ньютона), а планомерное повышение порядка дифференциального уравнения движения тела, вращающегося и одновременно колеблющегося в резонанс с частотой вращения. Это открывает возможность для создания гравитационного двигателя, выполняющего (полезную) работу без снижения гравитационного потенциала рабочей массы.
Диссипативные силы, тормозящие вращение волчка, конечно, нельзя сбрасывать со счетов, и «подкрутка» волчка время от времени необходима, но эти энергетические потери никакого отношения к существу проблемы извлечения гравитационной энергии без снижения потенциала рабочей массы не имеют. Извлекаемой энергии, при достаточной добротности резонансных систем, в которых задействованы рабочие массы, хватит не только на покрытие естественных диссипативных потерь, но и на совершение полезной работы.
В итоге, проблема создания «гравитационных perpetuum mobile» оказывается сугубо технической или технологической: как только внутренние потери динамической системы снизятся до приемлемого уровня добротности гравитационно-резонансных систем, так станет не только необходимым, но и целесообразным практическое освоение неисчерпаемого, вездесущего и экологически безупречного источника гравитационной энергии.
Величине доступной для извлечения гравитационной энергии можно дать и количественную оценку. Умножая уравнение баланса сил на скорость движения гравитационно-резонансной системы и учитывая, что максимальное значение полезной мощности достигается при равенстве внутренней (затратной) и внешней (полезной) нагрузок, а также снижая ещё вдвое полезную мощность с учётом «балластных» свойств маховика, выполняющего функцию стабилизации вращения, получаем теоретический предел полезной мощности гравитационно-резонансных двигателей данного типа для работы в наземных условиях при величине суммарной рабочей массы m:
- Р max = mg²/4b
- где b – суммарный (включая влияние полезной нагрузки) удвоенный коэффициент затухания гравитационно-резонансной системы.
Естественно, с помощью такого рода гравитационно-резонансных «вечных двигателей» может решаться и «обратная задача» преобразования накопленной энергии в поступательное движение транспортных средств и даже летательных (включая космические) аппаратов. Но здесь, прежде всего, хотелось бы с более общих позиций посмотреть на «энергетический аспект» проблемы. Со школьной скамьи, через университетские аудитории, научные кафедры, исследовательские лаборатории и рабочие кабинеты экспертов, – всюду нас сопровождает замечательная математическая формула теоретической физики, выведенная для энергии E, которой обладает масса m в поле земного тяготения с ускорением свободного падения g на высоте h над поверхностью Земли:
- E= mgh
Из этой формулы следует, что гравитационная энергия как физическая реальность возникает только при взаимодействии трёх указанных в ней компонентов: в частности, если нет перепада высот между начальной и конечной точками движения массы, или траектория движения представляет собой замкнутую кривую, то никакой энергии из такого движения извлечь невозможно.
И у физиков-теоретиков при этом не возникает никаких предположений на тот счёт, где же находят свои «перепады высот», для поддержания энергии собственного движения во Вселенной, её бесчисленные и вечные обитатели, включая имеющих, по человеческим меркам, бесконечно большие и бесконечно малые размеры. Ведь если эти объекты обнаруживают себя (для нас – визуально или инструментально), то они часть своей энергии теряют и должны каким-то образом пополнять. А источников пополнения энергии не видно! Но суть дела в том, что приведённая выше формула в общем случае неверна, и физические объекты могут черпать гравитационную энергию для поддержания собственного движения (включая и жизнедеятельность высокоорганизованных форм материи) без использования перепадов высот в гравитационных полях.
Для осуществления такого процесса, помимо наличия массы и гравитационной силы, необходимо лишь вращение и, в соответствии с динамическими параметрами последнего, – совпадение частот вращения и собственных колебаний массы, т.е. то, что мы и называем резонансом (в данном случае – гравитационным).
В природе резонансные процессы инициируются и развиваются путём «естественного отбора». Но человек способен моделировать и реализовывать их на научной основе (теоретическую физику, в её нынешнем «застойном» состоянии, просим здесь в виду не иметь!). Гравитационные силы как таковые – неиссякаемый источник энергии, а «трансформатором», способным извлекать эту, недоступную обычным техническим средствам, т.е. «глубоко законсервированную», энергию, выступают динамические системы с достаточно сложным внутренним движением (вращением и резонансными колебаниями на частоте вращения).
Ещё одна перспективная область практического применения «гравитационно-резонансных волчков» – «безопорное» движение. Кавычки в слове «безопорное» на законных основаниях можно снять: динамическая система, действительно, не нуждается во внешней опоре, создавая собственную внутреннюю опору в плоскости, перпендикулярной внешней гравитационной силе. Если движение системы совпадает по направлению с гравитационной силой, то это позволяет (частично или полностью) сэкономить энергию за счёт внешней силы. В противном случае потребуется дополнительная энергия для её преодоления. А это, в свою очередь, ставит в повестку дня вопрос создания ёмких и компактных «энергетических капсул», в которых энергия будет заблаговременно накапливаться для последующего целенаправленного использования.
Подводя общий итог, заметим, что теоретическая физика (и, прежде всего, теоретическая механика) в настоящее время не заканчивает, а только начинает своё действительное развитие!
Литература
- 1. Leonardi Euleri. Opera omnia. Series secunda. Opera mechanica et astronomica. Theoria motus corporum solidorum seu rigorum (Volumes prius). Edidit Charles Blanc, Bernae. MCMXLVIII.
- 2. Гамильтон У.Р. Избранные Труды. Оптика. Динамика. Кватернионы. – М.: Наука, 1994.
- 3. Оникийчук В.Н. Великая тайна Леонарда Эйлера. – СПб.: НПО «Профессионал», 2007.
- 4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. I. Механика. – 5-е изд., стереот. – М.: ФИЗМАТЛИТ, 2001.
- 5. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М.: «Наука», 1973.
- 6. Петров А.М. Реактивная динамика открытых систем (резонанс, вихреобразование, гироскопия, электромагнетизм). – М.: Издательство «Спутник +», 2010. – 52 с.
Ссылки
- http://www.mirrabot.com/work/work_21119.html
- «Интегрируемые волчки», http://ok.on.ufanet.ru/zoo/tops.htm
- Дубровин Б.А.. Нелинейные уравнения и тэта-функции. Успехи математических наук, 1981, т.36, n.2, с.11-80.
- Озолин Э.Э. http://ozes-world.narod.ru/PhMetaPh/3_10/PhMPh3_10.htm
- http://www.diada.ru/forum/index.php?showtopic=268&st=0
- http://www.pereplet.ru/obrazovanie/stsoros/634.html