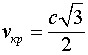Гравитационный дефект масс
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: |
|
| Учёная степень: | |
| Сайт: | |
Рассмотрим одно явление, которое имеет прямое отношение к случаю высвобождения больших величин энергии. Возьмем случай, когда пробное тело с массой 
падает на очень массивное тело с массой 
, радиус которого равен 
(в дальнейшем тело и тело ). Предположим, что в начальный момент времени расстояние между телами очень велико и что выполняется соотношение >>. Буде также считать, что плотность массивного тела 
. Скорость падения тела на поверхность тела при этом может быть найдена из соотношения:
(1)
где 
- гравитационная постоянная. Если перейти к плотности вещества массивного тела, то соотношение (1) можно переписать следующим образом:
(2)
Очевидно, что кинетическую энергию, которой обладает падающее тело, оно получила от гравитационного поля тела . Эта кинетическая энергия падающего тела при его падении на поверхность массивного тела превратиться в тепловую энергию и будет излучена в окружающее пространство в виде электромагнитных волн.
Из сказанного можно заключить, что конечная суммарная масса двух тел не будет равна сумме масс тел до начала падения:
т.е. существует гравитационный дефект масс. Соотношение меду 
и 
можно найти, зная ту кинетическую энергию, которой обладало тело при падении на тело . Эту энергию можно вычислить из соотношения
При записи этого выражения учтено то обстоятельство, что при падении тела в гравитационном поле ускорение этого тела не зависит от его массы. Поэтому соотношения (1) и (2) верны даже для релятивистских скоростей. Теперь нетрудно вычислить гравитационный дефект масс.
(3)
При падении на земную поверхность этот эффект составляет ~ 
.
Из соотношения (3) видно, что прибавка 
может быть как меньше, так и больше, чем . Если < , то при падении тела суммарная масса увеличивается. Если же = , то рост суммарной массы прекращается, и все масса падающего тела превращается в тепловое излучение. При этом массивное тело превращается в идеальную наковальню, превращающую всю массу падающего тела в энергию электромагнитного излучения.
Как легко видеть из соотношения (3), скорость падения (назовем эту скорость критической) тела на поверхность тела определится соотношением
(4)
т.е. значительно меньше скорости света.
Если известна плотность массивного тела, то, используя соотношения (2) и (4), нетрудно найти критический радиус этого тела:
Под этим понятием будем понимать то значение радиуса, при достижении которого дальнейший рост массы тела становится невозможным.
Может ли иметь место рассмотренная ситуация для космических объектов, например для нейтронных звезд. Известно, что нейтронные звезды (пульсары), имеют очень высокую плотность [1]. Так пульсар с массой ~
кг (масса Солнца) имел бы радиус всего около 10 км. Его плотность при этом составила бы ~
кг/м3. При такой плотности критический радиус составлял бы около 15 км., а масса составила бы ~ 3.4 масс Солнца. Это означает, что при достижении таких размеров и такой массы нейтронная звезда больше не может увеличивать ни своих размеров, ни свою массу, т.к. любые падающие на неё объекты будут полностью превращаться в энергию.
По предварительным подсчетам в нашей галактике насчитывается около 300 тысяч нейтронных звезд [1]. Что случиться, если нейтронная звезда столкнется с такой же нейтронной звездой как она сама? Очевидно, что произойдет полная аннигиляция нейтронного вещества и превращение его в энергию. Беря нейтронную звезду с критическим радиусом 15 км. и массой ~ 3.4 масс Солнца, получаем величину энергии 
Дж. Это значение энергии очень близко к той энергии, которая характеризует взрыв в ядре галактики NGC 3034. Во время этого взрыва из ядра галактики было выброшено громадное количество материи по своей массе равное 
масс Солнца. Это явления не находит пока своего объяснения, т. к. не известны те источники энергии, которые могут привести к столь грандиозному взрыву. Рассмотренный процесс столкновения нейтронных звезд и может являться именно таким источником.
По своей сути такой взрыв – это взрыв ядерного заряда очень большой мощности. Выделение столь значительных количеств энергии будет сопровождаться разогревом и превращением в плазму больших количеств окружающей материи. Это в свою очередь приведет к возникновению таких же электрических полей, как и при взрыве ядерной бомбы, только гораздо более значительных. Наличие таких полей в окружающем пространстве должны приводить к возникновению специфических поляризационных эффектов. К ним можно отнести поляризацию в электрических полях атомов и молекул и возникновение электрических диполей, что будет приводить к поляризации электромагнитных волн распространяющихся в плазме.
Литература
- 1. Агекян Т. А. Звёзды, галактики, метагалактика. Изд. Наука, 1981. – 415 с.
