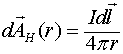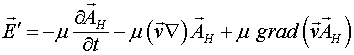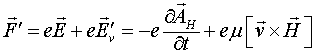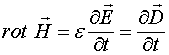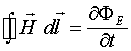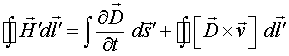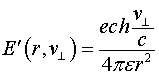Главная ошибка современной электродинамики
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: | |
Содержание
Введение
Современная классическая электродинамика построена на основе экспериментальных данных по наблюдению электрических процессов, имеющих место в материальных средах и в вакууме и состоит из двух, не связанных между собой разделов. С одной стороны это уравнения Максвелла, которые описывают волновые процессы в материальных средах. Но эти уравнения не описывают силового взаимодействия неподвижных зарядов и токонесущих систем. Поэтому приходится вводить экспериментальный постулат о силе Лоренца.
Однако при такой постановке вопроса возникает проблема, которая в классической электродинамике не решена до настоящего времени. Магнитное поле в данном случае выступает в роли некоторой самостоятельной субстанции, с которой происходит силовое взаимодействие заряда. Но в случае силового взаимодействия токонесущих систем, магнитное поле, с которым взаимодействует движущийся заряд, в свою очередь создаётся сторонними проводниками, по которым протекают токи. Поэтому в конечном итоге в соответствии с третьим законом Ньютона, силы действующие на движущийся заряд, приложены к этим токонесущим проводникам. Но в современной электродинамике нет ответа, каким образом происходит это взаимодействие и куда и как приложены ответные силы реакции.
Существенным недостатком современной классической электродинамики является и то, что в ней отсутствуют законы преобразования полей при переходе из одной инерциальной системы (ИСО) в другую. Этот недостаток восполняет специальная теория относительности (СТО), которая предполагает, что фазовая скорость электромагнитных волн одинакова во всех инерциальных системах. Но этот постулат приводит к неприемлемым с точки зрения физики выводам. Например, из СТО следует, что при стремлении скорости тела к скорости света, его размеры, параллельные скорости, стремятся к нулю. Для такого сжатия нужна колоссальная энергия, но откуда такая энергия берётся, в СТО ответа нет.
Все указанные проблемы решаются путём введения в классической электродинамике, скалярного потенциала заряда, зависящего от скорости его относительного движения. Этот закон является основополагающим законом, и из него следуют все остальные законы электродинамики. Однако этот важный факт до настоящего никем замечен не был, что и является главной ошибкой современной электродинамики.
Законы магнитоэлектрической и электромагнитной индукции
Современная классическая электродинамика построена на основе экспериментальных данных по наблюдению электрических процессов, имеющих место в материальных средах и в вакууме и состоит из двух, не связанных между собой разделов. С одной стороны это уравнения Максвелла, которые описывают волновые процессы в материальных средах. Но эти уравнения не описывают силового взаимодействия неподвижных зарядов и токонесущих систем. Поэтому приходится вводить экспериментальный постулат о силе Лоренца
(1.1)
где ![]() - скорость заряда двигающегося в магнитном поле.
- скорость заряда двигающегося в магнитном поле.
Однако при такой постановке вопроса возникает проблема, которая в классической электродинамике не решена до настоящего времени. Магнитное поле в данном случае выступает в роли некоторой самостоятельной субстанции, с которой происходит силовое взаимодействие заряда. Но в случае силового взаимодействия токонесущих систем, магнитное поле, с которым взаимодействует движущийся заряд, в свою очередь создаётся сторонними проводниками, по которым протекают токи. Поэтому в конечном итоге в соответствии с третьим законом Ньютона, силы действующие на движущийся заряд, приложены к этим токонесущим проводникам. Но в современной электродинамике нет ответа, каким образом происходит это взаимодействие и куда и как приложены ответные силы реакции.
Существенным недостатком современной классической электродинамики является и то, что в ней отсутствуют законы преобразования полей при переходе из одной инерциальной системы (ИСО) в другую. Этот недостаток восполняет специальная теория относительности (СТО), которая предполагает, что фазовая скорость электромагнитных волн одинакова во всех инерциальных системах. Но этот постулат приводит к неприемлемым с точки зрения физики выводам. Например, из СТО следует, что при стремлении скорости тела к скорости света, его размеры, параллельные скорости, стремятся к нулю. Для такого сжатия нужна колоссальная энергия, но откуда такая энергия берётся, в СТО ответа нет.
Основная задача законов электродинамики заключается в выяснении причин появления в пространстве электрических полей, а, следовательно, и сил действующих на заряд, в данной точке пространства, в данной ИСО. Такие поля могут возникать при изменении расположения других зарядов вокруг заданной точки пространства. Если вокруг рассматриваемой точки имеется какая-то статическая конфигурация зарядов, то напряженность электрического поля в этой точке будет определяться соотношением ![]() , где
, где ![]() скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций.
скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций.
Записывая соотношение (1.1) молчаливо предполагается, что скалярный потенциал в точке наблюдения не зависит от скорости этой точки и если эта точка движется вдоль эквипотенциальной поверхности, то потенциал не меняется. Если изменить расположение зарядов, то этой новой конфигурации будут соответствовать и другие значения скалярного потенциала, а, следовательно, и другие значения напряженности электрического поля. Но такое перемещение зарядов в пространстве в обязательном порядке сопряжено с их ускорением и последующим замедлением. Ускорение или замедление зарядов также может приводить к возникновению в окружающем пространстве электрических полей индукции.
Основным законом индукции в классической электродинамике является закон Фарадея, который записывается следующим образом:
(1.2)
где ![]() - вектор магнитной индукции,
- вектор магнитной индукции, ![]() - поток магнитной индукции, а
- поток магнитной индукции, а ![]() - магнитная проницаемость среды.
- магнитная проницаемость среды.
Из этого закона следует, что циркуляция вектора электрического поля равна изменению потока магнитной индукции через площадку, которую охватывает данный контур. Сразу подчеркнём то обстоятельство, что рассматриваемый закон представляет процессы взаимной индукции, т.к. для получения циркуляции вектора ![]() берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.2) получают первое уравнение Максвелла
берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.2) получают первое уравнение Максвелла
(1.3)
Сразу укажем на терминологическую ошибку. Закон Фарадея следует называть не законом электромагнитной индукции, как это делается сейчас в существующей литературе, а законом магнитоэлектрической индукции, т.к. изменение магнитных полей приводит к возникновению электрических полей, а не наоборот. На эту терминологическую ошибку впервые обратил внимание автор работ.
Но здесь необходимо сделать одно замечание. Переход от интегральной формы (1.2) к дифференциальной форме (1.3) не вполне законен. Правомерность такого перехода справедлива только в том случае, когда контур интегрирования в левой части соотношения (1.3) охватывает площадь интегрирования в интеграле правой части. Но опыты, которые провел Фарадей, совсем не предполагают этого, контур интегрирования в левой части, а вернее проволока, в которой индуцировалась э.д.с., может не совпадать с границами площадки интегрирования в правой части. Главным условием соблюдения соотношения (1.2) являлось то, что контур интегрирования в правой части должен охватывать контур интегрирования в левой. Примером тому может служить случай длинного соленоида, когда поток индукции сосредоточен во внутренней его части, а контур интегрирования может проходить за его пределами, где магнитных полей нет. Важно только, чтобы контур интегрирования в левой части соотношения (1.2) охватывал соленоид.
Введём векторный потенциал ![]() , удовлетворяющий равенству
, удовлетворяющий равенству ![]() , где контур интегрирования совпадает с контуром интегрирования в соотношении (1.2), а вектор
, где контур интегрирования совпадает с контуром интегрирования в соотношении (1.2), а вектор ![]() определен на всех его участках, тогда
определен на всех его участках, тогда
(1.4)
Путём введения вектор ![]() обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора
обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора ![]() по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор
по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор ![]() , связан с магнитным полем соотношением:
, связан с магнитным полем соотношением:
(1.5)
Таким образом, вектор ![]() является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
Если имеется прямой проводник с током, то вокруг него образуется поле векторного потенциала, в этом случае ![]() и, следовательно, в окрестностях такого проводника возникает также и магнитное поле, которое изменяется при изменении тока в проводнике. Отрезок провода длиной
и, следовательно, в окрестностях такого проводника возникает также и магнитное поле, которое изменяется при изменении тока в проводнике. Отрезок провода длиной ![]() , по которому протекает ток
, по которому протекает ток ![]() , генерирует в дальней зоне (имеется в виду, что расстояние
, генерирует в дальней зоне (имеется в виду, что расстояние ![]() значительно больше длины отрезка) векторный потенциал
значительно больше длины отрезка) векторный потенциал
Это соотношение может быть переписано и по-другому:
где ![]() - заряд, приходящийся на единицу длины проводника, по которому протекает ток.
- заряд, приходящийся на единицу длины проводника, по которому протекает ток.
Отметим то обстоятельство, что векторный потенциал убывает, как ![]() , и по этому же закону, в соответствии с соотношением (1.4), убывают и индуцируемые электрические поля. Магнитные же поля, поскольку
, и по этому же закону, в соответствии с соотношением (1.4), убывают и индуцируемые электрические поля. Магнитные же поля, поскольку ![]() , убывают, как
, убывают, как ![]() , и при больших расстояниях ими можно пренебречь. Таким образом, на больших расстояниях закон индукции продолжает работать, однако, индуцируемые электрические поля уже полностью зависят только от векторного потенциала и очень важно то, что убывают они уже не по закону
, и при больших расстояниях ими можно пренебречь. Таким образом, на больших расстояниях закон индукции продолжает работать, однако, индуцируемые электрические поля уже полностью зависят только от векторного потенциала и очень важно то, что убывают они уже не по закону ![]() , как в случае скалярного потенциала, а как
, как в случае скалярного потенциала, а как ![]() , что характерно для излучающих систем.
, что характерно для излучающих систем.
До сих пор решение вопроса о возникновении электрических полей в движущихся системах можно было осуществлять двумя путями. Первый - заключался в вычислении силы Лоренца, действующей на движущиеся заряды, второй путь заключался в измерении изменения магнитного потока через исследуемый контур. Оба метода давали одинаковый результат. В связи с непониманием физической природы такого положения дел и начали считать, что униполярный генератор является исключением из правила потока [1].
Рассмотрим эту ситуацию подробнее.
Для того чтобы ответить на поставленный вопрос, следует несколько изменить соотношение (1.4), заменив в нём частную производную на полную:
(1.6)
Штрих около вектора ![]() означает, что это поле определяется в движущейся системе координат, в то время как вектор
означает, что это поле определяется в движущейся системе координат, в то время как вектор ![]() определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.6) можно переписать следующим образом:
определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.6) можно переписать следующим образом:
где ![]() - скорость штрихованной системы.
- скорость штрихованной системы.
Следовательно, дополнительная сила, действующая на заряд в движущейся системе, запишется
Эта сила зависит только от пространственных производных векторного потенциала и скорости штрихованной системы.
Заряд, движущийся в поле векторного потенциала ![]() со скоростью
со скоростью ![]() , обладает также потенциальной энергией [1]
, обладает также потенциальной энергией [1]
Поэтому должна существовать еще одна сила, действующая на заряд в движущейся ИСО, а именно:
Таким образом, величина ![]() играет такую же роль, что и скалярный потенциал
играет такую же роль, что и скалярный потенциал ![]() , градиент которого дает электрическое поле.
, градиент которого дает электрическое поле.
Следовательно, суммарная сила, которая действует на заряд, движущийся в поле векторного потенциала, может иметь три составляющие и запишется как
(1.7)
Первая из составляющих этой силы действует на неподвижный заряд, когда векторный потенциал имеет локальную производную по времени. Вторая составляющая также определяет изменения векторного потенциала во времени, но они связаны уже с движением заряда в пространственно меняющемся поле этого потенциала. Совсем иная природа у силы, которая определяется последним слагаемым соотношения (1.7). Она связана с тем, что заряд, двигающийся в поле векторного потенциала, обладает потенциальной энергией, градиент которой и дает силу. Из соотношения (7) следует
(1.8)
Это и есть полный закон взаимной индукции. Он определяет все электрические поля, которые могут возникать в заданной точке пространства, причем эта точка может быть как неподвижной, так и движущейся. Этот единый закон включает в себя и закон Фарадея, и ту часть силы Лоренца, которая связана с движением заряда в магнитном поле. Этот закон без всяких исключений дает ответ на все вопросы, касающиеся взаимной магнитоэлектрической индукции. Показательно, что, если взять ротор от обеих частей равенства (1.8), пытаясь получить первое уравнение Максвелла, то сразу будет потеряна существенная часть информации, т.к. ротор от градиента тождественно равен нулю.
Если выделить те силы, которые связаны с движением заряда в поле векторного потенциала, и учесть, что
то из (1.7) получим
(1.9)
Учитывая (1.5), запишем:
(1.10)
или
(1.11)
Окончательно:
(1.12)
Может показаться, что соотношение (1.12) представляет силу Лоренца, однако, это не так. В этом соотношении и поле ![]() , и поле
, и поле ![]() являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.12) добавить слагаемое
являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.12) добавить слагаемое ![]() :
:
где ![]() - скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
Теперь соотношение (1.8) можно переписать следующим образом:
- скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
Теперь соотношение (1.8) можно переписать следующим образом:
(1.13)
или, собрав первые два члена в полную производную векторного потенциала по времени, и, внеся под знак градиента два последних члена правой части соотношения (1.13), получим:
(1.14)
Если обе части соотношения (14) умножить на величину заряда, то можно получить полную силу, действующую на заряд. От силы Лоренца (1.1) она будет отличаться силой  . Из соотношения (1.14) видно, что величина
. Из соотношения (1.14) видно, что величина ![]() играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (1.14) и учесть, что
играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (1.14) и учесть, что ![]() , то получим:
, то получим:
Если в данном соотношении заменить полную производную на частную, т.е. считать, что поля определяются только в заданной инерциальной системе, то получим первое уравнение Максвелла.
Ранее сила Лоренца рассматривалась как фундаментальный опытный факт, не связанный с законом индукции. Расчетным путем получить последнее слагаемое правой части соотношения (1.12) можно было только в рамках СТО. В данном случае все слагаемые соотношение (1.12) получены из закона индукции в рамках преобразований Галилея. Причем соотношение (1.12) это и есть полный закон взаимной индукции, если его записать в терминах векторного потенциала (1.14). Это есть как раз то правило, которое дает возможность, зная поля в одной ИСО, вычислять поля в другой инерциальной системе, и этого правила до сих пор не было в классической электродинамике.
Теперь и уравнения Максвелла можно записать в терминах ![]() и
и ![]()
(1.15)
где ![]() - суммарная плотность тока для заданной среды, являющаяся функцией векторного потенциала.
- суммарная плотность тока для заданной среды, являющаяся функцией векторного потенциала.
Закон Фарадея показывает, каким образом изменение магнитных полей приводит к появлению электрических полей. Однако возникает вопрос о том, приводит ли изменение электрических полей к возникновению каких-либо других полей и, в частности, магнитных? Ответ на этот вопрос дал Максвелл, введя ток смещения в свое второе уравнение. В случае отсутствия токов проводимости второе уравнение Максвелла выглядит следующим образом:
где ![]() - электрическая индукция.
От этого соотношения нетрудно перейти к выражению
- электрическая индукция.
От этого соотношения нетрудно перейти к выражению
(1.16)
где ![]() поток электрической индукции.
поток электрической индукции.
Однако для полного описания процессов взаимной электрической индукции соотношения (1.16) недостаточно. Как и в случае закона Фарадея, следует учесть то обстоятельство, что поток электрической индукции может меняться не только за счет локальной производной электрического поля по времени, но и за счет того, что контур, вдоль которого производится интегрирование, может двигаться в пространственно меняющемся электрическом поле. Это означает, что в соотношении (1.16), как и в случае закона Фарадея, следует заменить частную производную на полную. Обозначая штрихами поля и элементы контура в движущейся ИСО, получим:
и далее
(1.17)
Для электронейтральной среды ![]() , поэтому последний член правой части в этом выражении будет отсутствовать. Для этого случая соотношение (1.17) будет иметь вид:
, поэтому последний член правой части в этом выражении будет отсутствовать. Для этого случая соотношение (1.17) будет иметь вид:
(1.18)
Если в этом соотношении перейти от интегрирования по контуру к интегрированию по поверхности, то получим:
(1.19)
Если, исходя из этого соотношения, записать поля в данной инерциальной системе, то штрих около ![]() и второй член правой части исчезнут, и получим ток смещения, введенный Максвеллом. Но Максвелл ввел этот параметр, не прибегая к закону электромагнитной индукции (1.17). Если свой закон магнитоэлектрической индукции Фарадей вывел на основании экспериментов с магнитными полями, то эксперименты по установлению справедливости соотношения (1.17) в то время провести было невозможно, т.к. для проведения такого эксперимента не хватало чувствительности существующих измерительных приборов.
и второй член правой части исчезнут, и получим ток смещения, введенный Максвеллом. Но Максвелл ввел этот параметр, не прибегая к закону электромагнитной индукции (1.17). Если свой закон магнитоэлектрической индукции Фарадей вывел на основании экспериментов с магнитными полями, то эксперименты по установлению справедливости соотношения (1.17) в то время провести было невозможно, т.к. для проведения такого эксперимента не хватало чувствительности существующих измерительных приборов.
Для случая постоянных электрических полей из (1.19) получаем:
(1.20)
Динамические потенциалы и поля движущихся зарядов
Тот путь, который продемонстрирован в предыдущем разделе, касающийся введения полных производных полей, пройден в значительной части ещё Герцем, о чём подробно написано в работе [2]. Правда, Герц не вводил понятие векторных потенциалов, а оперировал только полями, но это не умаляет его заслуг. Герц ошибался лишь в том, что считал электрические и магнитные поля инвариантами скорости. Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами, а также электромагнитными волнами, которые генерируются неподвижными и движущимися источниками таких волн. Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
Как уже отмечалось, в классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной.
В данном разделе будет сделана попытка найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [3-5], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы, как показано в предыдущем разделе записываются следующим образом:
(2.1)
или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле  за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [3-5]:
(2.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
Именно такая зависимость скалярного потенциала заряда от его относительной скорости и отсутствовала ранее в классической электродинамике, что является главной её ошибкой.
Поскольку любой процесс распространения электрических полей и потенциалов всегда связан с запаздыванием, введём запаздывающий скалярно-векторный потенциал, считая, что поле этого потенциала распространяется в данной среде со скоростью света:
(2.5)
где  – составляющая скорости заряда
– составляющая скорости заряда ![]() , нормальная к вектору
, нормальная к вектору ![]() в момент времени
в момент времени 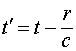 ,
, ![]() – расстояния между зарядом и точкой, в которой определяется поле, в момент времени
– расстояния между зарядом и точкой, в которой определяется поле, в момент времени ![]() .
.
Как показано в работах [3-5, 7] зависимость запаздывающего скалярного потенциала от скорости (2.5), являются основополагающим законом классической электродинамики, из которого следуют все остальные её законы. Более того, введение такого потенциала исключает необходимость введение в электродинамике такого понятия как магнитное поле. И это есть революция в современной физике.
Список литературы
- 1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.
- 2. Мандельштам Л. И. Лекции по оптике, теории относительности и квантовой механике. М: Наука, 1972. – 437 с.
- 3. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков,
Константа, 2003.- 72 с.
- 4. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- 5. Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- 6. Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 7. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.