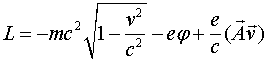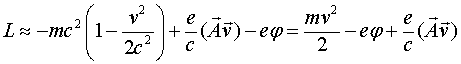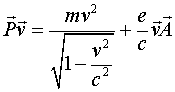В чём просчитались теоретики, введя обобщённый импульс движущегося заряда
В чём просчитались теоретики, введя обобщённый импульс движущегося заряда?
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: | |
В механике под функцией Лагранжа частицы понимают разницу между её кинетической и потенциальной энергией
(1)
Выражая кинетическую энергию через импульс ![]() , который характеризует кинетическое движение частицы, получаем
, который характеризует кинетическое движение частицы, получаем
(2)
Принцип наименьшего действия и Лагранжев формализм теоретики попытались распространить и на движущийся заряд. Дадим по этому поводу выдержку из хорошо известного курса по теоретической физике [1]:
«Уравнение движения приобретает вид
(23.9)
(в этом соотношении ![]() ,
, ![]() и
и ![]() - масса, заряд и скорость частицы,
- масса, заряд и скорость частицы, ![]() - скорость света,
- скорость света, ![]() и
и ![]() - скалярный и векторный потенциал).
- скалярный и векторный потенциал).
Это уравнение движения можно рассматривать как уравнение Лагранжа, если функция Лагранжа имеет вид
(23.10)
Действительно, при этом обобщённый импульс
(23.11)
Соответственно обобщённая сила
Уравнение Лагранжа гласит:
Или
(23.12)
Подстановка ![]() и
и ![]() в (23.12) вновь приводит нас к (23.9).
в (23.12) вновь приводит нас к (23.9).
В нерелятивистском приближении функция Лагранжа приобретает вид
(23.13)
При этом мы опустили постоянную ![]() , поскольку в уравнение Лагранжа входят лишь производные от
, поскольку в уравнение Лагранжа входят лишь производные от ![]() , а сама
, а сама ![]() определена лишь до полной производной по времени.
определена лишь до полной производной по времени.
Сравнивая функцию Лагранжа частицы в электромагнитном поле с выражением для функции Лагранжа в обычном поле сил
Мы видим, что при движении в поле функция Лагранжа содержит ещё член, зависящий от скорости и вектор-потенциала. Поэтому даже в нерелятивистском приближении функция Лагранжа в электромагнитном поле не может быть представлена в виде разности кинетической и потенциальной энергии». (конец цитаты).
Последняя фраза вызывает недоумение, из неё следует, что описание свойств заряда, движущегося в электромагнитном поле не может быть описано в рамках Лагранжева формализма т.к. она не является разностью кинетической и потенциальной энергии заряда, а следовательно к нему не может быть применён принцип наименьшего действия. В чём же дело?
Обратим внимание на то, как в данном случае вводится обобщённый импульс движущегося заряда (23.11), который должен характеризовать кинетическое движение и входить в формулу для вычисления кинетической энергии (2). Попробуем, пользуясь соотношением (23.11), получить значение кинетической энергии заряда, умножив обе его части скалярно на скорость.
(3)
Выражение (3) должно по определению составлять удвоенное значение кинетической энергии. Так ли это? Первый член правой части этого выражения действительно представляет кинетическую энергию релятивистского заряда. А что же представляет второй член правой части? Оказывается этот член никакая не кинетическая энергия. В работе http://fmnauka.narod.ru/Pro1.pdf показано, что второй член правой части выражения (3) представляет потенциальную энергию заряда, движущегося в поле векторного потенциала ![]() .
.
Таким образом, в современной теоретической физике допущена ошибка, когда в обобщённый импульс движущегося заряда, который должен характеризовать его кинетическую энергию, включена составляющая, которая характеризует потенциальную энергию заряда, связанную с его движением в поле векторного потенциала.
Литература
- Левич В. Г. Курс теоретической физики, том 1. Теория электромагнитного поля, теория относительности, статистическая физика, М: Физматгиз, 1962, 695 –с.
- Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.