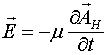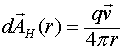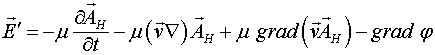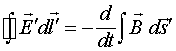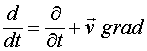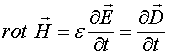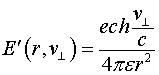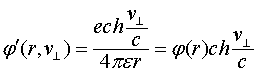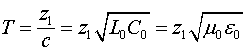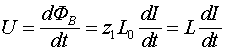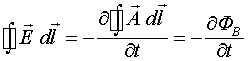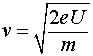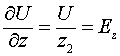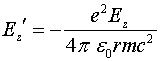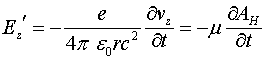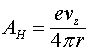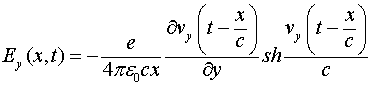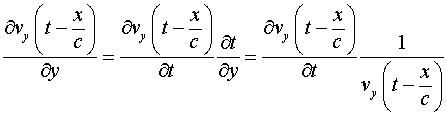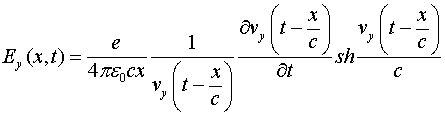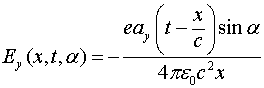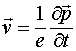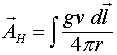Верен ли закон индукции Фарадея
Верен ли закон индукции Фарадея?
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: | |
Содержание
Введение
Магнитоэлектрический закон Фарадея, который является основным законом электродинамики, был сформулирован в начале позапрошлого века. Одним из основных понятий, которое фигурирует в этом законе, является магнитное поле, которое до этого было введено Ампером. Тогда ещё не было ни уравнений Максвелла, ни опытов Герца. Никто тогда не знал, что существуют электромагнитные волны, которые распространяются по длинным линиям со скоростью света. Не было также теории электрических цепей с распределёнными параметрами и телеграфных уравнений. Но, тем не менее, законом индукции Фарадея мы пользуемся до сих пор как основу всей электродинамики. И, естественно, возникает вопрос, а насколько точен этот закон и правильно ли он и полностью отражает законы индукции.
Законы индукции классической электродинамики
Исторически закон Фарадея в имеющейся литературе принято называть электромагнитным. Такое название не соответствует тому физическому процессу, который он описывает. Этот закон указывает на то, какое электрическое поле можно генерировать путём изменения магнитного поля, поэтому правильно его называть законом магнитоэлектрической индукции.
Основная задача законов индукции заключается в выяснении причин появления в пространстве электрических полей, а, следовательно, и сил действующих на заряд, в данной точке пространства, в данной ИСО. Это главная задача законов индукции, т.к. только электрические поля, генерируемые тем или иным способом, оказывают силовые воздействия на заряд. Такие поля могут возникать при изменении расположения других зарядов вокруг заданной точки пространства. Если вокруг рассматриваемой точки имеется какая-то статическая конфигурация зарядов, то напряженность электрического поля в этой точке будет определяться соотношением
где ![]() скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций. Если изменить расположение зарядов, то этой новой конфигурации будут соответствовать и другие значения скалярного потенциала, а, следовательно, и другие значения напряженности электрического поля. Но такое перемещение зарядов в пространстве в обязательном порядке сопряжено с их ускорением и последующим замедлением. Ускорение или замедление зарядов также может приводить к возникновению в окружающем пространстве электрических полей индукции.
скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций. Если изменить расположение зарядов, то этой новой конфигурации будут соответствовать и другие значения скалярного потенциала, а, следовательно, и другие значения напряженности электрического поля. Но такое перемещение зарядов в пространстве в обязательном порядке сопряжено с их ускорением и последующим замедлением. Ускорение или замедление зарядов также может приводить к возникновению в окружающем пространстве электрических полей индукции.
Основным законом индукции в классической электродинамике является закон Фарадея, который записывается следующим образом:
(1.1)
где ![]() - вектор магнитной индукции,
- вектор магнитной индукции, ![]() - поток магнитной индукции, а
- поток магнитной индукции, а ![]() - магнитная проницаемость среды.
- магнитная проницаемость среды.
Из этого закона следует, что циркуляция вектора электрического поля равна изменению потока магнитной индукции через площадку, которую охватывает данный контур. Сразу подчеркнём то обстоятельство, что рассматриваемый закон представляет процессы взаимной индукции, т.к. для получения циркуляции вектора ![]() берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.1) получают первое уравнение Максвелла
берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.1) получают первое уравнение Максвелла
(1.2)
Но здесь необходимо сделать одно замечание. Переход от интегральной формы (1.1) к дифференциальной форме (1.2) не вполне законен. Правомерность такого перехода справедлива только в том случае, когда контур интегрирования в левой части соотношения (1.1) охватывает площадь интегрирования в интеграле правой части. Но опыты, которые провел Фарадей, совсем не предполагают этого, контур интегрирования в левой части, а вернее проволока, в которой индуцировалась э.д.с., может не совпадать с границами площадки интегрирования в правой части. Главным условием соблюдения соотношения (1.1) являлось то, что контур интегрирования в правой части должен охватывать контур интегрирования в левой. Примером тому может служить случай длинного соленоида, когда поток индукции сосредоточен во внутренней его части, а контур интегрирования может проходить за его пределами, где магнитных полей нет. Важно только, чтобы контур интегрирования в левой части соотношения (1.1) охватывал соленоид.
Введём векторный потенциал ![]() , удовлетворяющий равенству
, удовлетворяющий равенству ![]() , где контур интегрирования совпадает с контуром интегрирования в соотношении (1.1), а вектор
, где контур интегрирования совпадает с контуром интегрирования в соотношении (1.1), а вектор ![]() определен на всех его участках, тогда
определен на всех его участках, тогда
(1.3)
Путём введения вектор ![]() обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора
обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора ![]() по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор
по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор ![]() , связан с магнитным полем соотношением:
, связан с магнитным полем соотношением:
(1.4)
Таким образом, вектор ![]() является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
Если имеется прямой проводник с током, то вокруг него образуется поле векторного потенциала, в этом случае ![]() и, следовательно, в окрестностях такого проводника возникает также и магнитное поле, которое изменяется при изменении тока в проводнике. Отрезок провода длиной
и, следовательно, в окрестностях такого проводника возникает также и магнитное поле, которое изменяется при изменении тока в проводнике. Отрезок провода длиной ![]() , по которому протекает ток
, по которому протекает ток ![]() , генерирует в дальней зоне (имеется в виду, что расстояние
, генерирует в дальней зоне (имеется в виду, что расстояние ![]() значительно больше длины отрезка) векторный потенциал
значительно больше длины отрезка) векторный потенциал
Это соотношение может быть переписано и по-другому:
где ![]() - заряд, приходящийся на единицу длины проводника, по которому протекает ток.
- заряд, приходящийся на единицу длины проводника, по которому протекает ток.
Отметим то обстоятельство, что векторный потенциал убывает, как ![]() , и по этому же закону, в соответствии с соотношением (1.3), убывают и индуцируемые электрические поля. Магнитные же поля, поскольку
, и по этому же закону, в соответствии с соотношением (1.3), убывают и индуцируемые электрические поля. Магнитные же поля, поскольку ![]() , убывают, как
, убывают, как ![]() , и при больших расстояниях ими можно пренебречь. Таким образом, на больших расстояниях закон индукции продолжает работать, однако, индуцируемые электрические поля уже полностью зависят только от векторного потенциала и, что очень важно, убывают они уже не по закону
, и при больших расстояниях ими можно пренебречь. Таким образом, на больших расстояниях закон индукции продолжает работать, однако, индуцируемые электрические поля уже полностью зависят только от векторного потенциала и, что очень важно, убывают они уже не по закону ![]() , как в случае скалярного потенциала, а как
, как в случае скалярного потенциала, а как ![]() , что характерно для излучающих систем.
, что характерно для излучающих систем.
До сих пор решение вопроса о возникновении электрических полей в движущихся системах можно было осуществлять двумя путями. Первый - заключался в вычислении силы Лоренца, действующей на движущиеся заряды, второй путь заключался в измерении изменения магнитного потока через исследуемый контур. Оба метода давали одинаковый результат. Это было непонятно, и уже приводилось по этому поводу высказывания авторов работы [1]. В связи с непониманием физической природы такого положения дел и начали считать, что униполярный генератор является исключением из правила потока [1]. Рассмотрим эту ситуацию подробнее.
Для того чтобы ответить на поставленный вопрос, следует несколько изменить соотношение (1.3), заменив в нём частную производную на полную:
(1.5)
Штрих около вектора ![]() означает, что это поле определяется в движущейся системе координат, в то время как вектор
означает, что это поле определяется в движущейся системе координат, в то время как вектор ![]() определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.5) можно переписать следующим образом:
определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.5) можно переписать следующим образом:
где ![]() - скорость штрихованной системы.
- скорость штрихованной системы.
Следовательно, дополнительная сила, действующая на заряд в движущейся системе, запишется
Эта сила зависит только от пространственных производных векторного потенциала и скорости штрихованной системы.
Заряд, движущийся в поле векторного потенциала ![]() со скоростью
со скоростью ![]() , обладает также потенциальной энергией [1]
, обладает также потенциальной энергией [1]
Поэтому должна существовать еще одна сила, действующая на заряд в движущейся ИСО, а именно:
Таким образом, величина ![]() играет такую же роль, что и скалярный потенциал
играет такую же роль, что и скалярный потенциал ![]() , градиент которого дает электрическое поле. Следовательно, суммарная сила, которая действует на заряд, движущийся в поле векторного потенциала, может иметь три составляющие и запишется как
, градиент которого дает электрическое поле. Следовательно, суммарная сила, которая действует на заряд, движущийся в поле векторного потенциала, может иметь три составляющие и запишется как
(1.6)
Первая из составляющих этой силы действует на неподвижный заряд, когда векторный потенциал имеет локальную производную по времени. Вторая составляющая также определяет изменения векторного потенциала во времени, но они связаны уже с движением заряда в пространственно меняющемся поле этого потенциала. Совсем иная природа у силы, которая определяется последним слагаемым соотношения (1.6). Она связана с тем, что заряд, двигающийся в поле векторного потенциала, обладает потенциальной энергией, градиент которой и дает силу. Из соотношения (1.6) следует
(1.7)
Это и есть полный закон взаимной индукции. Он определяет все электрические поля, которые могут возникать в заданной точке пространства, причем эта точка может быть как неподвижной, так и движущейся. Этот единый закон включает в себя и закон Фарадея, и ту часть силы Лоренца, которая связана с движением заряда в магнитном поле. Этот закон без всяких исключений дает ответ на все вопросы, касающиеся взаимной магнитоэлектрической индукции. Показательно, что, если взять ротор от обеих частей равенства (1.7), пытаясь получить первое уравнение Максвелла, то сразу будет потеряна существенная часть информации, т.к. ротор от градиента тождественно равен нулю.
Если выделить те силы, которые связаны с движением заряда в поле векторного потенциала, и учесть, что
то из (1.6) получим
(1.8)
Учитывая (1.4), запишем:
(1.9)
Или
(1.10)
Окончательно:
(1.11)
Может показаться, что соотношение (1.11) представляет силу Лоренца, однако, это не так. В этом соотношении и поле ![]() , и поле
, и поле ![]() являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.11) добавить слагаемое
являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.11) добавить слагаемое ![]() :
:
где ![]() - скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
- скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
Теперь соотношение (1.7) можно переписать следующим образом:
(1.12)
или, собрав первые два члена в полную производную векторного потенциала по времени, и, внеся под знак градиента два последних члена правой части соотношения (1.12), получим:
(1.13)
Если обе части соотношения (1.13) умножить на величину заряда, то можно получить полную силу, действующую на заряд. От силы Лоренца она будет отличаться силой  . Из соотношения (1.13) видно, что величина
. Из соотношения (1.13) видно, что величина ![]() играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (13) и учесть, что
играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (13) и учесть, что ![]() , то получим:
, то получим:
Если в данном соотношении заменить полную производную на частную, т.е. считать, что поля определяются только в заданной инерциальной системе, то получим первое уравнение Максвелла.
Ранее сила Лоренца рассматривалась как фундаментальный опытный факт, не связанный с законом индукции. Расчетным путем получить последнее слагаемое правой части соотношения (1.11) можно было только в рамках СТО. В данном случае все слагаемые соотношение (1.11) получены из закона индукции в рамках преобразований Галилея. Причем соотношение (1.11) это и есть полный закон взаимной индукции, если его записать в терминах векторного потенциала. Это есть как раз то правило, которое дает возможность, зная поля в одной ИСО, вычислять поля в другой инерциальной системе, и этого правила до сих пор не было в классической электродинамике. Но такой подход вовсе не проливает свет на физическую причину возникновения векторного потенциала, т.к. он, как и магнитное поле вводится феноменологическим путём.
Сам Фарадей при проведении своих опытов установил, что в контуре индуцируется ток, когда в соседнем контуре включается или выключается постоянный ток, или соседний контур с постоянным током движется относительно первого контура. Поэтому в общем виде закон Фарадея следует записать следующим образом:
(1.14)
Данная запись закона указывает на то, что при записи циркуляции вектора ![]() в движущейся (штрихованной) системе координат, около
в движущейся (штрихованной) системе координат, около ![]() и
и ![]() следует ставить штрихи, указывающие на тот, что поток определён в одной ИСО, а поля в другой. Если же циркуляция определяется только в заданной ИСО, то штрихи около
следует ставить штрихи, указывающие на тот, что поток определён в одной ИСО, а поля в другой. Если же циркуляция определяется только в заданной ИСО, то штрихи около ![]() и
и ![]() отсутствуют, но при этом справа в выражении (1.14) должна стоять частная производная по времени.
отсутствуют, но при этом справа в выражении (1.14) должна стоять частная производная по времени.
Полная производная по времени в соотношении (1.14) означает независимость конечного результата появления э.д.с. в контуре от способа изменения потока. Поток может изменяться как за счет локальной производной магнитного потока по времени, так и за счет того, что ИСО, в которой измеряется циркуляция ![]() , движется в пространственно меняющемся поле
, движется в пространственно меняющемся поле ![]() . Величину магнитного потока в соотношении (1.14) вычисляем при помощи выражения:
. Величину магнитного потока в соотношении (1.14) вычисляем при помощи выражения:
(1.15)
где магнитная индукция ![]() определена в неподвижной системе координат, а элемент
определена в неподвижной системе координат, а элемент ![]() определен в движущейся системе.
определен в движущейся системе.
Учитывая (1.14), из (1.15) получаем:
(1.16)
В данном случае контурный интеграл берется по контуру ![]() , охватывающему площадку
, охватывающему площадку![]() . Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е.
. Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е. ![]() и
и ![]() . Поскольку
. Поскольку![]() , из (16) получаем соотношение
, из (16) получаем соотношение
(1.17)
Из соотношения (1.17) следует, что при движении в магнитном поле возникает дополнительное электрическое поле, определяемое последним слагаемым этого соотношения. Заметим, что данное соотношение получено не путем введения силы Лоренца аксиоматическим способом или из ковариантных преобразований Лоренца, а непосредственно из закона Фарадея, причем в рамках преобразований Галилея. Таким образом, сила Лоренца является прямым следствием закона магнитоэлектрической индукции.
Закон Фарадея показывает, каким образом изменение магнитных полей приводит к появлению электрических полей. Однако возникает вопрос о том, приводит ли изменение электрических полей к возникновению каких-либо других полей и, в частности, магнитных? Ответ на этот вопрос дал Максвелл, введя ток смещения в свое второе уравнение. В случае отсутствия токов проводимости второе уравнение Максвелла выглядит следующим образом:
От этого соотношения нетрудно перейти к выражению
(1.18)
где ![]() поток электрической индукции.
поток электрической индукции.
Однако для полного описания процессов взаимной электрической индукции соотношения (1.18) недостаточно. Как и в случае закона Фарадея, следует учесть то обстоятельство, что поток электрической индукции может меняться не только за счет локальной производной электрического поля по времени, но и за счет того, что контур, вдоль которого производится интегрирование, может двигаться в пространственно меняющемся электрическом поле. Это означает, что в соотношении (1.18), как и в случае закона Фарадея, следует заменить частную производную на полную. Обозначая штрихами поля и элементы контура в движущейся ИСО, получим:
и далее
(1.19)
Для электронейтральной среды ![]() , поэтому последний член правой части в этом выражении будет отсутствовать. Для этого случая соотношение (1.19) будет иметь вид:
, поэтому последний член правой части в этом выражении будет отсутствовать. Для этого случая соотношение (1.19) будет иметь вид:
(1.20)
Если в этом соотношении перейти от интегрирования по контуру к интегрированию по поверхности, то получим:
(1.21)
Из (1.21) получаем
(1.22)
Если, исходя из этого соотношения, записать поля в данной инерциальной системе, то штрих около ![]() и второй член правой части исчезнут, и получим ток смещения, введенный Максвеллом. Но Максвелл ввел этот параметр, не прибегая к закону электромагнитной индукции (1.19). Если свой закон магнитоэлектрической индукции Фарадей вывел на основании экспериментов с магнитными полями, то эксперименты по установлению справедливости соотношения (1.19) в то время провести было невозможно, т.к. для проведения такого эксперимента не хватало чувствительности существующих измерительных приборов.
и второй член правой части исчезнут, и получим ток смещения, введенный Максвеллом. Но Максвелл ввел этот параметр, не прибегая к закону электромагнитной индукции (1.19). Если свой закон магнитоэлектрической индукции Фарадей вывел на основании экспериментов с магнитными полями, то эксперименты по установлению справедливости соотношения (1.19) в то время провести было невозможно, т.к. для проведения такого эксперимента не хватало чувствительности существующих измерительных приборов.
Динамические потенциалы и поля движущихся зарядов
Находясь в заданной ИСО, нас интересуют те поля, которые создаются в ней неподвижными и движущимися зарядами, а также электромагнитными волнами, которые генерируются неподвижными и движущимися источниками таких волн. Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
Как уже отмечалось, в классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной [2].
В данном разделе будет сделана попытка найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [3-5], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы, как показано в предыдущей главе записываются следующим образом:
(2.1)
Или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [6]. Электрическое поле  за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда ![]() , то его электрическое поле будет определяться соотношением:
, то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом [3-5]:
(2.4)
где ![]() - скалярный потенциал неподвижного заряда.
- скалярный потенциал неподвижного заряда.
Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
Соотношение (2.4) является следствием двух законов индукции, рассмотренных выше, но нам по-прежнему неясна физическая природа возникновения магнитного векторного потенциала, а следовательно и электрических полей индукции, возникающих при протекании токов по проводникам. Однако из экспериментов нам известно, что электрические поля индукции, всегда направлены противоположно тем, которые ускоряют электроны проводимости в проводниках.
Переходные процессы в отрезках длинных линий
Теперь рассмотрим вопрос о том, как будут работать правила потоков на отрезках длинных линий с распределенными параметрами, которые могут представлять или индуктивность (линия закороченная на конце) или емкость (разомкнутая линия).
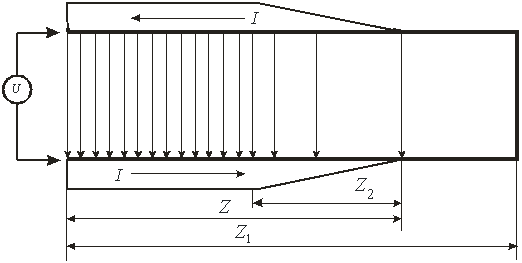
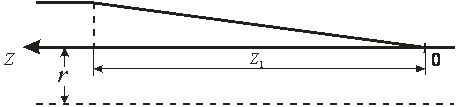
Закоротим линию на расстоянии ![]() от ее начала (рис. 1).
от ее начала (рис. 1).
Рис. 1. Распространение волны тока и напряжения в длинной линии.
Очевидно, что суммарная индуктивность линии при этом составит величину  . Если подключить к линии источник постоянного напряжения, в ней начнет распространяться волна тока
. Если подключить к линии источник постоянного напряжения, в ней начнет распространяться волна тока 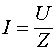 и напряжения
и напряжения ![]() . В тот момент, когда на коротком замыкании, на котором имеет место граничное условие
. В тот момент, когда на коротком замыкании, на котором имеет место граничное условие ![]() , появляется падающая волна с напряжением
, появляется падающая волна с напряжением ![]() , возникает отраженная волна с напряжением
, возникает отраженная волна с напряжением ![]() , бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен
, бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен  , т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный
, т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный ![]() , и нулевое напряжение. Когда отраженная волна возвратиться к началу линии, она принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию волну напряжения
, и нулевое напряжение. Когда отраженная волна возвратиться к началу линии, она принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию волну напряжения ![]() и ток
и ток ![]() . Этот ток сложиться с током
. Этот ток сложиться с током ![]() , и суммарный ток в линии составит
, и суммарный ток в линии составит ![]() . Ток и далее будет нарастать ступеньками, добавляя каждый раз к своему прежнему значению величину
. Ток и далее будет нарастать ступеньками, добавляя каждый раз к своему прежнему значению величину ![]() . Если отобразить этот процесс во времени, то он будет выглядеть, как показано на рис. 2.
. Если отобразить этот процесс во времени, то он будет выглядеть, как показано на рис. 2.
Рис. 2. График зависимости входного тока от времени для закороченной линии.
На этом рисунке время
соответствует времени, за которое волна пробегает по линии в одну сторону.
На рис. 1 волна тока в правой своей части на участке ![]() имеет скос. Этот участок соответствует времени переходного процесса
имеет скос. Этот участок соответствует времени переходного процесса  , за которое напряжение подключаемого к линии источника достигает своего номинального значения. На этом же участке и ток в линии, и электрическое поле меняет свою величину от нулевого значения до номинального. Очевидно, что именно на этом участке скорость носителей тока меняется от нулевого значения в начале скоса до своего номинального значения в его конце.
, за которое напряжение подключаемого к линии источника достигает своего номинального значения. На этом же участке и ток в линии, и электрическое поле меняет свою величину от нулевого значения до номинального. Очевидно, что именно на этом участке скорость носителей тока меняется от нулевого значения в начале скоса до своего номинального значения в его конце.
Следует обратить внимание на то, что, как видно из рис. 3, мощность, отбираемая закороченной линией у источника напряжения, не является линейной функцией, а по истечении времени равному ![]() скачком увеличивается на
скачком увеличивается на ![]() , причем первый скачек равен
, причем первый скачек равен ![]() . Нетрудно показать, что магнитный поток в данном случае изменяется по линейному закону (рис. 3).
. Нетрудно показать, что магнитный поток в данном случае изменяется по линейному закону (рис. 3).
Действительно, при прямом ходе волны до момента времени ![]() , когда волна достигнет закороченного участка, поток будет увеличиваться по линейному закону и к моменту
, когда волна достигнет закороченного участка, поток будет увеличиваться по линейному закону и к моменту ![]() достигнет величины
достигнет величины  . Когда, отразившись от закоротки, волна начнет двигаться в обратном направлении, то поток снова будет возрастать по линейному закону и к моменту прихода волны к источнику напряжения достигнет величины
. Когда, отразившись от закоротки, волна начнет двигаться в обратном направлении, то поток снова будет возрастать по линейному закону и к моменту прихода волны к источнику напряжения достигнет величины  .
.
Таким образом, в режиме самоиндукции, как и в случае подключения к источнику питания бесконечно длинной линии, выполняется соотношение
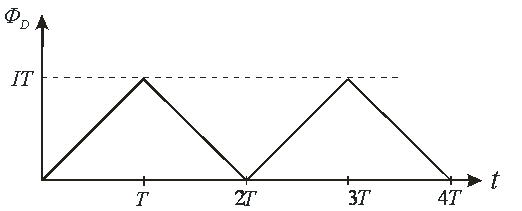
Электрический поток в линии тоже будет изменяться по определенному закону (рис. 4).
Рис. 3. Зависимость магнитного потока от времени для закороченной линии.
Рис. 4. Зависимость электрического потока от времени для закороченной линии.
В отличие от магнитного потока он будет изменяться периодически, то, возрастая, то, убывая, по линейному закону. Когда волна движется в положительном направлении, одновременно возрастает и магнитный и электрический поток. При этом как в магнитном, так и в электрическом поле запасаемая энергия возрастает. Когда волна начинает двигаться в обратном направлении, то электрическое поле начинает исчезать, а его энергия переходит в магнитную энергию обратной волны тока.
После достижения волной источника питания магнитное поле удваивается по своей величине, а электрическое поле в линии исчезает. Далее цикл повторяется. Следовательно, процессу возрастания магнитного потока в индуктивности, в обязательном порядке сопутствует процесс периодического изменения потока электрической индукции, при котором между плоскостями линии периодически возникает и исчезает электрическое поле.
Теперь рассмотрим вопрос о взаимной индукции, когда в исходной короткозамкнутой длинной линии находиться отрезок другой длинной линии меньших размеров. Расположим между плоскостями короткозамкнутой линии короткозамкнутый с обоих концов отрезок другой линии такой же ширины, но с расстоянием ![]() <<
<<![]() (рис. 5).
(рис. 5).
Рис. 5. Процессы взаимной индукции в закороченной линии.
Будем считать, что короткозамкнутый отрезок выполнен из сверхпроводника, и токи, возбуждаемые в нем, затухать не могут. Если подключить к линии источник напряжения, то по линии начнет распространяться волна, в которой напряжение источника и ток в линии связаны соотношением 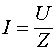 . Когда волна напряжения достигнет перемычки вложенной линии, то к ней будет приложено напряжение
. Когда волна напряжения достигнет перемычки вложенной линии, то к ней будет приложено напряжение 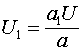 . На короткозамыкающей перемычке выполняется граничное условие
. На короткозамыкающей перемычке выполняется граничное условие ![]() , поэтому на ней возникнет напряжение обратное
, поэтому на ней возникнет напряжение обратное ![]() , в связи с этим по перемычке начнут двигаться заряды в направлении указанном стрелкой. Минуя короткозамкнутую перемычку, волна уже будет двигаться не по одной, а по двум параллельным линиям и токи, текущие по элементам вложенной линии будут течь в направлении, которое является обратным направлению токам в проводниках основной линии. И вот здесь, несмотря на всю очевидность происходящего, возникает один важный вопрос. Действительно, очевидным является то, что токи во вставной линии текут в обратном направлении по отношению к основной линии. Но для того, чтобы эти токи начали течь, необходимо, чтобы в области фронта распространяющейся волны заряды во вставной линии ускорялись. Но для того, чтобы заряды ускорялись, необходимо наличие тангенциальной составляющей электрического поля на плоскостях вставной линии, в то же время в нашем распоряжении имеются только нормальные составляющие этого поля. На рис. 1 мы уже показали тот участок основной линии, где происходит ускорение свободных зарядов. Этот участок двигается по основной линии со скоростью света, и именно к этому участку приложено напряжение источника питания, ускоряющее носители тока. Ток во вставной линии двигается в обратном направлении и имеет такую же величину что и в основной линии. Значит в области фронта двигающейся волны на проводящих плоскостях вставной линии необходимо наличие тангенциальной составляющей электрического поля, обратного тому полю, которое ускоряет заряды в основной линии. Да это именно так, но у нас нет пока физических причин, которые смогли бы объяснить появление такого поля. Как раз это и есть основной вопрос индукции. В пятой главе мы подробно рассмотрим этот вопрос и покажем истинные причины появления таких полей, и читатель сможет убедиться, что причиной их появления является не закон Фарадея.
, в связи с этим по перемычке начнут двигаться заряды в направлении указанном стрелкой. Минуя короткозамкнутую перемычку, волна уже будет двигаться не по одной, а по двум параллельным линиям и токи, текущие по элементам вложенной линии будут течь в направлении, которое является обратным направлению токам в проводниках основной линии. И вот здесь, несмотря на всю очевидность происходящего, возникает один важный вопрос. Действительно, очевидным является то, что токи во вставной линии текут в обратном направлении по отношению к основной линии. Но для того, чтобы эти токи начали течь, необходимо, чтобы в области фронта распространяющейся волны заряды во вставной линии ускорялись. Но для того, чтобы заряды ускорялись, необходимо наличие тангенциальной составляющей электрического поля на плоскостях вставной линии, в то же время в нашем распоряжении имеются только нормальные составляющие этого поля. На рис. 1 мы уже показали тот участок основной линии, где происходит ускорение свободных зарядов. Этот участок двигается по основной линии со скоростью света, и именно к этому участку приложено напряжение источника питания, ускоряющее носители тока. Ток во вставной линии двигается в обратном направлении и имеет такую же величину что и в основной линии. Значит в области фронта двигающейся волны на проводящих плоскостях вставной линии необходимо наличие тангенциальной составляющей электрического поля, обратного тому полю, которое ускоряет заряды в основной линии. Да это именно так, но у нас нет пока физических причин, которые смогли бы объяснить появление такого поля. Как раз это и есть основной вопрос индукции. В пятой главе мы подробно рассмотрим этот вопрос и покажем истинные причины появления таких полей, и читатель сможет убедиться, что причиной их появления является не закон Фарадея.
В том случае, если возбуждаемые во вложенной линии токи не затухают, они будут двигаться вслед за электрическими полями. Когда волна минует вложенную линию, то в этой линии останутся незатухающие токи, которые полностью скомпенсируют в ее внутренней полости магнитное поле, а поляризационные заряды, наведенные внешним электрическим полем, полностью скомпенсируют внутри вставной линии электрическое поле. Таким образом, во внутренней части вложенной линии будут отсутствовать как магнитные, так и электрические поля.
В том же случае, если проводники вложенной линии имеют сопротивление, токи, индуцированные в ней, через некоторое время затухнут и в ее внутреннюю полость проникнет магнитное поле, которое по своей величине будет таким же, как и в основной линии. Но электрическое поле во внутреннюю полость проникнуть не сможет, т.к. на противоположных проводящих проводниках вложенной линии наведенные поляризационные заряды останутся. Таким образом, мы видим, что проникновение во внутреннюю часть вложенной линии магнитного потока обязательно обусловлено наличием потерь в проводниках этой линии. Очевидно, что данному процессу обязательно сопутствуют тепловые омические потери. Но конечный вариант, который мы получили, по сравнению с линией без вставки по-прежнему отличается тем, что электрическое поле, присутствующее в остальных частях основной линии, внутри вложенной линии отсутствует. Но установлению такой ситуации предшествовали тепловые омические потери в элементах вставной линии. Оказывается, что эти потери в точности соответствуют величине
(3.1)
т.е. той электростатической энергии, которая не проникла внутрь вложенной линии. Можем ли мы сделать так, чтобы при наличии полей в основной линии внутри полости, занимаемой вставной линией появилось электрическое поле? Для этого нужно отсоединить от вставной линии короткозамыкающие перемычки. Но при этом поляризационные заряды на противоположных проводниках вставной линии останутся и по-прежнему будут компенсировать электрические поля основной линии. Чтобы устранить такую компенсацию нужно сблизить плоскости вставной лини, доведя размер ![]() до нуля, таким образом, практически уничтожив влияние вставной линии на поля основной линии. При этом также будет израсходована работа, определяемая соотношением (3.1). Т.е. когда создавалась ситуация, при которой внутри вставной линии отсутствовали электрические поля, не была затрачена работа, определяемая соотношением (3.1). Теперь же, когда мы возвратились к нулевому варианту, эти затраты оказались возмещенными.
до нуля, таким образом, практически уничтожив влияние вставной линии на поля основной линии. При этом также будет израсходована работа, определяемая соотношением (3.1). Т.е. когда создавалась ситуация, при которой внутри вставной линии отсутствовали электрические поля, не была затрачена работа, определяемая соотношением (3.1). Теперь же, когда мы возвратились к нулевому варианту, эти затраты оказались возмещенными.
Теперь мы можем установить причины и правила взаимной индукции. Токи во вторичном контуре, связанного индуктивно с первичным (генерирующим) контуром, возбуждает не изменение магнитного потока через вторичный контур, а электрические поля первичного контура. При этом во вторичном контуре генерируются токи обратные по направлению токам первичного контура, а магнитные поля, генерируемые этими токами, направлены против полей первичного контура. При этом магнитный поток вторичного контура ![]() остается равным нулю, если вторичный контур не имеет активного сопротивления. Изменение магнитного потока вторичного контура возможно только при наличии в его проводящих элементах активных потерь. При этом будет выполняться равенство
остается равным нулю, если вторичный контур не имеет активного сопротивления. Изменение магнитного потока вторичного контура возможно только при наличии в его проводящих элементах активных потерь. При этом будет выполняться равенство
Уменьшение компенсирующего потока вторичного контура в случае наличия активных потерь, приведет к возрастанию потока первичного контура ![]() , пронизывающего вторичный контур. Но, поскольку
, пронизывающего вторичный контур. Но, поскольку ![]() , то
, то
Т.е., если речь идет о самоиндукции, то знак электрического поля совпадает со знаком производной потока по времени. В случае же взаимной индукции, знаки электрического поля во вторичном контуре и производной внешнего магнитного потока разные. Таким образом, мы установили, что действительной причиной индуцирования токов в материальных структурах, расположенных в изменяющихся магнитных полях является не изменение потока, а движущиеся электрические поля индуцирующей структуры. Однако, формально циркуляция вектора электрического поля совпадает с производной потока магнитной индукции по времени.
Но раз мы приняли концепцию того, что токи во вторичном контуре генерирует не изменение магнитного потока, а движущиеся электрические поля первичного контура, то мы приходим к парадоксальной ситуации. Ведь снаружи рассматриваемой нами линии, если не считать краевых эффектов, электрических полей нет. Значить, если разместить вставную линию таким образом, чтобы она находилась не внутри первичной линии, а охватывала ее снаружи, то в ней не будут индуцироватся токи при возрастании потока в первичной линии, Если это так, то это входит в противоречие с законом индукции Фарадея. Так ли это? Это действительно так. Этот случай представлен на рис. 5. Возьмем первичную (индуцирующую) линию достаточной ширины и вторичную линию, ширина которой значительно меньше ширины первичной линии, причем сделаем так, чтобы вторичная линия охватывала первичную. Если теперь подключить источник переменного напряжения к первичной линии, то в ней начнет изменяться магнитный поток, и, поскольку этот же поток охватывает и вторичная линия, то казалось бы вольтметр, подсоединенный к вторичной линии должен зарегистрировать напряжение равное производной этого потока по времени. Но в приведенной схеме эксперимента вольтметр ничего не показывает. Если же вторичный контур, расположить внутри первичного контура, как показано на рис. 6, то при подключению к первичному контуру источника переменного напряжения, вольтметр, подключенный к вторичному контуру, показывает напряжение в соответствии с сформулированными выше правилами индукции. Как видно, мы имеем еще одно исключение из правила потока. Следовательно, мы должны заключить, что в области расположения вторичной линии на рис. 6, несмотря на изменение магнитного потока через поперечное сечение первичной линии, нет полей векторного потенциала.
Рис. 6. Схема взаимной индукции между контурами с внутренним расположением индуцирующего контура.
Рис.7. Схема взаимной индукции между контурами с внешним расположением индуцирующего контура.
Имеется еще один случай подтверждающий несостоятельность введения циркуляции векторного потенциала вокруг цилиндрических токонесущих систем. По существующим представлениям, если имеется цилиндрическая токонесущая система, например длинный соленоид, или длинный сверхпроводящий цилиндр, то вокруг них имеются циркуляция векторного потенциала. Поскольку
(3.2)
то при изменении тока в соленоиде или цилиндре будет меняться поток ![]() , а, следовательно, в проводящей петле, охватывающей соленоид или цилиндр, будет индуцироваться ток. Если такую петлю разорвать и подключить в месте разрыва вольтметр, то при изменении тока в соленоиде или цилиндре он должен в соответствии с соотношением (3.2) показывать индуцированное напряжение. Если проводить эксперименты с соленоидом, то имеется полное соответствие с соотношением (3.2). Для цилиндрического же образца правило индукции не выполняется и в петле его окружающей е.д.с. не индуцируется.
, а, следовательно, в проводящей петле, охватывающей соленоид или цилиндр, будет индуцироваться ток. Если такую петлю разорвать и подключить в месте разрыва вольтметр, то при изменении тока в соленоиде или цилиндре он должен в соответствии с соотношением (3.2) показывать индуцированное напряжение. Если проводить эксперименты с соленоидом, то имеется полное соответствие с соотношением (3.2). Для цилиндрического же образца правило индукции не выполняется и в петле его окружающей е.д.с. не индуцируется.
Для выяснения причин такого парадокса рассмотрим вопрос возникновения электрических полей вокруг длинного соленоида при подключении к нему источника напряжения. Мы уже высказывали сомнение по поводу возможности того, что магнитное поле внутри длинного соленоида при подключении к нему источника питания может возрастать синхронно на протяжении всей его длины. Рассмотрим конкретную схему подключения к длинному соленоиду источника напряжения (рис. 8).
Рис. 8. Схема распространения магнитных полей в длинном соленоиде
В данном случае мы имеем дело с длинной линией, одним из проводников которой является соленоид. Погонная индуктивность у такого соленоида может быть гораздо больше, чем у прямого провода, следовательно, такая линия будет иметь большое волновое сопротивление, а волна в ней будет распространяться медленнее, чем в свободном пространстве. Но процессы распространения в такой линии ничем не будут отличаться от процессов рассмотренных выше.
Когда в этой линии волна дойдет до точки с координатой ![]() , то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой
, то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой ![]() . Когда волна дойдет до конца соленоида, то магнитным полем заполниться весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида. Положим теперь, что мы в определенном месте охватили соленоид витком и подключили к нему вольтметр. Напряжение в витке будет индуцироваться только в момент пересечения магнитным полем соленоида окрестностей поперечного сечения, вокруг которого расположен виток. Этот момент будет наступать как при прямом, так и при обратном ходе волны, причем полярность импульсов индуцируемого в витке напряжения в обоих случаях будет одна и та же. Частота импульсов будет зависеть от длины соленоида, и будет тем больше, чем короче соленоид. Следовательно, среднее значение индуцированного напряжения будет расти с уменьшением длины соленоида, т.е. его количества витков. Мы знаем, что коэффициент трансформации трансформатора как раз и определяется соотношением витков первичной и вторичной обмоток. Таким образом, сам процесс трансформации происходит совсем не так, как мы представляли его себе раньше, когда мы полагали, что магнитное поле в соленоиде нарастает плавно и синхронно во всех его поперечных сечениях. И у нас нет теперь никаких оснований говорить о том, что вокруг длинного соленоида на всем его протяжении (впрочем, как и вокруг длинного проводящего цилиндра), при протекании через них постоянного тока существует циркуляция векторного потенциала. Но как же тогда быть с опытами Бома и Аронова, которые такой потенциал обнаружили экспериментально [1]?
. Когда волна дойдет до конца соленоида, то магнитным полем заполниться весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида. Положим теперь, что мы в определенном месте охватили соленоид витком и подключили к нему вольтметр. Напряжение в витке будет индуцироваться только в момент пересечения магнитным полем соленоида окрестностей поперечного сечения, вокруг которого расположен виток. Этот момент будет наступать как при прямом, так и при обратном ходе волны, причем полярность импульсов индуцируемого в витке напряжения в обоих случаях будет одна и та же. Частота импульсов будет зависеть от длины соленоида, и будет тем больше, чем короче соленоид. Следовательно, среднее значение индуцированного напряжения будет расти с уменьшением длины соленоида, т.е. его количества витков. Мы знаем, что коэффициент трансформации трансформатора как раз и определяется соотношением витков первичной и вторичной обмоток. Таким образом, сам процесс трансформации происходит совсем не так, как мы представляли его себе раньше, когда мы полагали, что магнитное поле в соленоиде нарастает плавно и синхронно во всех его поперечных сечениях. И у нас нет теперь никаких оснований говорить о том, что вокруг длинного соленоида на всем его протяжении (впрочем, как и вокруг длинного проводящего цилиндра), при протекании через них постоянного тока существует циркуляция векторного потенциала. Но как же тогда быть с опытами Бома и Аронова, которые такой потенциал обнаружили экспериментально [1]?
Закон электро-электрической индукции и запаздывающие потенциалы
Ранее мы уже указывали на то, что решение задач взаимодействия движущихся зарядов в классической электродинамике мы решаем путем введения магнитного поля или векторного потенциала, которые являются полями посредниками. На движущийся или неподвижный заряд силовое действие может оказывать только электрическое поле. Поэтому возникает естественный вопрос, а нельзя ли установить законы прямого действия минуя поля посредники, которые давали бы ответ о прямом взаимодействии движущихся и неподвижных зарядов. Такой подход сразу давал бы ответ и об источниках и местах приложения сил действия и противодействия. Сейчас мы покажем, что применение скалярно-векторного потенциала дает возможность установить и прямые законы индукции, когда непосредственно свойства движущегося заряда без участия каких-либо вспомогательных полей дают возможность вычислить электрические поля индукции, генерируемые движущимся зарядом.
Рассмотрим диаграмму распространения тока и напряжения в отрезке длинной линии, представленной на рис. 1. На этом рисунке сам фронт волны показан скошенным и занимает отрезок линии длинной ![]() , следовательно, время такого переходного процесса равно
, следовательно, время такого переходного процесса равно 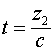 . Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который мы не смогли дать ответ ранее и на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время
. Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который мы не смогли дать ответ ранее и на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время ![]() достгает своего максимального значения
достгает своего максимального значения ![]() , после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок
, после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок ![]() . Изобразим этот участок отдельно, как показано на рис. 9.
. Изобразим этот участок отдельно, как показано на рис. 9.
Рис. 9. Фронт волны тока, распространяющейся в длинной линии
На участке ![]() происходит ускорение зарядов от их нулевой скорости (правее участка
происходит ускорение зарядов от их нулевой скорости (правее участка ![]() ) до значения скорости, определяемого соотношением
) до значения скорости, определяемого соотношением
где ![]() и
и ![]() - заряд и масса носителей тока, а
- заряд и масса носителей тока, а ![]() - падение напряжения на участке
- падение напряжения на участке ![]() . Тогда зависимость скорости носителей тока от координаты будет иметь вид:
. Тогда зависимость скорости носителей тока от координаты будет иметь вид:
(4.1)
Поскольку мы приняли линейную зависимость напряжения от времени на входе линии, то имеет место равенство
где ![]() - напряженность поля, ускоряющая заряды на участке
- напряженность поля, ускоряющая заряды на участке ![]() . Следовательно, соотношение (4.1) мы можем переписать
. Следовательно, соотношение (4.1) мы можем переписать
Теперь, используя соотношение (2.4) для величины салярно-векторного потенциала, вычислим его значение как функцию ![]() на некотором расстоянии
на некотором расстоянии ![]() от линии
от линии
(4.2)
При записи этого соотношения использовались только первые два члена разложения в ряд гиперболического косинуса.
Пользуясь формулой ![]() , и продифференцировав соотношение (4.2) по
, и продифференцировав соотношение (4.2) по ![]() , получаем
, получаем
(4.3)
где ![]() - электрическое поле, индуцируемое на расстоянии
- электрическое поле, индуцируемое на расстоянии ![]() от проводника линии. Около
от проводника линии. Около ![]() мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружаюших линию проводниках индукционные токи. Мы знаем, что ускорение
мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружаюших линию проводниках индукционные токи. Мы знаем, что ускорение ![]() , испытуемое зарядом
, испытуемое зарядом ![]() в поле
в поле ![]() , определяется соотношением
, определяется соотношением 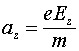 . С учетом этого из (4.3) получаем
. С учетом этого из (4.3) получаем
(4.4)
Таким образом, заряды, ускоряемые в отрезке линии ![]() , индуцируют на расстоянии
, индуцируют на расстоянии ![]() от этого участка электрическое поле, определяемое соотношением (4.4). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Мы получили закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Этот закон мы можем называть законом электро-электрической индукции, так как он, минуя поля посредники (магнитное поле или векторный потенциал), дает прямой ответ на то, какие электрические поля генерирует вокруг себя движущийся электрический заряд. Данный закон дает также ответ о месте приложения сил взаимодействия между зарядами. Именно это соотношение, а не закон Фарадея, мы должны считать основным законом индукции, т.к. именно оно устанавливает причину появления индукционных электрических полей вокруг движущегося заряда. В чем заключается разница между предлагаемым подходом и ранее существующим. Ранее мы говорили, что движущийся заряд генерирует векторный потенциал, а уже изменяющийся векторный потенциал генерирует электрическое поле. Соотношение (4.4) дает возможность исключить эту промежуточную операцию и перейти непосредственно от свойств движущегося заряда к индукционным полям. Покажем, что из соотношению (4.4) следует и введенный ранее феноменологическим путем векторный потенциал, а, следовательно, и магнитное поле. Поскольку связь между векторным потенциалом и электрическим полем определяется соотношением (1.3), то равенство (4.4) мы можем переписать
от этого участка электрическое поле, определяемое соотношением (4.4). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Мы получили закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Этот закон мы можем называть законом электро-электрической индукции, так как он, минуя поля посредники (магнитное поле или векторный потенциал), дает прямой ответ на то, какие электрические поля генерирует вокруг себя движущийся электрический заряд. Данный закон дает также ответ о месте приложения сил взаимодействия между зарядами. Именно это соотношение, а не закон Фарадея, мы должны считать основным законом индукции, т.к. именно оно устанавливает причину появления индукционных электрических полей вокруг движущегося заряда. В чем заключается разница между предлагаемым подходом и ранее существующим. Ранее мы говорили, что движущийся заряд генерирует векторный потенциал, а уже изменяющийся векторный потенциал генерирует электрическое поле. Соотношение (4.4) дает возможность исключить эту промежуточную операцию и перейти непосредственно от свойств движущегося заряда к индукционным полям. Покажем, что из соотношению (4.4) следует и введенный ранее феноменологическим путем векторный потенциал, а, следовательно, и магнитное поле. Поскольку связь между векторным потенциалом и электрическим полем определяется соотношением (1.3), то равенство (4.4) мы можем переписать
откуда, интегрируя по времени, получаем
Это соотношение полностью соответствует определению векторного потенциала. Теперь мы видим, что векторный потенциал есть прямое следствие зависимости скалярного потенциала от относительной скорости заряда. Введение и векторного потенциала и магнитного поля это полезный математический приём, который позволяет упростить решение ряда электродинамических задач, однако, мы должны помнить, что первоосновой введение этих полей является скалярно-векторный потенциал.
Ранее мы ввели два симметричных закона: закон магнитоэлектрической и электромагнитной индукции. Мы указывали на то, что эти законы являются симметричными и, дополняя друг друга, позволяют решать вопросы распространения радиоволн. Вновь введенный закон электро-электрической индукции по сути дела объединяет эти два закона в один и исключает необходимость применения двух законов. Скалярно-векторный потенциал получен как обобщение законов электромагнитной и магнитоэлектрической индукции. Из этих же законов следуют и уравнения Максвелла, которые описывают волновые процессы в материальных средах. Из уравнений Максвелла следует конечность скорости распространения полей, которая равна скорости света.
Поскольку любой процесс распространения электрических полей и потенциалов всегда связан с запаздыванием, введём запаздывающий скалярно-векторный потенциал, считая, что поле этого потенциала распространяется в данной среде со скоростью света:
(4.5)
где  – составляющая скорости заряда
– составляющая скорости заряда ![]() , нормальная к вектору
, нормальная к вектору ![]() в момент времени
в момент времени  ,
, ![]() – расстояния между зарядом и точкой, в которой определяется поле, в момент времени
– расстояния между зарядом и точкой, в которой определяется поле, в момент времени ![]() .
.
Но возникает вопрос, на каких основаниях, если не использовать уравнения Максвелла, из которого следует волновое уравнение, вводится запаздывающий скалярно-векторный потенциал? Этот вопрос рассматривался в тринадцатом параграфе, когда определялась скорость распространения фронта волны напряжённости магнитного и электрического поля в длинной линии. Там, не прибегая к уравнениям Максвелла, было показано, что электрическое и магнитное поле распространяются с конечной скоростью, которая в вакуумной линии равна скорости света. Следовательно, такие поля запаздывают на время ![]() . Такое же запаздывание вводим в данном случае и для скалярно-векторного потенциала, который является носителем электрических полей.
. Такое же запаздывание вводим в данном случае и для скалярно-векторного потенциала, который является носителем электрических полей.
Используя соотношение ![]() , найдём поле в точке 1 (рис. 9).
, найдём поле в точке 1 (рис. 9).
Градиент числового значения радиуса вектора ![]() есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси
есть скалярная функция двух точек: начальной точки радиуса вектора и его конечной точки (в данном случае это точка 1 на оси ![]() и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая: 1) точка истока фиксирована и
и точка 0 в начале координат). Точка 1 является точкой истока, а точка 0 - точкой наблюдения. При определении градиента от функции, содержащей радиус в зависимости от условий задачи необходимо различать два случая: 1) точка истока фиксирована и ![]() рассматривается как функция положения точки наблюдения; и 2) точка наблюдения фиксирована и
рассматривается как функция положения точки наблюдения; и 2) точка наблюдения фиксирована и ![]() рассматривается как функция положения точки истока.
рассматривается как функция положения точки истока.
Будем считать, что заряд ![]() совершает колебательное движение вдоль оси
совершает колебательное движение вдоль оси ![]() , в окрестности точки 0, которая является точкой наблюдения, а точкой истока является фиксированная точка 1 и
, в окрестности точки 0, которая является точкой наблюдения, а точкой истока является фиксированная точка 1 и ![]() рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
рассматривается как функция положения заряда. Тогда значение электрического поля в точке 1 запишем:
При условии, что амплитуда колебаний заряда значительно меньше, чем расстояние до точки наблюдения, можно считать радиус вектор постоянная величина. При этом условии получаем:
(4.6)
где ![]() - какая-то фиксированная точка на оси
- какая-то фиксированная точка на оси ![]() .
.
Рис. 9. Схема формирования индуцированного электрического поля.
из (4.6) получаем:
(4.7)
Это и есть полный закон излучения движущегося заряда.
Если взять только первый член разложения 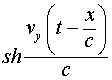 , то из (4.7) получим
, то из (4.7) получим
(4.8)
где  - запаздывающее ускорение заряда.
- запаздывающее ускорение заряда.
Это соотношение является волновым уравнением и определяет как амплитудные, так и фазовые характеристики волны электрического поля, излучаемого движущимся зарядом.
Если в качестве направления излучения взять вектор, лежащий в плоскости ![]() , и составляющий с осью
, и составляющий с осью ![]() угол
угол ![]() , то соотношение (4.8) принимает вид:
, то соотношение (4.8) принимает вид:
(4.9)
Соотношение (4.9) определяет диаграмму направленности излучения. Поскольку в данном случае есть осевая симметрия относительно оси ![]() , то можно вычислить полную диаграмму направленности рассмотренного излучателя. Эта диаграмма соответствует диаграмме направленности дипольного излучателя.
, то можно вычислить полную диаграмму направленности рассмотренного излучателя. Эта диаграмма соответствует диаграмме направленности дипольного излучателя.
Поскольку  - запаздывающий векторный потенциал, то соотношение (4.9) можно переписать
- запаздывающий векторный потенциал, то соотношение (4.9) можно переписать
Опять получено полное совпадение с уравнениями запаздывающего векторного потенциала в классической электродинамики, но векторный потенциал введён здесь не эвристическим феноменологическим способом, а с использованием понятия запаздывающего скалярно-векторного потенциала. Нужно отметить одно важное обстоятельство: в уравнениях Максвелла электрические поля, представляющие волну, вихревые. В данном же случае электрические поля носят градиентный характер.
Продемонстрируем ещё одну возможность, которую открывает соотношение (4.9). Известно, что в электродинамике существует такое понятие, как электрический диполь и дипольное излучение, когда заряды, колеблющиеся в электрическом диполе, излучают электромагнитные волны. Два заряда с противоположными знаками имеют дипольный момент:
(4.10)
где вектор ![]() направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
направлен от отрицательного заряда к положительному. Поэтому ток может быть выражен, через производную дипольного момента по времени
Следовательно
и
Подставляя данное соотношение в выражение (4.9), получаем закон излучения колеблющегося диполя.
(4.11)
Это также очень хорошо известное соотношение [1].
Таким образом, в процессе колебания электрического диполя создаются электрические поля двух видов. Во-первых, это электрические индукционные поля излучения, представляемые соотношениями (4.8), (4.9) и (4.10), связанные с ускорением заряда. С другой стороны, вокруг колеблющегося диполя образуются электрические поля статического диполя, которые изменяются во времени в связи с тем, что расстояние между зарядами зависит от времени. Суммарное же значение поля, вокруг такого диполя определяют как суперпозицию полученных полей.
Законы (4.8), (4.9), (4.11) - это законы прямого действия, в которых уже нет ни магнитных полей, ни векторных потенциалов. Т.е. те строительные леса, которыми являлись магнитное поле и магнитный векторный потенциал уже сняты и они нам больше не нужны.
Используя соотношение (4.9) можно получить законы отражения и рассеивания как для одиночных зарядов, так и, для любого их количества. Если какой-либо заряд или группа зарядов подвергаются действию внешнего (стороннего) электрического поля, то такие заряды начинают осуществлять вынужденное движение, и каждый из них излучает электрические поля в соответствии с соотношением (4.9). Суперпозиция электрических полей, излучаемых всеми зарядами, является электрической волной.
Если на заряд действует стороннее электрическое поле ![]() , то ускорение заряда определяют как:
, то ускорение заряда определяют как:
С учётом этого соотношение (21.11) принимает вид
(4.12)
где коэффициент  может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
может быть назван коэффициентом рассеивания (переизлучения) одиночного заряда в заданном направлении, поскольку он определяет способность заряда переизлучать действующее на него внешнее электрическое поле.
Волне электрического поля (4.9) сопутствует волна тока смещения:
Если заряд осуществляет своё движение под воздействием стороннего электрического поля ![]() , то ток смещения в дальней зоне записывают:
, то ток смещения в дальней зоне записывают:
(4.13)
Суммарная волна, которая представляет распространение электрических полей (4.12) и токов смещения (4.13), может быть названа электротоковой. В этой волне ток смещения отстаёт от волны электрического поля на ![]() .
.
Параллельно с электрическими волнами можно ввести магнитные волны, если положить, что
(4.14)
Введённое таким образом магнитное поле является вихревым. Сравнивая (4.13) и (4.14) получаем:
Интегрируя это соотношение по координате, находим значение магнитного поля
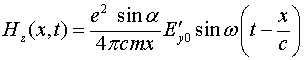
(4.15)
Таким образом, соотношения (4.12), (4.13) и (4.15) могут быть названы законами электро-электрической индукции, т.к. дают непосредственную связь между прикладываемыми к заряду сторонними электрическими полями и полями индуцируемыми этим зарядом в его окрестности. Сам же заряд выступает в данном случае в роли своеобразного трансформатора, обеспечивающего такое преизлучение.
Магнитное поле, которое можно вычислить при помощи соотношения (4.15), направлено нормально и к электрическому полю и к направлению распространения, а их отношение в каждой точке пространства составляет:
где ![]() - волновое сопротивление свободного пространства.
- волновое сопротивление свободного пространства.
Волновое сопротивление определяет активную мощность потерь на единичной площадке, расположенной нормально к направлению распространения волны:
Поэтому электротоковая волна, пересекая такую площадку, переносит через неё мощность, определяемую данным соотношением, что находится в согласии с теоремой Пойнтинга о потоке мощности электромагнитной волны. Поэтому, для нахождения всех параметров, характеризующих волновой процесс, распространения и переноса энергии посредством полей, достаточно рассмотрения лишь электротоковой волны и знания волнового сопротивления пространства. При этом совсем не обязательно вводить такое понятие, как «магнитное поле» и его векторный потенциал, хотя ничего незаконного в этом нет. В такой постановке соотношения, полученные для электрического и магнитного поля, полностью удовлетворяют теореме Гельмгольца. Эта теорема гласит, что всякое однозначное и непрерывное векторное поле ![]() , обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции
, обращающееся в ноль в бесконечности, может быть представлено, и притом единственным образом, в виде суммы градиента некоторой скалярной функции ![]() и ротора некоторой векторной функции
и ротора некоторой векторной функции ![]() , дивергенция которой равна нулю:
, дивергенция которой равна нулю:
Следовательно, должно существовать чёткое разделение полей на градиентные и вихревые. Видно, что в полученных выражениях для индуцируемых полей такое разделение имеется. Электрические поля носят градиентный характер, а магнитные – вихревой.
Таким образом, построение электродинамики нужно было начинать с признания зависимости скалярного потенциала от скорости, как это предлагал Вебер. Но в том-то и дело, что природа очень глубоко прячет свои секреты, и, чтобы прийти к такому простому выводу, пришлось пройти путь длиной почти в два столетия. Металлические опилки, которые так дружно выстраивались вокруг полюсов магнита, прямым образом указывали на наличие каких-то силовых полей потенциального характера, но на это не обратили внимания, поэтому и оказалось, что все разглядели только верхушку айсберга, значительная часть которого оставалась невидимой почти двести лет.
С учётом всего сказанного следует полагать, что в основе подавляющего большинства статических и динамических явлений в электродинамике лежит одна единственная формула (4.5), предполагающая зависимость скалярного потенциала заряда от скорости его движения. Из неё следует и статическое взаимодействие зарядов, и законы силового взаимодействия в случае их взаимного движения, и законы излучения и рассеивания. Такой подход позволил объяснить с позиций классической электродинамики следующие явления: фазовая аберрация и поперечный эффект Доплера, которые в рамках существующей классической электродинамики объяснения не находили. После всего сказанного можно снять строительные леса, такие как магнитное поле и магнитный векторный потенциал, которые не позволяют вот уже почти двести лет увидеть здание электродинамики во всём его величии и красоте.
Заметим, однако, что одно из основных уравнений индукции (4.8) можно было получить прямо из закона Ампера, ещё задолго до того, как появились уравнения Максвелла. Закон Ампера, выраженный в векторной форме, определяет магнитное поле в точке ![]() в следующем виде:
в следующем виде:
где ![]() - ток в элементе
- ток в элементе ![]() ,
, ![]() - вектор, направленный из
- вектор, направленный из ![]() в точку
в точку ![]() .
.
Можно показать, что
и, кроме того, что
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
Где
(4.16)
Замечательным свойством этого выражения является то, что векторный потенциал зависит от расстояния до точки наблюдения как ![]() . Именно это свойство и позволяет получить законы излучения.
. Именно это свойство и позволяет получить законы излучения.
Поскольку ![]() , где
, где ![]() количество зарядов, приходящееся на единицу длины проводника, из (4.16) получаем:
количество зарядов, приходящееся на единицу длины проводника, из (4.16) получаем:
Для одиночного заряда ![]() это соотношение принимает вид:
это соотношение принимает вид:
а поскольку
то
(4.17)
Для одиночного заряда это соотношение выглядит следующим образом:
(4.18)
Если в соотношениях (4.17) и (4.18) учесть, что потенциалы распространяются с конечной скоростью и учесть запаздывание  , и с учётом, что для вакуума
, и с учётом, что для вакуума  , эти соотношения примут вид:
, эти соотношения примут вид:
(4.19)
(4.20)
Соотношения (4.19) и (4.20) представляют, как показано выше (см. (4.8)), волновые уравнения. Отметим, что эти уравнения - это решение уравнений Максвелла, но в данном случае они получены непосредственно из закона Ампера, вообще не прибегая к уравнениям Максвелла. Остаётся только задать вопрос, почему электродинамика в своё время не пошла этим путём?
Литература
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.
- Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967, - 664 - с.
- Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с.
- Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5
- Mende F. F. On refinement of certain laws of classical electrodynamics, arXiv, physics/0402084.
- Менде Ф. Ф. К вопросу об уточнении уравнений элетромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.