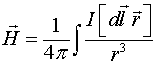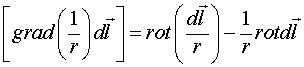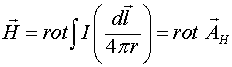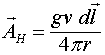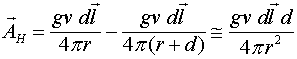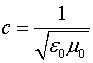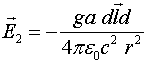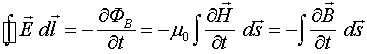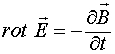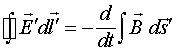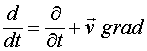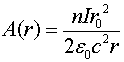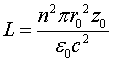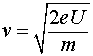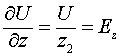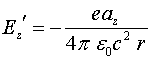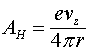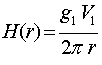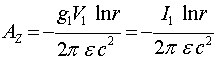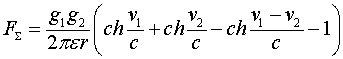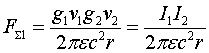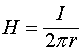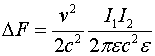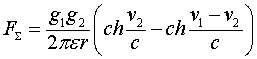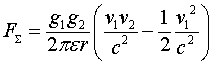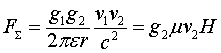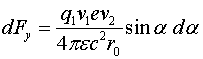Векторный потенциал магнитного поля и природа его возникновения
| Федор Федорович Менде | |
| Дата рождения: |
02.07.1939 г. |
|---|---|
| Гражданство: | |
| Учёная степень: | |
| Сайт: |
http://fmnauka.narod.ru/ http://bolshoyforum.org/forum/index.php?board=50.0 |
Содержание
Векторный потенциал магнитного поля в классической электродинамике
Длительное время считалось, что векторный потенциал магнитного поля есть некоторое математическое понятие, не имеющее какого-либо физического смысла. Уже позже начали понимать, что производная этого потенциала по времени определяет электрическое поле, а также то, что от этого потенциала зависит силовое взаимодействие токонесущих систем.
Магнитное поле в своё время было введено Ампером феноменологическим путём на основе наблюдения силового взаимодействия между проводниками, по которым течёт ток. Закон Ампера, выраженный в векторной форме, определяет магнитное поле в точке наблюдения в следующем виде:
где ![]() - ток в элементе
- ток в элементе ![]() ,
, ![]() - вектор, направленный из
- вектор, направленный из ![]() в точку наблюдения (рис. 1).
в точку наблюдения (рис. 1).
Можно показать, что
и, кроме того, что
Рис. 1. Формирование векторного потенциала элементом проводника ![]() , по которому течёт ток
, по которому течёт ток ![]() .
.
Но ротор ![]() равен нулю и поэтому окончательно
равен нулю и поэтому окончательно
где
(1.1)
векторный потенциал магнитного поля.
Замечательным свойством этого выражения является то, что зависимость векторного потенциал обратно пропорциональна расстоянию до точки наблюдения, что характерно для законов излучения.
Поскольку ![]() , где
, где ![]() количество зарядов, приходящееся на единицу длины проводника, из (1.1) получаем:
количество зарядов, приходящееся на единицу длины проводника, из (1.1) получаем:
Если размер элемента ![]() , по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом
, по которому течёт ток, значительно меньше, чем расстояние до точки наблюдения, то векторный потенциал, порождаемый элементом ![]() , по которому течёт ток
, по которому течёт ток ![]() имеет вид
имеет вид
(1.2)
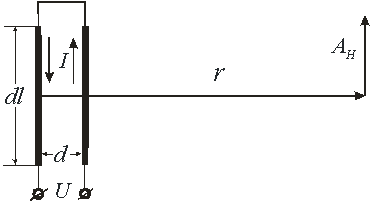
Из этого соотношения следует интересный факт. Даже на постоянном токе зависимость векторного потенциала от расстояния соответствует законам излучения. И, казалось бы, что, меняя скачками ток в коротком отрезке провода, и измеряя векторный потенциал в удалённой точке, можно передавать информацию в эту точку по законам излучения. Но этому мешает то обстоятельство, что цепь постоянного тока всегда замкнута на локальный источник питания и поэтому всегда есть как прямой, так и обратный провод. Эта особенность приводит к тому, что скалярный потенциал в дальней зоне оказывается обратно пропорционален квадрату расстояния до наблюдаемой точки. Это легко показать на примере двух параллельных элементов проводника, расположенных на расстоянии ![]() (рис. 2), в которых текут встречные токи.
(рис. 2), в которых текут встречные токи.
В этом случае векторный потенциал в удалённой зоне определяется как сумма векторных потенциалов, создаваемых в дальней зоне каждым токовым элементом в отдельности.
Рис. 2. Формирование векторного потенциала двумя параллельными участками проводников, по которым текут встречные токи.
(1.3)
Поскольку
(1.4)
где ![]() - магнитная проницаемость вакуума, из (1.2) и (1.3) получаем:
- магнитная проницаемость вакуума, из (1.2) и (1.3) получаем:
(1.5)
(1.6)
Из уравнений Максвелла известно, что электрические поля распространяются в свободном пространстве со скоростью
где ![]() - диэлектрическая проницаемость вакуума. Если учесть это соотношение, то равенства (1.5) и (1.6) можно переписать:
- диэлектрическая проницаемость вакуума. Если учесть это соотношение, то равенства (1.5) и (1.6) можно переписать:
Если имеется точечный заряд ![]() , то эти соотношения принимают вид:
, то эти соотношения принимают вид:
Основная задача законов индукции заключается в выяснении причин появления в пространстве электрических полей, а, следовательно, и сил действующих на заряд, в данной точке пространства, в данной ИСО. Это главная задача индукции, т.к. только электрические поля, генерируемые тем или иным способом, оказывают силовые воздействия на заряд. Такие поля могут возникать при изменении расположения других зарядов вокруг заданной точки пространства. Если вокруг рассматриваемой точки имеется какая-то статическая конфигурация зарядов, то напряженность электрического поля в этой точке будет определяться соотношением ![]() , где
, где ![]() скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций. Если изменить расположение зарядов, то этой новой конфигурации будут соответствовать и другие значения скалярного потенциала, а, следовательно, и другие значения напряженности электрического поля. Но такое перемещение зарядов в пространстве в обязательном порядке сопряжено с их ускорением и последующим замедлением. Ускорение или замедление зарядов как показано выше также приводит к возникновению в окружающем пространстве электрических полей индукции.
скалярный потенциал, определяемый данной конфигурацией по принципу суперпозиций. Если изменить расположение зарядов, то этой новой конфигурации будут соответствовать и другие значения скалярного потенциала, а, следовательно, и другие значения напряженности электрического поля. Но такое перемещение зарядов в пространстве в обязательном порядке сопряжено с их ускорением и последующим замедлением. Ускорение или замедление зарядов как показано выше также приводит к возникновению в окружающем пространстве электрических полей индукции.
Основным законом индукции в классической электродинамике является закон Фарадея, который для вакуума записывается следующим образом:
(1.7)
где ![]() - вектор магнитной индукции,
- вектор магнитной индукции, ![]() - поток магнитной индукции.
- поток магнитной индукции.
Из этого закона следует, что циркуляция вектора электрического поля равна изменению потока магнитной индукции через площадку, которую охватывает данный контур. Сразу подчеркнём то обстоятельство, что рассматриваемый закон представляет процессы взаимной индукции, т.к. для получения циркуляции вектора ![]() берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.7) получают первое уравнение Максвелла
берётся стороннее магнитное поле, сформированное сторонним источником. Этот закон является интегральным и не даёт локальной связи между магнитным и электрическим полем. Из соотношения (1.7) получают первое уравнение Максвелла
(1.8)
Сразу укажем на терминологическую ошибку. Закон Фарадея следует называть не законом электромагнитной индукции, как это делается сейчас в существующей литературе, а законом магнитоэлектрической индукции, т.к. изменение магнитных полей приводит к возникновению электрических полей, а не наоборот.
Но здесь необходимо сделать одно замечание. Переход от интегральной формы (1.7) к дифференциальной форме (1.8) не вполне законен. Правомерность такого перехода справедлива только в том случае, когда контур интегрирования в левой части соотношения (1.7) охватывает площадь интегрирования в интеграле правой части. Но опыты, которые провел Фарадей, совсем не предполагают этого, контур интегрирования в левой части, а вернее проволока, в которой индуцировалась э.д.с., может не совпадать с границами площадки интегрирования в правой части. Главным условием соблюдения соотношения (1.7) являлось то, что контур интегрирования в правой части должен охватывать контур интегрирования в левой. Примером тому может служить случай длинного соленоида, когда поток индукции сосредоточен во внутренней его части, а контур интегрирования может проходить за его пределами, где магнитных полей нет. Важно только, чтобы контур интегрирования в левой части соотношения (1.7) охватывал соленоид.
Введём векторный потенциал ![]() , удовлетворяющий равенству
, удовлетворяющий равенству ![]() , где контур интегрирования совпадает с контуром интегрирования в соотношении (1.6), а вектор
, где контур интегрирования совпадает с контуром интегрирования в соотношении (1.6), а вектор ![]() определен на всех его участках, тогда
определен на всех его участках, тогда
(1.9)
Это соотношение ранее уже использовалось (см. (1.4)).
Путём введения вектор ![]() обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора
обеспечивается локальную связь между этим вектором и электрическим полем, а также между пространственными производными этого вектора и магнитным полем. Следовательно, зная производные вектора ![]() по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор
по времени и по координатам, можно определить индуцируемые электрические и магнитные поля. Введенный таким образом вектор ![]() , связан с магнитным полем соотношением:
, связан с магнитным полем соотношением:
(1.10)
Таким образом, вектор ![]() является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
является более универсальным понятием, чем вектор магнитного поля, поскольку даёт возможность определять как магнитные, так и электрические поля.
До сих пор решение вопроса о возникновении электрических полей в движущихся системах можно было осуществлять двумя путями. Первый - заключался в вычислении силы Лоренца, действующей на движущиеся заряды, второй путь заключался в измерении изменения магнитного потока через исследуемый контур. Оба метода давали одинаковый результат. Это было непонятно. В связи с непониманием физической природы такого положения дел и начали считать, что униполярный генератор является исключением из правила потока [1]. Рассмотрим эту ситуацию подробнее.
Для того чтобы ответить на поставленный вопрос, следует несколько изменить соотношение (1.9), заменив в нём частную производную на полную:
(1.11)
Штрих около вектора ![]() означает, что это поле определяется в движущейся системе координат, в то время как вектор
означает, что это поле определяется в движущейся системе координат, в то время как вектор ![]() определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.11) можно переписать следующим образом:
определен в неподвижной системе. Таким образом, предполагается, что векторный потенциал может иметь, как локальную, так и конвекционную производную, т.е. может меняться, как за счет изменения локального времени, так и за счет движения в пространственно меняющемся поле этого потенциала. Соотношение (1.11) можно переписать следующим образом:
где ![]() - скорость штрихованной системы.
- скорость штрихованной системы.
Следовательно, дополнительная сила, действующая на заряд в движущейся системе, запишется
Эта сила зависит только от пространственных производных векторного потенциала и скорости штрихованной системы.
Заряд, движущийся в поле векторного потенциала ![]() со скоростью
со скоростью ![]() , обладает также потенциальной энергией [1]
, обладает также потенциальной энергией [1]
Поэтому должна существовать еще одна сила, действующая на заряд в движущейся ИСО, а именно:
Таким образом, величина ![]() играет такую же роль, что и скалярный потенциал
играет такую же роль, что и скалярный потенциал ![]() , градиент которого дает электрическое поле. Следовательно, суммарная сила, которая действует на заряд, движущийся в поле векторного потенциала, может иметь три составляющие и запишется как
, градиент которого дает электрическое поле. Следовательно, суммарная сила, которая действует на заряд, движущийся в поле векторного потенциала, может иметь три составляющие и запишется как
(1.12)
Первая из составляющих этой силы действует на неподвижный заряд, когда векторный потенциал имеет локальную производную по времени. Вторая составляющая также определяет изменения векторного потенциала во времени, но они связаны уже с движением заряда в пространственно меняющемся поле этого потенциала. Совсем иная природа у силы, которая определяется последним слагаемым соотношения (1.12). Она связана с тем, что заряд, двигающийся в поле векторного потенциала, обладает потенциальной энергией, градиент которой и дает силу. Из соотношения (1.12) следует
(1.13)
Это и есть полный закон взаимной индукции. Он определяет все электрические поля, которые могут возникать в заданной точке пространства, причем эта точка может быть как неподвижной, так и движущейся. Этот единый закон включает в себя и закон Фарадея, и ту часть силы Лоренца, которая связана с движением заряда в магнитном поле. Этот закон без всяких исключений дает ответ на все вопросы, касающиеся взаимной магнитоэлектрической индукции. Показательно, что, если взять ротор от обеих частей равенства (1.13), пытаясь получить первое уравнение Максвелла, то сразу будет потеряна существенная часть информации, т.к. ротор от градиента тождественно равен нулю.
Если выделить те силы, которые связаны с движением заряда в поле векторного потенциала, и учесть, что
то из (1.12) получим
(1.14)
Учитывая (1.10), запишем:
(1.15)
или
(1.16)
Окончательно:
(1.17)
Может показаться, что соотношение (11.17) представляет силу Лоренца, однако, это не так. В этом соотношении и поле ![]() , и поле
, и поле ![]() являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.17) добавить слагаемое
являются индуцированными, первое связано с локальной производной векторного потенциала по времени, второе же обязано движению заряда в пространственно меняющемся поле этого потенциала. Чтобы получить полную силу, действующую на заряд, необходимо для случая, когда система не является электронейтральной, к правой части соотношения (1.17) добавить слагаемое ![]() :
:
где ![]() - скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
- скалярный потенциал, создаваемый в точке наблюдения нескомпенсированными зарядами.
Теперь соотношение (1.13) можно переписать следующим образом:
(1.18)
или, собрав первые два члена в полную производную векторного потенциала по времени, и, внеся под знак градиента два последних члена правой части соотношения (1.18), получим:
(1.19)
Если обе части соотношения (1.19) умножить на величину заряда, то можно получить полную силу, действующую на заряд. От силы Лоренца она будет отличаться силой  . Из соотношения (15.13) видно, что величина
. Из соотношения (15.13) видно, что величина ![]() играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (1.19) и учесть, что
играет роль обобщенного скалярного потенциала. Если взять ротор от обеих частей соотношения (1.19) и учесть, что ![]() , то получим:
, то получим:
Если в данном соотношении заменить полную производную на частную, т.е. считать, что поля определяются только в заданной инерциальной системе, то получим первое уравнение Максвелла.
Ранее сила Лоренца рассматривалась как фундаментальный опытный факт, не связанный с законом индукции. Расчетным путем получить последнее слагаемое правой части соотношения (1.17) можно было только в рамках СТО. В данном случае все слагаемые соотношение (1.17) получены из закона индукции в рамках преобразований Галилея. Причем соотношение (1.17) это и есть полный закон взаимной индукции, если его записать в терминах векторного потенциала. Это есть как раз то правило, которое дает возможность, зная поля в одной ИСО, вычислять поля в другой инерциальной системе, и этого правила до сих пор не было в классической электродинамике.
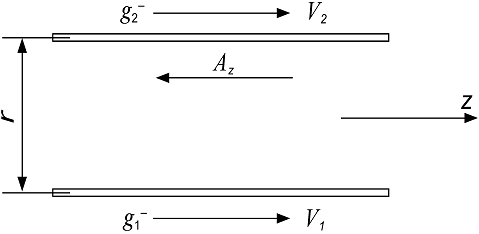
Структуру сил, действующих на движущийся заряд, легко понять на примере, когда заряд движется между двумя параллельными плоскостями, по которым протекает ток (рис. 3).
Выберем оси координат таким образом, чтобы ось ![]() была направлена нормально к плоскостям, а ось
была направлена нормально к плоскостям, а ось ![]() параллельна им. Тогда для случая, когда расстояние между пластинами значительно меньше их размеров (в данном случае на рисунке это соотношение не соблюдено), магнитное
параллельна им. Тогда для случая, когда расстояние между пластинами значительно меньше их размеров (в данном случае на рисунке это соотношение не соблюдено), магнитное
Рис. 3. Силы, действующие на заряд, движущийся в поле векторного потенциала.
поле ![]() между ними будет равно удельному току
между ними будет равно удельному току ![]() , протекающему по пластинам. Если положить, что векторный потенциал на нижней пластине равен нулю, то его
, протекающему по пластинам. Если положить, что векторный потенциал на нижней пластине равен нулю, то его ![]() – компонента, отсчитываемая от нижней пластины, будет возрастать по закону
– компонента, отсчитываемая от нижней пластины, будет возрастать по закону ![]() .
.
Если электрон двигается в направлении оси ![]() вблизи нижней пластины со скоростью
вблизи нижней пластины со скоростью ![]() , то сила
, то сила ![]() , действующая на заряд, определяется последним слагаемым соотношения (1.12) и равна
, действующая на заряд, определяется последним слагаемым соотношения (1.12) и равна
(1.20)
Направлена эта сила от нижней пластины к верхней.
Если заряд двигается вдоль оси ![]() от нижней пластины к верхней со скоростью
от нижней пластины к верхней со скоростью ![]() , то для нахождения силы следует использовать уже второе слагаемое правой части соотношения (1.12). Эта сила по абсолютной величине опять равна силе, определяемой соотношением (1.20), и направлена в сторону противоположную оси
, то для нахождения силы следует использовать уже второе слагаемое правой части соотношения (1.12). Эта сила по абсолютной величине опять равна силе, определяемой соотношением (1.20), и направлена в сторону противоположную оси ![]() . При любых других направлениях движения суммарная сила будет векторной суммой двух сил, представляемых последними слагаемыми соотношения (1.12). Суммарная же величина этой силы по-прежнему будет определяться соотношением (1.17), а сама сила всегда будет нормальной к направлению движения заряда. Ранее наличие такой силы рассматривалось как действие силы Лоренца, природа которой была неизвестна и вводилась как некая экспериментальная аксиома. Теперь понятно, что она является следствием совместного действия двух сил, различных по своей природе, физический смысл которых теперь определён. Однако в данном случае возникает один существенный вопрос. С точки зрения третьего закона Ньютона, если на заряд действует сила, то должна быть и равнодействующая ей сила и место приложение такой силы должно быть известно. Концепция магнитного поля ответа на этот вопрос не даёт, поскольку и магнитное поле, и векторный потенциал выступают в качестве самостоятельной субстанции, с которой и происходит такое взаимодействие.
. При любых других направлениях движения суммарная сила будет векторной суммой двух сил, представляемых последними слагаемыми соотношения (1.12). Суммарная же величина этой силы по-прежнему будет определяться соотношением (1.17), а сама сила всегда будет нормальной к направлению движения заряда. Ранее наличие такой силы рассматривалось как действие силы Лоренца, природа которой была неизвестна и вводилась как некая экспериментальная аксиома. Теперь понятно, что она является следствием совместного действия двух сил, различных по своей природе, физический смысл которых теперь определён. Однако в данном случае возникает один существенный вопрос. С точки зрения третьего закона Ньютона, если на заряд действует сила, то должна быть и равнодействующая ей сила и место приложение такой силы должно быть известно. Концепция магнитного поля ответа на этот вопрос не даёт, поскольку и магнитное поле, и векторный потенциал выступают в качестве самостоятельной субстанции, с которой и происходит такое взаимодействие.
Понимание структуры сил дает возможность посмотреть на уже известные явления с другой точки зрения. Например, с чем связано существование сил, которые растягивают петлю с током? В данном случае это обстоятельство может интерпретироваться не как действие силы Лоренца, а с энергетической точки зрения. Ток, текущий по элементу кольцевого витка находится в поле векторного потенциала, создаваемого остальными элементами этого витка, а, следовательно, имеет запас потенциальной энергии. Сила, действующая на такой элемент, обусловлена наличием у него градиента потенциальной энергии, и пропорциональна градиенту скалярного произведения величины тока на векторный потенциал в данной точке. Таким образом, можно объяснить и происхождение пондеромоторных сил. Если ток разбить на отдельные токовые нити, то все они будут по отдельности создавать поле векторного потенциала. Суммарное поле будет действовать на каждую нить в отдельности, и в соответствии с последним слагаемым правой части соотношения (1.12) это будет приводить к взаимному их притяжению.
Следует подчеркнуть, что в соотношении (1.14) и (1.19) все поля имеют индукционное происхождение, и они связаны то ли с локальной производной векторного потенциала, то ли с движением заряда в пространственно меняющемся поле этого потенциала. Если поля во времени не изменяются, то в правой части соотношений (1.14) и (1.15) остаются только последние слагаемые, и они объясняют работу всех существующих электрогенераторов с движущимися механическими частями, в том числе и работу униполярного генератора. Соотношение (1.13) дает возможность физически объяснить все составляющие напряженности электрического поля, возникающего в неподвижной и движущейся ИСО. В случае униполярного генератора в формировании силы, действующей на заряд, принимают участие два последних слагаемых правой части равенства (1.13), внося одинаковые вклады. Теперь ясно, что представление закона индукции в терминах векторного потенциала это и есть тот „основополагающий принцип”, об отсутствии котрого говорится в работе [1].
При рассмотрении действия магнитного поля на движущийся заряд уже отмечалась его посредническая роль и отсутствие закона прямого действия между движущимися зарядами. Введения векторного потенциала также не дает ответа на этот вопрос, этот потенциал по-прежнему играет посредническую роль и не отвечает на вопрос о конкретном месте приложения сил.
Тепер покажем, что соотношения, полученные путем феноменологического введения магнитного векторного потенциала, могут быть получены и непосредственно из закона Фарадея. Сам Фарадей при проведении своих опытов установил, что в контуре индуцируется ток, когда в соседнем контуре включается или выключается постоянный ток, или соседний контур с постоянным током движется относительно первого контура. Поэтому в общем виде закон Фарадея следует записать следующим образом:
(1.21)
Данная запись закона указывает на то, что при записи циркуляции вектора ![]() в движущейся (штрихованной) системе координат, около
в движущейся (штрихованной) системе координат, около ![]() и
и ![]() следует ставить штрихи, указывающие на тот, что поток определён в одной ИСО, а поля в другой. Если же циркуляция определяется только в заданной ИСО, то штрихи около
следует ставить штрихи, указывающие на тот, что поток определён в одной ИСО, а поля в другой. Если же циркуляция определяется только в заданной ИСО, то штрихи около ![]() и
и ![]() отсутствуют, но при этом справа в выражении (1.21) должна стоять частная производная по времени.
отсутствуют, но при этом справа в выражении (1.21) должна стоять частная производная по времени.
Полная производная по времени в соотношении (1.21) означает независимость конечного результата появления э.д.с. в контуре от способа изменения потока. Поток может изменяться как за счет локальной производной магнитного потока по времени, так и за счет того, что ИСО, в которой измеряется циркуляция ![]() , движется в пространственно меняющемся поле
, движется в пространственно меняющемся поле ![]() . Величину магнитного потока в соотношении (1.21) вычисляем при помощи выражения:
. Величину магнитного потока в соотношении (1.21) вычисляем при помощи выражения:
(1.22)
где магнитная индукция ![]() определена в неподвижной системе координат, а элемент
определена в неподвижной системе координат, а элемент ![]() определен в движущейся системе.
определен в движущейся системе.
Учитывая (1.21), из (1.22) получаем:
(1.23)
В данном случае контурный интеграл берется по контуру ![]() , охватывающему площадку
, охватывающему площадку![]() . Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е.
. Сразу отметим, что все дальнейшее изложение будет вестись в предположении справедливости преобразований Галилея, т.е. ![]() и
и ![]() . Поскольку
. Поскольку![]() , из (1.23) получаем соотношение
, из (1.23) получаем соотношение
(1.24)
Из соотношения (1.24) следует, что при движении в магнитном поле возникает дополнительное электрическое поле, определяемое последним слагаемым этого соотношения. Заметим, что данное соотношение получено не путем введения силы Лоренца аксиоматическим способом или из ковариантных преобразований Лоренца, а непосредственно из закона Фарадея, причем в рамках преобразований Галилея. Таким образом, сила Лоренца является прямым следствием закона магнитоэлектрической индукции.
Учитывая, что![]() , из соотношение (1.23) получаем
, из соотношение (1.23) получаем
и далее
(1.25)
Снова получено соотношение (1.13), но получено оно непосредственно из закона Фарадея. Правда, и этот путь пока не проливает свет на физическую природу происхождения силы Лоренца, так как истинные физические причины возникновения и магнитного поля и векторного потенциала нам все равно пока не ясны.
Физические причины возникновения векторного потенциала магнитного поля
Тот путь, который продемонстрирован в предыдущем разделе, касающийся введения полных производных полей, пройден в значительной части ещё Герцем, о чём подробно написано в работе [2]. Правда, Герц не вводил понятие векторных потенциалов, а оперировал только полями, но это не умаляет его заслуг. Он ошибался лишь в том, что считал электрические и магнитные поля инвариантами скорости.
Поля, которые создаются в данной ИСО движущимися зарядами и движущимися источниками электромагнитных волн, будем называть динамическими. Примером динамического поля может служить магнитное поле, которое возникает вокруг движущихся зарядов.
В классической электродинамике отсутствуют правила преобразования электрических и магнитных полей при переходе из одной инерциальной системы в другую. Этот недостаток устраняет СТО, основой которой являются ковариантные преобразования Лоренца. При всей математической обоснованности такого подхода физическая сущность таких преобразований до настоящего времени остаётся невыясненной [3].
В данном разделе будет сделана попытка найти именно физически обоснованные пути получения преобразований полей при переходе из одной ИСО в другую, а также выяснить какие динамические потенциалы и поля могут генерировать движущиеся заряды. Первый шаг, продемонстрированный в работах [4-7], был сделан в этом направлении путём введения симметричных законов магнитоэлектрической и электромагнитной индукции. Эти законы записываются следующим образом:
(2.1)
или
(2.2)
Для постоянных полей эти соотношения имеют вид:
(2.3)
В соотношениях (2.1-2.3), предполагающих справедливость преобразований Галилея, штрихованные и не штрихованные величины представляют поля и элементы в движущейся и неподвижной ИСО соответственно. Следует заметить, что преобразования (2.3) ранее можно было получить только из преобразований Лоренца.
Соотношения (2.1–2.3), представляющие законы индукции, не дают информации о том, каким образом возникли поля в исходной неподвижной ИСО. Они описывают только закономерности распространения и преобразования полей в случае движения по отношению к уже существующим полям.
Соотношения (2.3) свидетельствуют о том, что в случае относительного движения систем отсчета, между полями ![]() и
и ![]() существует перекрестная связь, т.е. движение в полях
существует перекрестная связь, т.е. движение в полях ![]() приводит к появлению полей
приводит к появлению полей ![]() и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [4]. Электрическое поле
и наоборот. Из этих соотношений вытекают дополнительные следствия, которые впервые были рассмотрены в работе [4]. Электрическое поле  за пределами заряженного длинного стержня, на единицу длины которого приходится заряд
за пределами заряженного длинного стержня, на единицу длины которого приходится заряд ![]() , убывает по закону
, убывает по закону ![]() , где
, где ![]() - расстояние от центральной оси стержня до точки наблюдения.
- расстояние от центральной оси стержня до точки наблюдения.
Если параллельно оси стержня в поле ![]() начать двигать со скоростью
начать двигать со скоростью ![]() другую ИСО, то в ней появится дополнительное магнитное поле
другую ИСО, то в ней появится дополнительное магнитное поле ![]() . Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью
. Если теперь по отношению к уже движущейся ИСО начать двигать третью систему отсчета со скоростью ![]() , то уже за счет движения в поле
, то уже за счет движения в поле ![]() появится добавка к электрическому полю
появится добавка к электрическому полю ![]() . Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля
. Данный процесс можно продолжать и далее, в результате чего может быть получен ряд, дающий величину электрического поля ![]() в движущейся ИСО при достижении скорости
в движущейся ИСО при достижении скорости ![]() , когда
, когда ![]() , а
, а ![]() . В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
. В конечном итоге в движущейся ИСО величина динамического электрического поля окажется больше, чем в исходной и определиться соотношением:
Если речь идет об электрическом поле одиночного заряда , то его электрическое поле будет определяться соотношением:
где ![]() - нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
- нормальная составляющая скорости заряда к вектору, соединяющему движущийся заряд и точку наблюдения.
Выражение для скалярного потенциала, создаваемого движущимся зарядом, для этого случая запишется следующим образом:
(2.4)
где ![]() - скалярный потенциал неподвижного заряда. Потенциал
- скалярный потенциал неподвижного заряда. Потенциал ![]() может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
может быть назван скалярно-векторным, т.к. он зависит не только от абсолютной величины заряда, но и от скорости и направления его движения по отношению к точке наблюдения. Максимальное значение этот потенциал имеет в направлении нормальном к движению самого заряда. Более того, если скорость заряда меняется, что связано с его ускорением, то могут быть вычислены и электрические поля, индуцируемые ускоряемым зарядом.
Фарадей установил закон индукции, проводя эксперименты на соленоидах, включая и выключая в них ток, или двигая по отношению к соленоидам, через которые протекал постоянный ток, витки проволоки, к которым подключался гальванометр. Его точка зрения, которая считается верной и сегодня, сводилась к тому, что если к соленоиду подключён источник постоянного напряжения ![]() , то ток во всех его витках нарастает по линейному закону
, то ток во всех его витках нарастает по линейному закону
(2.5)
где ![]() - индуктивность соленоида.
- индуктивность соленоида.
Следовательно, магнитное поле при такой интерпретации на всём протяжении соленоида будет нарастать синхронно. Однако так ли это на самом деле? Для того чтобы разобраться в этом, рассмотрим вопрос о том, как будет нарастать ток в закороченном отрезке длинной линии.
Если линию (рис. 4) закоротить на расстоянии ![]() от ее начала, то суммарная индуктивность линии составит величину
от ее начала, то суммарная индуктивность линии составит величину 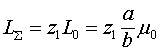 . Если волновое сопротивление линии составляет
. Если волновое сопротивление линии составляет ![]() и к ней подключить постоянного напряжения, в ней начнет распространяться волна тока
и к ней подключить постоянного напряжения, в ней начнет распространяться волна тока 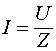 и напряжения
и напряжения ![]() , как показано на рис. 4 . Волна тока в правой своей части имеет переходной участок
, как показано на рис. 4 . Волна тока в правой своей части имеет переходной участок ![]() , который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса
, который именуется фронтом напряжения. Этот участок соответствует времени переходного процесса 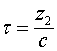 , за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
, за которое напряжение источника, подключаемого к линии, достигает на её вход своего номинального значения.
Рис. 4. Распространение волны тока и напряжения в длинной линии.
Именно на этом переходном участке и происходит ускорение зарядов от нулевой скорости в его начале, до значений необходимых для создания номинального тока в линии, величина которого определяется соотношением 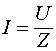 . К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Принято также, что время этого переходного процесса значительно меньше, чем время, за которое фронт напряжения пробегает по линии в одну сторону. Интервал
. К этому участку и приложено напряжение источника питания. В данном случае принято, что во время переходного процесса напряжение нарастает по линейному закону (хотя в общем случае оно может нарастать по любому другому закону). Принято также, что время этого переходного процесса значительно меньше, чем время, за которое фронт напряжения пробегает по линии в одну сторону. Интервал ![]() соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что
соответствует переходному процессу, который связан с инерционными свойствами устройства, подключающего источник напряжения к линии. Предполагается, что ![]() >>
>>![]() .
.
В момент, когда на перемычке, закорачивающей длинную линию, на которой выполняется граничное условие ![]() , появляется фронт напряжения
, появляется фронт напряжения ![]() , возникает отраженная волна с напряжением
, возникает отраженная волна с напряжением ![]() , бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен
, бегущая в обратном направлении. Так как ток в этой отраженной волне равен напряжению с отрицательным знаком и двигается она в обратном направлении, то суммарный ток, создаваемый этой волной будет равен  , т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный
, т.е. он будет течь в том же направлении, что и ток падающей волны. Таким образом, отраженная волна, двигаясь в обратном направлении, будет оставлять после себя ток, равный ![]() , и нулевое напряжение. Когда фронт напряжения возвратиться к началу линии, он принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию фронт напряжения
, и нулевое напряжение. Когда фронт напряжения возвратиться к началу линии, он принесет с собой состояние удвоенного начального тока и нулевое напряжение. Источник снова пошлет в линию фронт напряжения ![]() и ток
и ток ![]() . Этот ток сложится с током
. Этот ток сложится с током ![]() , и суммарный ток в линии составит
, и суммарный ток в линии составит ![]() . Ток и далее будет нарастать ступеньками, добавляя каждый очередной раз к своему прежнему значению величину
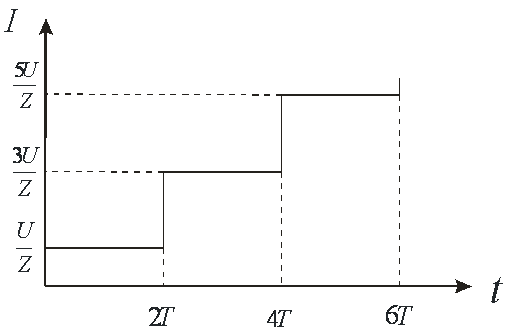
. Ток и далее будет нарастать ступеньками, добавляя каждый очередной раз к своему прежнему значению величину ![]() . Если этот процесс отобразить во времени, то он будет выглядеть, как показано на рис. 5. На этом рисунке время
. Если этот процесс отобразить во времени, то он будет выглядеть, как показано на рис. 5. На этом рисунке время  равно времени, за которое фронт напряжения пробегает по линии в одну сторону от её начала до закороченного участка.
равно времени, за которое фронт напряжения пробегает по линии в одну сторону от её начала до закороченного участка.
Особенностью такого процесса является то, что отбор энергии от источника напряжения не будет подчиняться линейному закону, а будет иметь скачкообразный характер. Мощность, отбираемая на интервале времени от нуля до ![]() , будет составлять
, будет составлять ![]() . Но на каждом последующем интервале времени, равном
. Но на каждом последующем интервале времени, равном ![]() , она будет возрастать уже на величину
, она будет возрастать уже на величину ![]() .
.
Таким образом, нарастание тока носит вовсе не линейный, а скачкообразный характер, и он тем более выражен, чем больше длина линии. Указанный процесс имеет место при любой длине линии. При малой длине линии скачки следуют через малые промежутки времени и зависимость тока от времени приближенно можно считать линейной, что и характерно для элементов с сосредоточенными параметрами.
Следует обратить внимание на то, что, мощность, отбираемая закороченной линией у источника напряжения (рис. 4), не является линейной функцией, а по истечении времени равному ![]() скачком увеличивается на
скачком увеличивается на ![]() , причем первый скачек соответствует отбираемой мощности
, причем первый скачек соответствует отбираемой мощности ![]() .
.
Рис. 5. График зависимости входного тока от времени для закороченной линии.
Нетрудно показать, что магнитный поток в данном случае изменяется по линейному закону (рис. 6). Действительно, во время прямого хода, до момента достижения волной закороченного участка, поток будет увеличиваться по линейному закону, и к моменту ![]() достигнет величины
достигнет величины  .
.
Когда, отразившись от закороченного участка, фронт напряжения начнет двигаться в обратном направлении, то поток будет продолжать возрастать по линейному закону, и к моменту прихода фронта напряжения обратно к источнику напряжения достигнет величины 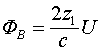 . Таким образом, при подключении закороченной линии к источнику напряжения выполняется закон индукции
. Таким образом, при подключении закороченной линии к источнику напряжения выполняется закон индукции 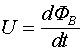 .
.
Рис. 6. Зависимость магнитного потока от времени для закороченной линии.
Электрический поток в линии тоже будет изменяться, но по другому закону (рис. 7).
Рис. 7. Зависимость электрического потока от времени для закороченной линии.
В отличие от магнитного потока он будет изменяться периодически, то, возрастая, то, убывая, по линейному закону. Когда волна движется в положительном направлении, одновременно возрастает и магнитный и электрический поток. При этом, как в магнитном, так и в электрическом поле накопленная энергия возрастает. Когда волна начинает двигаться в обратном направлении, то электрическое поле начинает исчезать, а его энергия переходит в магнитную энергию обратной волны тока. После того, как фронт волны напряжения достигает входа линии, магнитное поле и ток в ней удваивается, а электрическое поле исчезает. Далее цикл повторяется. Следовательно, процессу возрастания магнитного потока в индуктивности закороченной длинной линия, в обязательном порядке сопутствует процесс периодического изменения потока электрической индукции, в результате чего между плоскостями линии периодически возникает и исчезает электрическое поле.
Допустим, что линия выполнена из сверхпроводника и не имеет потерь. Тогда заменив в определённый момент генератор напряжения сверхпроводящей перемычкой, можно заморозить ток в линии. Наиболее благоприятным моментом для такой процедуры является момент, когда в линии полностью отсутствует электрическое поле. Тогда в линии будет заморожен поток  , которому будет соответствовать ток
, которому будет соответствовать ток  . Что будет, если замену источника напряжения сверхпроводящей перемычкой произвести в тот момент времени, когда в линии находится фронт напряжения и какой-то её участок заполнен электрическими полями? В этом случае этот участок будет двигаться в линии, попеременно отражаясь то от одного, то от другого конца закороченной линии, пока не истратит свою энергию на излучение. По этой причине в закороченной с обеих сторон линии может быть заморожено только целочисленное (квантованное) значение потока и тока в соответствии с приведенными соотношениями.
. Что будет, если замену источника напряжения сверхпроводящей перемычкой произвести в тот момент времени, когда в линии находится фронт напряжения и какой-то её участок заполнен электрическими полями? В этом случае этот участок будет двигаться в линии, попеременно отражаясь то от одного, то от другого конца закороченной линии, пока не истратит свою энергию на излучение. По этой причине в закороченной с обеих сторон линии может быть заморожено только целочисленное (квантованное) значение потока и тока в соответствии с приведенными соотношениями.
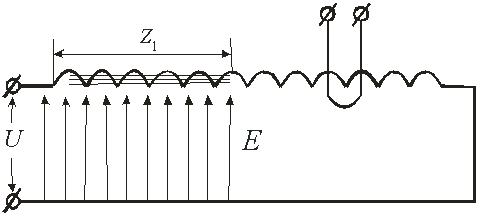
Это явление является примером макроскопического квантования потока в макроскопических структурах, имеющих определённые размеры. Такое же квантование потока происходит и в микроскопических структурах, которыми являются атомы. С точки зрения цепей с сосредоточенными параметрами, нарастание тока в соленоиде при подключении к нему источника напряжения происходит по линейному закону, причём во всех его витках одновременно. Но так ли это? Для выяснения этого вопроса заменим верхнюю плоскость рассмотренной двухпроводной линии (рис. 8) длинным соленоидом. Если к такой линии подключить источник напряжения, то процесс нарастания тока в ней ничем не будет отличаться от рассмотренного. Погонная индуктивность линии будет теперь в основном определяться погонной индуктивностью соленоида и скорость распространения и волны тока, и волны напряжения (напряжение теперь будет приложено между соленоидом и нижним проводником линии) будет меньше, чем в предыдущем случае.
Когда в рассмотренной линии волна дойдет до точки с координатой ![]() , то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой
, то магнитным полем будет заполнена только часть соленоида, расположенная между источником питания и точкой ![]() . Когда волна дойдет до его конца, то магнитным полем будет заполнен весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, внутренний магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида.
. Когда волна дойдет до его конца, то магнитным полем будет заполнен весь соленоид. При обратном ходе волны магнитное поле в соленоиде удвоится, и процесс начнется сначала. Таким образом, внутренний магнитный поток в любом поперечном сечении соленоида будет нарастать не плавно, а скачками, и период этих скачков будет определяться временем прохождения волной данного закороченного отрезка соленоида.
Рис. 8. Схема распространения магнитных и электрических полей в длинном соленоиде.
Положим теперь, что соленоид в определенном месте охвачен витком.
Этот процесс подобен механическому одеванию охватывающего витка на конец соленоида с той лишь разницей, что в данном случае магнитный поток, перемещаясь внутри соленоида, сам пронизывает охватывающий его виток. Причём скорость движения фронта магнитного потока при этом несоизмеримо больше, чем при механическом одевании. Но оба процесса имеют одинаковую природу. Этими процессами и объясняется явление взаимной индукции между соленоидом и охватывающим витком. При небольшой длине соленоида расстояние между импульсами невелико, поэтому они, сливаясь, образуют почти постоянное напряжение. Напряжение в витке будет индуцироваться только в момент пересечения магнитным потоком соленоида окрестностей поперечного сечения, охваченного витком. В этот момент в окрестностях охватывающего витка будет возникать, как векторный потенциал, так и магнитное поле. И, именно, пересечение охватывающего витка магнитными полями рассеяния (такого же, как и на конце соленоида с постоянным током) приводит к индуцированию в нём э.д.с. Этот момент будет наступать как при прямом, так и при обратном ходе волны, причем полярность импульсов напряжения, индуцируемых в витке, в обоих случаях будет одна и та же. Частота этих импульсов будет зависеть от длины соленоида, и будет тем больше, чем короче соленоид. Следовательно, среднее значение индуцированного напряжения будет расти с уменьшением длины соленоида, т.е. его количества витков, что и определяет коэффициент трансформации такого трансформатора, который равен отношению количества витков соленоида и охватывающей обмотки.
Рассмотрев процесс нарастания токов и полей в длинном соленоиде, вернёмся к вопросу о наличии циркуляции векторного потенциала вокруг длинного соленоида. Приведём существующую точку зрения по этому вопросу, представленную в работе [1]. Значение векторного потенциала в пространстве, окружающем соленоид, находится из соотношения
(2.6)
где ![]() - количество витков, приходящееся на единицу длины соленоида,
- количество витков, приходящееся на единицу длины соленоида, ![]() - ток, текущий через соленоид,
- ток, текущий через соленоид, ![]() - диаметр соленоида,
- диаметр соленоида, ![]() - расстояние от оси соленоида до точки наблюдения.
- расстояние от оси соленоида до точки наблюдения.
При записи этого соотношения предполагается, что ![]() .
.
Индуктивность соленоида определяется выражением
(2.7)
Если к соленоиду подключить источник постоянного напряжения ![]() , то с учётом соотношений (2.5 -2.7), получаем
, то с учётом соотношений (2.5 -2.7), получаем
где ![]() - общее число витков в соленоиде, а поскольку
- общее число витков в соленоиде, а поскольку
то напряжённость электрического поля в окрестности соленоида в момент подключения к нему источника постоянного напряжения составит
Указанная напряжённость электрического поля в соответствии с рассматриваемой версией возникает в момент подключения к соленоиду источника питания мгновенно на всём его протяжении. Если у соленоида отсутствует сопротивление, то напряжённость электрического поля будет неизменной за весь период времени подключения к соленоиду источника постоянного напряжения. Какие здесь возникают противоречия? Во-первых, электрические поля обладают энергией, и возникать мгновенно не могут. Второе противоречие вытекает из первого и заключается в том, что, поскольку электрические поля обладают энергией, то эта энергия должна включаться в общую энергию, накопленную в соленоиде. Но при расчёте такой энергии учитываются только магнитные поля внутри соленоида.
Таким образом, сам процесс индукции электрических полей вокруг длинного соленоида происходит совсем не так, как это представлено в существующей литературе [1], когда считается, что циркуляция магнитного векторного потенциала на всём его протяжении возрастает одновременно, что и приводит к индукции э.д.с. в охватывающем витке.
Из сказанного можно заключить, что точка зрения о возникновении электрических полей индукции вокруг соленоида в том месте, где ротор векторного потенциала равен нулю, не соответствует действительности, а сам процесс формирования векторного потенциала снаружи соленоида и магнитных полей внутри него не соответствует тем представлениям, которые существуют на сегодняшний день. Ротор векторного потенциала снаружи соленоида равен нулю, и такое поле не обладает никакой энергией, поэтому и обнаружить его в статическом режиме не представляется возможным. По этой причине эксперименты Аронова и Бома по обнаружению векторного потенциала снаружи длинного соленоида, в качестве которого использовался намагниченный ферромагнитный цилиндрический образец малого диаметра, следует считать ошибочными.
Рассмотрим диаграмму распространения тока и напряжения в отрезке длинной линии, представленной на рис. 4. На этом рисунке сам фронт волны показан скошенным и занимает отрезок линии длинной ![]() , следовательно, время такого переходного процесса равно
, следовательно, время такого переходного процесса равно  . Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время
. Это как раз то время, за которое напряжение на входе линии вырастает от нуля до своего номинального значения. Длительность данного переходного процесса является регулируемой, и зависит от того, по какому закону мы увеличиваем напряжение на входе линии, Сейчас мы попытаемся понять, откуда берется та напряженность поля, которая заставляет заряды в проводниках, расположенных вблизи токонесущих элементов линии, двигаться в направлении противоположном направлению движения зарядов в первичной (индуцирующей) линии. Это как раз тот вопрос, на который до сих пор нет физического ответа. Предположим, что напряжение на входе линии возрастает по линейному закону и за время ![]() достигает своего максимального значения
достигает своего максимального значения ![]() , после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок
, после чего его рост прекращается. Тогда в самой линии переходной процесс займет участок ![]() . Изобразим этот участок отдельно, как показано на рис. 9.
. Изобразим этот участок отдельно, как показано на рис. 9.
Рис. 9. Фронт волны тока, распространяющейся в длинной линии
На участке ![]() происходит ускорение зарядов от их нулевой скорости (правее участка
происходит ускорение зарядов от их нулевой скорости (правее участка ![]() ) до значения скорости, определяемого соотношением
) до значения скорости, определяемого соотношением
где ![]() и
и ![]() - заряд и масса носителей тока, а
- заряд и масса носителей тока, а ![]() - падение напряжения на участке
- падение напряжения на участке ![]() . Тогда зависимость скорости носителей тока от координаты будет иметь вид:
. Тогда зависимость скорости носителей тока от координаты будет иметь вид:
(2.8)
Поскольку мы приняли линейную зависимость напряжения от времени на входе линии, то имеет место равенство
где ![]() - напряженность поля, ускоряющая заряды на участке
- напряженность поля, ускоряющая заряды на участке ![]() . Следовательно, соотношение (2.8) мы можем переписать
. Следовательно, соотношение (2.8) мы можем переписать
Теперь, используя соотношение (2.4) для величины скалярно-векторного потенциала, вычислим его значение как функцию ![]() на некотором расстоянии
на некотором расстоянии ![]() от линии
от линии
(2.9)
При записи соотношения (2.9) использованы только первые два члена разложения в ряд, функции, определяемой соотношением (2.4).
Пользуясь формулой ![]() , и продифференцировав соотношение (2.9) по
, и продифференцировав соотношение (2.9) по ![]() , получаем
, получаем
(2.10)
где ![]() - электрическое поле, индуцируемое на расстоянии
- электрическое поле, индуцируемое на расстоянии ![]() от проводника линии. Около
от проводника линии. Около ![]() мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружающих линию проводниках индукционные токи, противоположные по направлению тем, которые текут в индуцирующей линии. Ускорение
мы поставили штрих в связи с тем, что вычисленное поле движется вдоль проводника линии со скоростью света, индуцируя в окружающих линию проводниках индукционные токи, противоположные по направлению тем, которые текут в индуцирующей линии. Ускорение ![]() , испытуемое зарядом
, испытуемое зарядом ![]() в поле
в поле ![]() , определяется соотношением
, определяется соотношением  . С учетом этого из (2.10) получаем
. С учетом этого из (2.10) получаем
(2.11)
Таким образом, заряды, ускоряемые в отрезке линии ![]() , индуцируют на расстоянии
, индуцируют на расстоянии ![]() от этого участка электрическое поле, определяемое соотношением (2.11). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Таким образом, получен закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Этот закон можно называть законом электро-электрической индукции, так как он, минуя поля посредники (магнитное поле или векторный потенциал), дает прямой ответ на то, какие электрические поля генерирует вокруг себя ускоряемый электрический заряд. Данный закон дает также ответ о месте приложения сил взаимодействия между зарядами. Именно это соотношение, а не закон Фарадея, мы должны считать основным законом индукции, т.к. именно оно устанавливает причину появления индукционных электрических полей вокруг движущегося заряда. В чем заключается разница между предлагаемым подходом и ранее существующим. Ранее говорилось, что движущийся заряд генерирует векторный потенциал, а уже изменяющийся векторный потенциал генерирует электрическое поле. Соотношение (2.11) дает возможность исключить эту промежуточную операцию и перейти непосредственно от свойств движущегося заряда к индукционным полям. Из соотношению (2.11) следует и введенный ранее феноменологическим путем векторный потенциал, а, следовательно, и магнитное поле. Равенство (2.11) можно переписать
от этого участка электрическое поле, определяемое соотношением (2.11). Направление этого поля обратно полю, приложенного к ускоряемым зарядам. Таким образом, получен закон прямого действия, который указывает на то, какие электрические поля вокруг себя генерирует ускоряемый заряд. Этот закон можно называть законом электро-электрической индукции, так как он, минуя поля посредники (магнитное поле или векторный потенциал), дает прямой ответ на то, какие электрические поля генерирует вокруг себя ускоряемый электрический заряд. Данный закон дает также ответ о месте приложения сил взаимодействия между зарядами. Именно это соотношение, а не закон Фарадея, мы должны считать основным законом индукции, т.к. именно оно устанавливает причину появления индукционных электрических полей вокруг движущегося заряда. В чем заключается разница между предлагаемым подходом и ранее существующим. Ранее говорилось, что движущийся заряд генерирует векторный потенциал, а уже изменяющийся векторный потенциал генерирует электрическое поле. Соотношение (2.11) дает возможность исключить эту промежуточную операцию и перейти непосредственно от свойств движущегося заряда к индукционным полям. Из соотношению (2.11) следует и введенный ранее феноменологическим путем векторный потенциал, а, следовательно, и магнитное поле. Равенство (2.11) можно переписать
откуда, интегрируя по времени, получаем
Это соотношение полностью соответствует определению векторного потенциала. Теперь видно, что векторный потенциал есть прямое следствие зависимости скалярного потенциала от скорости. Введение и векторного потенциала и магнитного поля это всего лишь полезный математический приём, который позволяет упростить решение ряда электродинамических задач, однако, следует помнить, что первоосновой введение этих полей является скалярно-векторный потенциал.
Новые подходы к вопросу силового взаимодействия токонесущих систем
Но векторный потенциал определяет не только электрические поля, индуцируемые ускоряемыми электрическими зарядами, но и силовое взаимодействие проводников, по которым текут токи, а также силовое взаимодействие движущихся зарядов с такими проводниками.
С точки зрения существующей теории электромагнетизма силы взаимодействия проводников можно найти двумя путями.
Первый из них заключается в том, что один из проводников (например, нижний) создает в месте расположения верхнего проводника магнитное поле H(r), которое определяется соотношением
Рис. 10. Схема силового взаимодействия токонесущих проводов двухпроводной линии на основе существующей модели.
В системе координат, двигающейся вместе с зарядами верхнего проводника, возникает поле ![]() , определяемое соотношением
, определяемое соотношением
т.е. заряды, двигающиеся в верхнем проводнике, испытывают действие силы Лоренца. Значение этой силы, приходящейся на единицу длины проводника, записывается как:
Это соотношение можно получить и другим путем. Можно считать, что нижний проводник создает в районе расположения верхней проволоки векторный потенциал, z – компонента которого запишется
Потенциальная энергия единичного участка верхнего проводника, по которому течет ток ![]() , в поле векторного потенциала
, в поле векторного потенциала ![]() определятся соотношением
определятся соотношением
Поскольку сила определяется как производная потенциальной энергии по координате, взятая с обратным знаком, то она запишется
Оба рассмотрения показывают, что сила взаимодействия двух проводников возникает как результат взаимодействия движущихся зарядов, т.к. одни из них создают поля, а другие с этими полями взаимодействуют. Неподвижные заряды, представляющие решетку, в такой схеме взаимодействия участия не принимают. Однако, силы, возникающие при магнитном взаимодействии проводников, приложены именно к решетке. Вопрос о том, каким образом движущиеся заряды передают приложенные к ним силы решетке, в классической электродинамике не рассматривается.
Отметим также, что рассмотренные схемы взаимодействия заключают в себе одно неразрешимое противоречие, которое специалисты по классической электродинамике обычно умалчивают. Оно связано с нахождением сил взаимодействия между двумя параллельно движущимися зарядами. С точки зрения рассмотренных схем, между такими двумя зарядами должно существовать притяжение. Действительно, индукция В, создаваемая движущимся зарядом ![]() на расстоянии r от него, записывается
на расстоянии r от него, записывается
Если имеется другой заряд g2, двигающийся с той же скоростью V, что и первый и в том же направлении на расстоянии r от первого заряда, то за счет наличия в этой точке индукции ![]() на него будет действовать сила притяжения к первому заряду
на него будет действовать сила притяжения к первому заряду
Т.е. с точки зрения неподвижного наблюдателя такие заряды, кроме наличия сил кулоновского отталкивания должны дополнительно притягиваться. С точки же зрения наблюдателя, двигающегося вместе с зарядами, имеется только кулоновское отталкивание и никаких дополнительных сил притяжения нет. Отметим, что данное противоречие неразрешимо не только в рамках классической электродинамики, но и в рамках специальной теории относительности.
С физической точки зрения введение магнитных полей есть просто констатация определенных экспериментальных фактов, однако, мы до сих пор не понимаем, откуда эти поля берутся.
Концепция магнитного поля возникла в значительной степени благодаря наблюдениям за силовым взаимодействием токонесущих и намагниченных систем. Особенно показательным является опыт с железными опилками, которые выстраиваются около полюсов магнита или вокруг кольцевого витка с током в чёткие геометрические фигуры. Эти фигуры и послужили поводом для введения такого понятия, как силовые линии. При любом силовом взаимодействии, в соответствии с третьим законом Ньютона, всегда существует равенство сил действия и противодействия, а также всегда имеются те элементы системы, к которым эти силы приложены. Большим недостатком концепции магнитного поля является то, что она не даёт ответа на то, куда конкретно приложены силы действия и противодействия, т.к. магнитное поле выступает как самостоятельная субстанция, с которой и происходит взаимодействие движущихся зарядов.
Экспериментально известно, что силы взаимодействия в токонесущих системах приложены к тем проводникам, движущиеся заряды которых создают магнитное поле. Однако в существующей концепции силового взаимодействия токонесущих систем, основанной на понятиях магнитного поля и силы Лоренца, положительно заряженная решетка, которая является остовом проводника и к которой приложены силы, не участвует в формировании сил взаимодействия. То, что положительно заряженные ионы принимают непосредственное участие в силовых процессах, говорит уже, хотя бы, тот факт, что в процессе сжатия плазмы, при протекании через нее постоянного тока происходит сжатие и ионов (так называемый пинч-эффект).
Рассмотрим этот вопрос на основе концепции скалярно-векторного потенциала. Будем считать, что скалярно-векторный потенциал одиночного заряда определяется соотношением (2.4), и что электрические поля, создаваемые этим потенциалом, действуют на все окружающие заряды, в том числе и на заряды положительно заряженной решетки.
Разберем с этих позиций силовое взаимодействие между двумя параллельными проводниками (рис. 11), по которым протекают токи. Будем считать, что ![]() ,
, ![]() и
и ![]() ,
, ![]() представляют соответственно неподвижные и движущиеся заряды, приходящиеся на единицу длины проводника.
представляют соответственно неподвижные и движущиеся заряды, приходящиеся на единицу длины проводника.
Рис. 11. Схема силового взаимодействия токонесущих проводов двухпроводной линии с учетом положительно заряженной решетки.
Заряды ![]() ,
, ![]() представляют положительно заряженную решетку в нижнем и верхнем проводниках. Будем также считать, что оба проводника до начала движения зарядов являются электронейтральными, т.е. в проводниках имеется две системы взаимно вложенных разноименных зарядов с удельной плотностью на
представляют положительно заряженную решетку в нижнем и верхнем проводниках. Будем также считать, что оба проводника до начала движения зарядов являются электронейтральными, т.е. в проводниках имеется две системы взаимно вложенных разноименных зарядов с удельной плотностью на ![]() ,
, ![]() и
и ![]() ,
, ![]() , которые электрически нейтрализуют друг друга. На рис. 11 эти системы для большего удобства рассмотрения сил взаимодействия раздвинуты по оси z. Подсистемы с отрицательным зарядом (электроны) могут двигаться со скоростями
, которые электрически нейтрализуют друг друга. На рис. 11 эти системы для большего удобства рассмотрения сил взаимодействия раздвинуты по оси z. Подсистемы с отрицательным зарядом (электроны) могут двигаться со скоростями ![]() и
и ![]() . Силу взаимодействия между нижним и верхним проводниками будем искать как сумму четырех сил, обозначение которых понятно из рисунка. Силы отталкивания
. Силу взаимодействия между нижним и верхним проводниками будем искать как сумму четырех сил, обозначение которых понятно из рисунка. Силы отталкивания ![]() и
и ![]() будем брать со знаком минус, а силы притяжения
будем брать со знаком минус, а силы притяжения ![]() и
и ![]() будем брать со знаком плюс.
будем брать со знаком плюс.
Для единичного участка двухпроводной линии силы, действующие между отдельными подсистемами, запишутся
(3.1)
Складывая все силы, получим величину суммарной силы, приходящейся на единицу длины проводника,
(3.2)
В данном выражении в качестве ![]() и
и ![]() взяты абсолютные величины зарядов, а знаки сил учтены в выражении в скобках. Для случая
взяты абсолютные величины зарядов, а знаки сил учтены в выражении в скобках. Для случая ![]() <<
<< ![]() , возьмем только два первых члена разложения в ряд
, возьмем только два первых члена разложения в ряд ![]() , т.е. будем считать, что
, т.е. будем считать, что  . Из соотношения (20.2) получаем
. Из соотношения (20.2) получаем
(3.3)
где в качестве ![]() и
и ![]() взяты абсолютные величины удельных зарядов, а
взяты абсолютные величины удельных зарядов, а ![]() и
и ![]() берут со своими знаками.
берут со своими знаками.
Поскольку магнитное поле прямого провода, по которому течёт ток ![]() , определяем соотношением
, определяем соотношением
то из соотношения (3.3) получаем:
где ![]() - магнитное поле создаваемое нижним проводником, по которому течёт ток
- магнитное поле создаваемое нижним проводником, по которому течёт ток ![]() , в месте расположения верхнего проводника.
, в месте расположения верхнего проводника.
Аналогично
где ![]() - магнитное поле, создаваемое верхним проводником в районе расположения нижнего проводника.
- магнитное поле, создаваемое верхним проводником в районе расположения нижнего проводника.
Эти соотношения полностью совпадают с результатами, полученными на основании концепции магнитного поля.
Соотношение (3.3) представляет известное правило силового взаимодействия токонесущих систем, но получено оно не феноменологическим путем на основании введения феноменологического магнитного поля, а на основе вполне понятных физических процедур, в предположении того, что скалярный потенциал заряда зависит от скорости. В формировании сил взаимодействия в данном случае непосредственное участие принимает решетка, чего нет в модели магнитного поля. В рассмотренной модели хорошо видны места приложения сил. Полученные соотношения совпадают с результатами, полученными на основе концепции магнитного поля и аксиоматически введённой силой Лоренца. В данном случае взят только первый член разложения в ряд ![]() . Для скоростей
. Для скоростей ![]() ~
~ ![]() следует брать все члены разложения. Этим предлагаемый метод отличается от метода расчёта силовых взаимодействий на основе концепции магнитного поля. Если учесть это обстоятельство, то связь между силами взаимодействия и скоростями зарядов оказывается нелинейной. Это, в частности приводит к тому, что закон силового взаимодействия токонесущих систем является асимметричным. При одинаковых значениях токов, но при разных их направлениях, силы притяжения и отталкивания становятся неодинаковыми. Силы отталкивания оказываются большими, чем силы притяжения. Эта разница невелика и определяется выражением
следует брать все члены разложения. Этим предлагаемый метод отличается от метода расчёта силовых взаимодействий на основе концепции магнитного поля. Если учесть это обстоятельство, то связь между силами взаимодействия и скоростями зарядов оказывается нелинейной. Это, в частности приводит к тому, что закон силового взаимодействия токонесущих систем является асимметричным. При одинаковых значениях токов, но при разных их направлениях, силы притяжения и отталкивания становятся неодинаковыми. Силы отталкивания оказываются большими, чем силы притяжения. Эта разница невелика и определяется выражением
но при скоростях носителей зарядов близких к скорости света она может оказаться вполне ощутимой.
Уберем решетку верхнего проводника (рис. 11), оставив только свободный электронный поток. При этом исчезнут силы ![]() и
и ![]() , и это будет означать взаимодействие нижнего проводника с потоком свободных электронов, движущихся со скоростью
, и это будет означать взаимодействие нижнего проводника с потоком свободных электронов, движущихся со скоростью ![]() на месте расположения верхнего проводника. При этом значение силы взаимодействия определяется как:
на месте расположения верхнего проводника. При этом значение силы взаимодействия определяется как:
(3.4)
Сила Лоренца предполагает линейную зависимость между силой, действующей на заряд, движущийся в магнитном поле, и его скоростью. Однако в полученном соотношении зависимость величины силы от скорости электронного потока будет нелинейной. Из соотношения (3.4) нетрудно видеть, что с ростом ![]() отклонение от линейного закона увеличивается, и в случае, когда
отклонение от линейного закона увеличивается, и в случае, когда ![]() >>
>> ![]() , сила взаимодействия стремятся к нулю. Это очень важный результат. Именно этот феномен и наблюдали в своих известных экспериментах Томпсон и Кауфман, когда заметили, что с ростом скорости электронного пучка он хуже отклоняется магнитным полем. Результаты своих наблюдений они связали с ростом массы электрона. Как видим причина здесь другая.
, сила взаимодействия стремятся к нулю. Это очень важный результат. Именно этот феномен и наблюдали в своих известных экспериментах Томпсон и Кауфман, когда заметили, что с ростом скорости электронного пучка он хуже отклоняется магнитным полем. Результаты своих наблюдений они связали с ростом массы электрона. Как видим причина здесь другая.
Отметим ещё один интересный результат. Из соотношения (3.3), с точностью до квадратичных членов, сила взаимодействия электронного потока с прямолинейным проводником, по которому протекает ток, можно определить по следующей зависимости:
(3.5)
Из выражения (3.5) следует, что при однонаправленном движении электронов в проводнике и в электронном потоке сила взаимодействия при выполнении условия  отсутствует.
отсутствует.
Поскольку скорость электронного потока обычно гораздо выше скорости носителей тока в проводнике, то вторым членом в скобках в соотношении (3.5) можно пренебречь. Тогда, поскольку
магнитное поле, создаваемое нижним проводником в месте движения электронного потока, получим:
В данном случае, полученное значение силы в точности совпадает со значением силы Лоренца.
Учитывая, что
можно считать, что на заряд, движущийся в магнитном поле, действует электрическое поле ![]() , направленное нормально к направлению движения заряда. Данный результат также с точностью до квадратичных членов
, направленное нормально к направлению движения заряда. Данный результат также с точностью до квадратичных членов ![]() полностью совпадает с результатами концепции магнитного поля и определяет силу Лоренца, действующую со стороны магнитного поля на поток движущихся электронов.
полностью совпадает с результатами концепции магнитного поля и определяет силу Лоренца, действующую со стороны магнитного поля на поток движущихся электронов.
Как уже было сказано, одним из важных противоречий концепции магнитного поля является то, что два параллельных пучка одноименных зарядов, двигающихся с одинаковой скоростью в одном направлении, должны притягиваться. В данной модели этого противоречия уже нет. Если считать, что скорости зарядов в верхнем и нижнем проводе будут равны, а решетка отсутствует, т.е. оставить только электронные потоки, то останется только сила отталкивания ![]() независимо от того движутся заряды или нет.
независимо от того движутся заряды или нет.
Таким образом, движущийся электронный поток взаимодействует одновременно и с движущимися электронами в нижней проволоке, и с её решеткой, а сумма этих сил взаимодействия и называется силой Лоренца. Эта сила и действует на движущийся поток электронов.
Закономерно возникает вопрос, а создаёт ли магнитное поле сам движущийся поток электронов в отсутствии компенсирующих зарядов решетки или положительных ионов в плазме? Рассмотренная схема показывает, что эффект силового взаимодействия между токонесущими системами требует в обязательном порядке наличия положительно заряженной решетки. Поэтому сам движущийся электронный поток не может создавать того эффекта, который создаётся при его движении в положительно заряженной решетке. В то же время, если рассмотреть два параллельно движущихся потока электронов, то возникает дополнительная сила взаимодействия, зависящая от относительной скорости этих потоков.
Продемонстрируем ещё один подход к проблеме силового взаимодействия токонесущих систем. Констатация факта наличия сил между токонесущими системами указывает на то, что существует какое-то поле скалярного потенциала, градиент которого и обеспечивает указанную силу. Но что это за поле? Соотношение (3.3) даёт только значение силы, но не говорит о том, градиент какого скалярного потенциала эти силы обеспечивает. Будем поддерживать постоянными токи ![]() и
и ![]() , и начнём сближать или удалять проводники. Работа, которая при этом будет затрачена, и есть тот потенциал, градиент которого даёт силу. Проинтегрировав соотношение (3.3) по
, и начнём сближать или удалять проводники. Работа, которая при этом будет затрачена, и есть тот потенциал, градиент которого даёт силу. Проинтегрировав соотношение (3.3) по ![]() , получаем величину энергии:
, получаем величину энергии:
Эта энергия, в зависимости от того удалять проводники друг от друга, или сближать, может быть положительной или отрицательной. Когда проводники удаляют, то энергия положительна, а это означает, что, поддерживая ток в проводниках постоянным, генератор отдаёт энергию. Это явление и лежит в основе работы всех электродвигателей. Если проводники сближаются, то работу совершают внешние силы, над источником, поддерживающим в них постоянство токов. Это явление лежит в основе работы механических генераторов э.д.с.
Соотношение для энергии можно переписать и так:
где
есть ![]() - компонента векторного потенциала, создаваемая нижним проводником в месте расположения верхнего проводника, а
- компонента векторного потенциала, создаваемая нижним проводником в месте расположения верхнего проводника, а
есть ![]() - компонента векторного потенциала, создаваемая верхним проводником в месте расположения нижнего проводника.
- компонента векторного потенциала, создаваемая верхним проводником в месте расположения нижнего проводника.
Рассмотренный подход демонстрирует ту большую роль, которую играет векторный потенциал в вопросах силового взаимодействия токонесущих систем и преобразования электрической энергии в механическую. Такой подход также ясно указывает на то, что сила Лоренца есть следствие взаимодействия токонесущих систем с полем векторного потенциала, создаваемого другими токонесущими системами. И важным обстоятельством является то, что формирование векторного потенциала обязано зависимости скалярного потенциала от скорости. С физической точки зрения это ясно. Движущиеся заряды, в связи с наличием зависимости их скалярного потенциала от скорости, создают скалярное поле, градиент которого и даёт силу. Но создание любого силового поля требует затрат энергии. Эти затраты и совершает генератор, создавая токи в проводниках. При этом в окружающем пространстве создаётся особое поле, которое взаимодействует с другими движущимися зарядами по особым векторным правилам, при которых только скалярное произведение вектора скорости заряда и векторного потенциала даёт потенциал, градиент которого и даёт силу, действующую на движущийся заряд. Это и есть сила Лоренца.
Несмотря на простоту и очевидность такого подхода, этот простой механизм до настоящего времени не был окончательно осознан. По этой причине сила Лоренца до сих пор вводилась в классической электродинамике аксиоматическим путём.
Рассмотрим ещё один случай, когда одиночный отрицательный заряд ![]() движется со скоростью
движется со скоростью ![]() параллельно проводнику, по которому со скоростью
параллельно проводнику, по которому со скоростью ![]() двигаются электроны, удельная плотность которых, приходящаяся на единицу длины провода, составляет
двигаются электроны, удельная плотность которых, приходящаяся на единицу длины провода, составляет ![]() (рис.12). Будем считать, что проводник до начала движения электронов был электронейтральным и удельная плотность положительных ионов и электронов были равны. Элемент заряда, приходящийся на отрезок
(рис.12). Будем считать, что проводник до начала движения электронов был электронейтральным и удельная плотность положительных ионов и электронов были равны. Элемент заряда, приходящийся на отрезок ![]() проводника с током, при этом составит
проводника с током, при этом составит ![]() . Элемент силы действия движущегося заряда
. Элемент силы действия движущегося заряда ![]() на элемент
на элемент ![]() определится соотношением:
определится соотношением:
где ![]() и
и ![]() - компоненты соответствующих скоростей, нормальные к радиусу, соединяющему движущийся заряд с элементом заряда
- компоненты соответствующих скоростей, нормальные к радиусу, соединяющему движущийся заряд с элементом заряда ![]() .
.
Поскольку ![]() и
и ![]() , а также, учитывая, что
, а также, учитывая, что ![]() и
и  , можно записать:
, можно записать:
Рис. 12. Схема взаимодействия движущегося точечного заряда с проводником, по которому течёт ток.
Полученная сила - это сила притяжения. Элемент этой силы, параллельной , запишется как:
(3.6)
а элемент силы, нормальной к ![]() - как:
- как:
(3.7)
Проинтегрировав соотношение (3.6) и учитывая, что ток, текущий по нижнему проводнику определяется соотношением ![]() , запишем силу, действующую на одиночный движущийся заряд
, запишем силу, действующую на одиночный движущийся заряд ![]() со стороны правой части проволоки:
со стороны правой части проволоки:
(3.8)
Если учесть также взаимодействие с левой её частью проволоки, то сила, действующая параллельно ![]() и определяемая соотношением (3.8), удвоится, а силы, действующие по нормали к
и определяемая соотношением (3.8), удвоится, а силы, действующие по нормали к ![]() , компенсируются. Таким образом, суммарная сила, действующая на заряд, движущийся параллельно проволоке, запишется:
, компенсируются. Таким образом, суммарная сила, действующая на заряд, движущийся параллельно проволоке, запишется:
(3.9)
Поскольку магнитное поле, создаваемое нижним проводником с током в точке нахождения движущегося заряда, определяется соотношением

а магнитная проницаемость 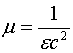 , то из соотношения (3.8) получаем
, то из соотношения (3.8) получаем
![]()
Эта сила в точности равна силе Лоренца.
Теперь рассмотрим случай, когда заряд движется между двумя безграничными параллельными пластинами, по которым протекает удельный ток ![]() , приходящийся на единицу ширины пластин (рис. 13). Этот ток течёт по нормали к плоскости рисунка. При этом заряд движется параллельно току, протекающему в пластинах.
, приходящийся на единицу ширины пластин (рис. 13). Этот ток течёт по нормали к плоскости рисунка. При этом заряд движется параллельно току, протекающему в пластинах.
Рис.13. Схема взаимодействия движущегося точечного заряда с токами, текущими по параллельным проводящим пластинам.
Учитывая соотношение (3.9), запишем элемент силы, действующей на движущийся заряд со стороны элемента тока, текущего нормально к элементу ![]()
(3.10)
В этом соотношении ![]() это толщина слоя, по которому течёт ток, а
это толщина слоя, по которому течёт ток, а ![]() - плотность электронов.
- плотность электронов.
Перепишем соотношение (3.10), учитывая что  ,
,  , а также то, что
, а также то, что 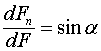 , где
, где ![]() - элемент силы, направленный параллельно
- элемент силы, направленный параллельно ![]() , а
, а ![]() - элемент силы, направленный нормально к
- элемент силы, направленный нормально к ![]() :
:
Проинтегрировав это выражение, получим полную силу, действующую на движущийся заряд со стороны одной полуплоскости:
Учитывая, что в случае, когда элемент ![]() равен единичной длине, выполняется соотношение
равен единичной длине, выполняется соотношение ![]() , а также то, что на заряд действуют силы со стороны четырёх полуплоскостей (две со стороны нижней пластины и две со стороны верхней), окончательно получаем:
, а также то, что на заряд действуют силы со стороны четырёх полуплоскостей (две со стороны нижней пластины и две со стороны верхней), окончательно получаем:
И опять конечный результат в точности совпал с результатами концепции магнитного поля.
Таким образом, результаты, полученные с учётом введения скалярно-векторного потенциала и концепции магнитного поля, полностью совпадают, если учитывать только квадратичные члены разложения гиперболического косинуса в ряд. В случае учёта членов разложения более высоких порядков, когда скорости движения зарядов велики, такого совпадения не будет и связь между силой и скоростью становится нелинейной, и концепция магнитного поля уже не даст правильных результатов.
Достоинством данного метода рассмотрения взаимодействия между токонесущими системами и зарядами является то, что он указывает на конкретные места приложения сил, действующих между их элементами и движущимися зарядами, чего нет в концепции магнитного поля. Рассмотренный подход даёт возможность определить силы взаимодействия между любыми токонесущими системами при любой их конфигурации, и показывает, что такие понятия, как магнитный векторный потенциал и магнитное поле для стационарных процессов это следствие зависимости скалярного потенциала заряда от скорости его движения. В случае же нестационарных процессов, когда возникает ускорение заряда, при решении задачи следует учитывать эффекты запаздывания.
Список Литературы
- 1. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М: Мир, 1977.
- 2. Мандельштам Л. И. Лекции по оптике, теории относительности и квантовой механике. М: Наука, 1972. – 437 с.
- 3. Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967, - 664 - с.
- 4. Менде Ф. Ф. К вопросу об уточнении уравнений электромагнитной индукции. - Харьков, депонирована в ВИНИТИ, №774-В88 Деп., 1988.-32с.
- 5. Менде Ф. Ф. Существуют ли ошибки в современной физике. Харьков, Константа, 2003.- 72 с.
- 6. Менде Ф. Ф. Непротиворечивая электродинамика. Харьков, НТМТ, 2008, – 153 с. ISBN 978-966-8603-23-5.
- 7. Менде Ф. Ф. Великие заблуждения и ошибки физиков XIX-XX столетий. Революция в современной физике.. Харьков, НТМТ, 2010, – 176 с. ISBN 978-617-578-010-7.